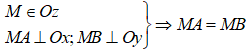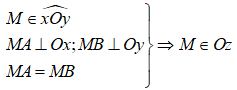Toán 7 Chương 3 Bài 5: Tính chất tia phân giác của một góc
Mời các em cùng tham khảo nội dung bài giảng dưới đây do eLib tổng hợp và biên soạn. Bài học sẽ giới thiệu đến các em kiến thức về Tính chất tia phân giác của một góc cùng với những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng nắm đươc nội dung phần này.
Mục lục nội dung

Toán 7 Chương 3 Bài 5: Tính chất tia phân giác của một góc
1. Tóm tắt lý thuyết
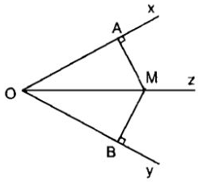
1.1. Định lý 1 (định lý thuận)
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ví dụ: Ta có:
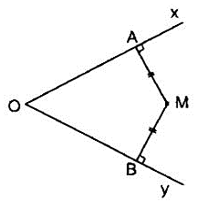
1.2. Định lý 2 (định lý đảo)
Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Ví dụ: Ta có:
Nhận xét: Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
2. Bài tập minh họa
Câu 1: Các phân giác ngoài của ΔABC cắt nhau tạo thành ΔEFG.
a) Tính các góc của ΔEFG theo các góc của ΔABC
b) Chứng minh các phân giác trong của ΔABC đi qua các đỉnh E, F, G.
Hướng dẫn giải
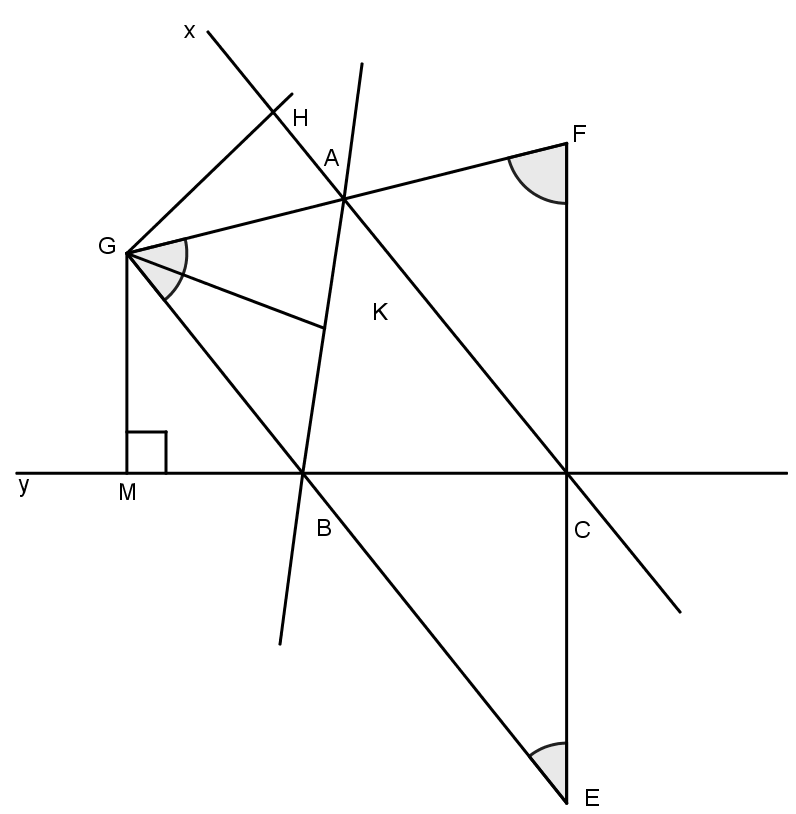
a) Kí hiệu như hình vẽ:
Trong ΔGAB có: ˆG=1800−12(^xAB+^yBA)
Mà ^yAB=ˆB+ˆC (góc ngoài tại A của ΔABC)
^yBA=ˆA+ˆC (góc ngoài tại B của ΔABC)
Suy ra ˆG=1800−12(ˆA+ˆB+2ˆC)
=1800−12(1800+ˆC) vì ˆA+ˆB+ˆC=1800
=900−12ˆC=1800−ˆC2=ˆA+ˆB+ˆC−ˆC2
Vậy ˆG=ˆA+ˆB2
Tương tự: ˆF=ˆA+ˆC2
ˆE=ˆB+ˆC2
b) Kẻ GH, GK, GM lần lượt vuông góc với AC, AB, BC.
Ta có: GH=GK (vì G thuộc phân giác ^xAB )
GK = GM (vì G thuộc phân giác ^yBA)
Suy ra GH = GM, nên G nằm trên đường phân giác của ^ACB hay đường phân giác của góc C đi qua G.
Tương tự đường phân giác của góc B đi qua F, đường phân giác của góc A đi qua E.
Câu 2: Cho tam giác cân ABC (AB = AC). Các đường cao BH và CK cắt nhau tại I. Chứng minh AI là phân giác của góc BAC.
Hướng dẫn giải
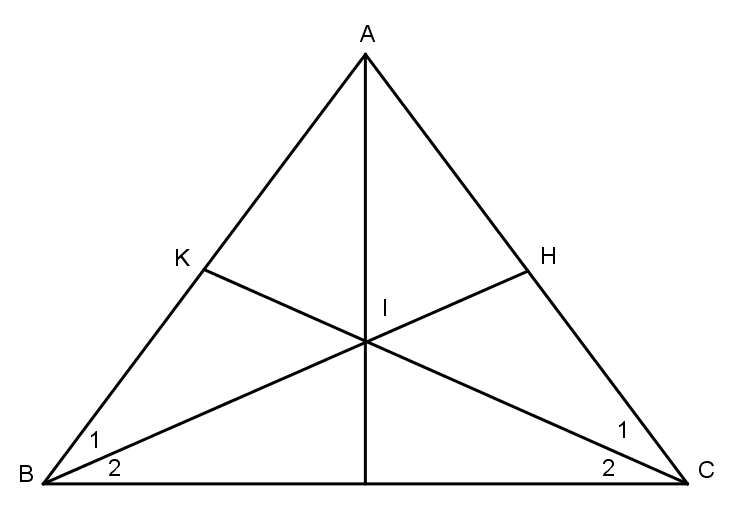
Ta có: ^C1=^B1 (cùng phụ ˆA) (1)
Suy ra: ^C2=^B2
Do đó ΔIBC cân tại tại I nên IB = IC (2)
Từ (1) và (2) ta có:
ΔIHC=ΔIKB (cạnh huyền, góc nhọn)
Nên IH=IK
Vậy AI là phân giác của góc BAC.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho góc vuông xOy và tam giác vuông cân ABC có ˆA=900, B thuộc Ox, C thuộc Oy, A và O thuộc hai nửa mặt phẳng đối nhau bờ BC. Chứng minh rằng OA là tia phân giác của góc xOy.
Câu 2: Chứng minh rằng trong một tam giác ba phân giác của hai góc ngoài và một góc trong không kề với chúng gặp nhau tại một điểm.
Câu 3: Cho góc vuông xOy và tam giác vuông cân ABC có ˆA=900, B thuộc Ox, C thuộc Oy, A và O thuộc hai nửa mặt phẳng đối nhau bờ BC. Chứng minh rằng OA là tia phân giác của góc xOy.
3.2. Bài tập trắc nghiệm
Câu 1: Điểm E nằm trên tia phân giác góc A của tam giác ABC ta có
A. E nằm trên tia phân giác góc B
B. E cách đều hai cạnh AB, AC
C. E nằm trên tia phân giác góc C
D. EB = EC
Câu 2: Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
A. AI là trung tuyến vẽ từ A
B. AI là đường cao kẻ từ A
C. AI là trung trực cạnh BC
D. AI là phân giác góc A
Câu 3: Em hãy chọn câu đúng nhất
A. Ba tia phân giác của tam giác cùng đi qua một điểm, điểm đó gọi là trọng tâm của tam giác
B. Giao điểm ba đường phân giác của tam giác cách đều ba cạnh của tam giác
C. Trong một tam giác, đường trung tuyến xuất phát từ một đỉnh đồng thời là đường phân giác ứng với cạnh đáy
D. Giao điểm ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Câu 4: Cho ΔABC có ∠A = 70°, các đường phân giác của BE và CD của ∠B và ∠C cắt nhau tại I. Tính ∠BIC ?
A. 125°
B. 100°
C. 105°
D. 140°
Câu 5: Cho ΔABC, các tia phân giác góc B và A cắt nhau tại điểm O. Qua O kẻ đường thẳng song song BC cắt AB tại M , cắt AC tại N. Cho BM = 2cm, CN = 3cm. Tính MN ?
A. 5cm
B. 6cm
C. 7cm
D. 8cm
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Hiểu được định nghĩa, tính chất của tia phân giác của một góc.
- Áp dụng để giải các bài toán liên quan.
Tham khảo thêm
- doc Toán 7 Chương 3 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Toán 7 Chương 3 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Toán 7 Chương 3 Bài 3: Quan hệ giữa ba cạnh của một tam giác Bất đẳng thức tam giác
- doc Toán 7 Chương 3 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Toán 7 Chương 3 Bài 6: Tính chất ba đường phân giác của tam giác
- doc Toán 7 Chương 3 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Toán 7 Chương 3 Bài 8: Tính chất ba đường trung trực của tam giác
- doc Toán 7 Chương 3 Bài 9: Tính chất ba đường cao của tam giác