Toán 7 Chương 1 Bài 1: Tập hợp Q các số hữu tỉ
Mời các em cùng tham khảo nội dung bài giảng Tập hợp Q các số hữu tỉ do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Số hữu tỉ là gì?
- Số hữu tỉ là số có thể viết dưới dạng \(\frac{a}{b}\) với a, b ∈ \( \mathbb{Z}\), b # 0.
- Tập hợp các số hữu tỷ được kí hiệu là \(\mathbb{Q}\).
Ví dụ: Xét các số 2; 0 và 0.5, ta thấy:
\(2 = \frac{2}{1} = \frac{4}{2} = \frac{8}{4} = ...\)
\(0 = \frac{0}{1} = \frac{0}{2} = \frac{0}{3} = ...\)
\( - 0,5 = - \frac{1}{2} = - \frac{2}{4} = - \frac{3}{6} = ...\)
Vậy các số 2, 0, -0.5 là các số hữu tỉ.
Nhận xét: \( \mathbb{N} \subset \mathbb{Z}\subset \mathbb{Q}\).
1.2. Biểu diễn số hữu tỉ trên trục số
Để biểu diễn số hữu tỉ \(\frac{a}{b}\) (a, b ∈ \( \mathbb{Z}\), b > 0) trên trục số ta làm như sau:
-
Chia đoạn đơn vi [0;1] trên trục số thành b phần bằng nhau, lấy 1 đoạn đoạn làm đơn vị mới thì đơn vị mới bằng \(\frac {1}{b}\) đơn vị cũ.
-
Nếu a>0 thì số \(\frac {a}{b}\) được biểu diễn bởi một điểm nằm bên phải điểm 0 một đoạn bằng \(\left |a \right |\) lần đơn vị mới.
-
Nếu a<0 thì số \(\frac {a}{b}\) được biểu diễn bởi một điểm nằm bên trái điểm 0 một đoạn bằng \(\left |a \right |\) lần đơn vị mới.
-
Trên trục số, điểm biểu diễn số hữu tỉ x được gọi là điểm x.
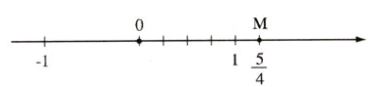
Ví dụ: Biết diễn số hữu tỉ \(\dfrac {5}{4}\) trên trục số:
1.3. So sánh số hữu tỉ
Để so sánh hai số hữu tỉ x,y ta làm như sau:
- Viết x,y dưới dạng phân số cùng mẫu dương.
- So sánh các tử là số nguyên a và b.
- Nếu a> b thì x > y.
- Nếu a = b thì x=y.
- Nếu a < b thì x < y.
1.4. Chú ý
-
Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
-
Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
-
Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
2. Bài tập minh họa
Câu 1: Với ba chữ số 1, hãy biểu diễn số hữu tỉ âm nhỏ nhất, số hữu tỉ âm lớn nhất.
Hướng dẫn giải
Số hữu tỉ âm nhỏ nhất -111.
Số hữu tỉ âm lớn nhất \( - \frac{1}{{11}}\).
Câu 2: So sánh các số hữu tỉ sau bằng cách nhanh nhất:
a. \(\frac{{ - 1}}{3}\) và \(\frac{1}{{100}}\)
b. \(\frac{{ - 231}}{{232}}\) và \(\frac{{-1321}}{{1320}}\)
c. \(\frac{{ - 13}}{{38}}\) và \(\frac{{29}}{{ - 88}}\)
d. \(\frac{{ - 27}}{{29}}\) và \(\frac{{ - 272727}}{{292929}}\)
Hướng dẫn giải
a. \(\frac{{ - 1}}{3} < 0 < \frac{1}{{100}} \Rightarrow \frac{{ - 1}}{3} < \frac{1}{{100}}\).
b. \(\frac{{231}}{{232}} < 1 < \frac{{1321}}{{1320}} \Rightarrow \frac{{ - 231}}{{232}} > \frac{{ - 1321}}{{1320}}\).
c. \(\frac{{13}}{{38}} > \frac{{13}}{{39}} = \frac{1}{3} = \frac{{29}}{{87}} > \frac{{29}}{{88}} \Rightarrow \frac{{ - 13}}{{38}} < \frac{{29}}{{ - 88}}\).
d. \(\frac{{ - 27}}{{29}} = \frac{{ - 27.10101}}{{29.10101}} = \frac{{ - 272727}}{{292929}}\) và \(\frac{{ - 272727}}{{292929}}\).
Câu 3: Cho hai số nguyên a và b trong đó a < b và b > 0. Chứng minh: \(\frac{a}{b} < \frac{{a + 1}}{{b + 1}}\).
Hương dẫn giải
Ta có:
\(\frac{a}{b} = \frac{{a(b + 1)}}{{b(b + 1)}} = \frac{{ab + a}}{{b(a + 1)}}\,\,\,\,\,\,\,\,\,b > 0,b + 1 > 0\).
\(\frac{{a + 1}}{{b + 1}} = \frac{{b(a + 1)}}{{b(b + 1)}} = \frac{{ab + b}}{{b(b + 1)}}\,\,\,\,\,\,\,\,\,b > 0\).
Mà a < b nên suy ra ab+ a < ab +b.
Vậy \(\frac{a}{b} < \frac{{a + 1}}{{b + 1}}\).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Với ba chữ số 3, hãy biểu diễn số hữu tỉ âm nhỏ nhất, số hữu tỉ âm lớn nhất.
Câu 2: So sánh các số hữu tỉ sau bằng cách nhanh nhất:
a. \(\frac{{ - 1}}{2}\) và \(\frac{1}{{99}}\)
b. \(\frac{{ - 197}}{{198}}\) và \(\frac{{-2345}}{{2344}}\)
3.2. Bài tập trắc nghiệm
Câu 1: Cách nào đúng trong các cách viết sau:
A. \( - 5 \in N\)
B. \( Q \in N\)
C. \( - \frac{3}{7} \in Z\)
D. \( - 5 \in Q\)
Câu 2: Số hữu tỉ x nhỏ hơn số hữu tỉ y nếu trên trực số:
A. điểm x ở bên phải điểm y
B. điểm x ở bên trái điểm y
C. điểm x và điểm y khác phía đối với điểm 0
D. cả 3 đáp án đều sai
Câu 3: Cách nào đúng trong các cách viết sau:
A. \(Q \subset Z\)
B. \(Z \subset N\)
C. \(Q \subset N\)
D. \(N \subset Q\)
Câu 4: Chọn câu sai trong các câu
A. Số \(2\dfrac{2}{9}\) là số hữu tỉ
B. Mọi số nguyên đều là số hữu tỉ
C. Số \(5\dfrac{1.09}{2.03}\) là số hữu tỉ
D. Số hữu tỉ là các số được viết dưới dạng [\frac{a}{b}] với a,b ϵ Ζ
Câu 5: Chọn câu đúng
A. Tập hợp các phân số bằng [-\frac{10}{29}] là [-\frac{10k}{29k}]
B. Số là số hữu tỉ \(\frac{0}{-19} âm
C. Tập hợp số tự nhiên là con của tập hợp số hữu tỉ
D. Nếu a và b cùng nhỏ hơn 0 thì phân số \(\frac{a}{b}<0\)
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
-
Định nghĩa số hữu tỉ.
-
Biểu diến số hữu tỉ trên trục số.
-
So sánh số hữu tỉ.
Tham khảo thêm
- doc Toán 7 Chương 1 Bài 2: Cộng, trừ số hữu tỉ
- doc Toán 7 Chương 1 Bài 3: Nhân, chia số hữu tỉ
- doc Toán 7 Chương 1 Bài 4: Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- doc Toán 7 Chương 1 Bài 5: Lũy thừa của một số hữu tỉ
- doc Toán 7 Chương 1 Bài 6: Lũy thừa của một số hữu tỉ (tiếp)
- doc Toán 7 Chương 1 Bài 7: Tỉ lệ thức
- doc Toán 7 Chương 1 Bài 8: Tính chất của dãy tỉ số bằng nhau
- doc Toán 7 Chương 1 Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- doc Toán 7 Chương 1 Bài 10: Làm tròn số
- doc Toán 7 Chương 1 Bài 11: Số vô tỉ. Khái niệm về căn bậc hai
- doc Toán 7 Chương 1 Bài 12: Số thực