Toán 9 Chương 4 Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ

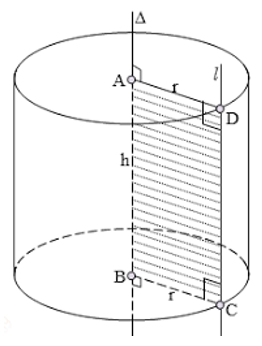
Khi quay hình chữ nhật $ABCD$ một vòng quanh cạnh $CD$ cố định ta thu được một hình trụ.

- Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.

- $DC$ là trục của hình trụ.

- Các đường sinh của hình trụ ( chẳng hạn $EF$) vuông góc với hai mặt đáy.

Độ dài đường sinh cũng là độ dài đường cao của hình trụ.

Với bán kính đáy r và chiều cao h, ta có:

Diện tích xung quanh: $S_{xq}=2\pi rh$

Diện tích toàn phần: $S_{tp}=2\pi rh+2\pi r^2$

Thể tích hình trụ được cho bởi công thức: $V=Sh=\pi r^2h$

Câu 1: Lọ gốm ở hình 74 có dạng một hình trụ. Quan sát hình và cho biết đâu là đáy, đâu là mặt xung quanh, đâu là đường sinh của hình trụ đó ?

Hướng dẫn giải

Đáy gồm 2 hình tròn ở trên và dưới của lọ gốm

Mặt xung quanh là mặt bên ngoài của lọ gốm

Đường sinh là đường thẳng nằm ở mặt xung quanh, nối 2 đáy của lọ gốm và vuông góc với đáy.

Câu 2: Tính thể tích hình trụ có chu vi hình tròn đáy là $100\pi(cm)$ và chiều cao là $3(m)$

Hướng dẫn giải

Ta có: Chu vi đáy $C=2\pi R=100\pi (cm)=0,1\pi (m)\Rightarrow R=0,05m$

Vậy, thể tích của hình trụ là $V=\pi R^2h=\pi .0,05^2.3=3 \pi 2,5.10^{-3}=7,5 \pi .10^{-3}(m^3)$

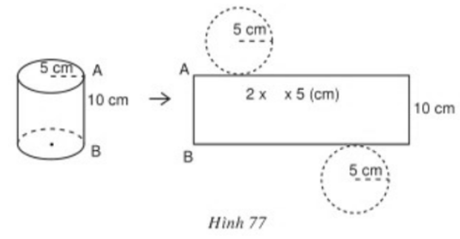
Câu 1: Quan sát hình 77 và điền số thích hợp vào các chỗ trống:

- Chiều dài của hình chữ nhật bằng chu vi của đáy hình trụ và bằng: (....)(cm).

- Diện tích hình chữ nhật

(....) . (....) = (....) (cm2).

- Diện tích một đáy của hình trụ

(....) . 5 . 5 = (....) (cm2).

- Tổng diện tích hình chữ nhật và diện tích hai hình tròn đáy (diện tích toàn phần) của hình trụ

(....) + (....) . 2 = (....) (cm2).

Hướng dẫn giải

- Chiều dài của hình chữ nhật bằng chu vi của đáy hình trụ và bằng: $10\pi$ (cm).

- Diện tích hình chữ nhật : $10.10\pi  = 100\pi \,\,\left( {c{m^2}} \right)$

- Diện tích một đáy của hình trụ: $\pi .5.5 = 25\pi \,\,\left( {c{m^2}} \right)$

- Tổng diện tích hình chữ nhật và diện tích hai hình tròn đáy (diện tích toàn phần) của hình trụ:

$100\pi  + 25\pi .2 = 150\pi \,\,\left( {c{m^2}} \right)$

Câu 2: Hình chữ nhật ABCD có $AB=a,BC=3a$. Quay hình chữ nhật quanh cạnh AB thì được thể tích $V_1$, quay quanh cạnh BC thì được thể tích là $V_2$. Tỉ số thể tích giữa  $V_1$ và $V_2$ là:

Hướng dẫn giải

Thể tích của hình trụ sinh ra khi quay quanh cạnh AB là: $V_1=\pi {R_{1}}^{2}h=\pi (3a)^2.a=9a^2 \pi$

Thể tích của hình trụ sinh ra khi quay quanh cạnh BC là: $V_2=\pi {R_{2}}^{2}h=\pi (a)^2.3a=3a^2 \pi$

Vậy tỉ số thể tích là $\frac{V_1}{V_2}=3$

Câu 1: Diện tích và chu vi của một hình chữ nhật $ABCD \;(AB > AD)$ theo thứ tự là $2a^2$ và $6a.$ Cho hình chữ nhật quay quanh cạnh $AB$ một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này.

Câu 2: Một hình trụ có bán kính đường tròn đáy là $6cm$, chiều cao $9cm$. Hãy tính:

a) Diện tích xung quanh của hình trụ.

b) Thể tích của hình trụ.

(Lấy $\pi  \approx 3,142$ làm tròn kết quả đến hàng đơn vị).

Câu 3: Diện tích xung quanh của một hình trụ là $10m^2$ và diện tích toàn phần của nó là $14m^2$. Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy $\pi  \approx 3,14,$ làm tròn kết quả đến chữ số thập phân thứ hai).

Câu 4: Một cái cốc hình trụ được đổ đầy sữa. Liệu em có thể rót ra đúng một nửa lượng sữa mà không cần phải sử dụng các công dụng cụ hay không?

Câu 1: Một hình trụ có đường cao bằng đường kính đáy. Thể tích của hình trụ là $128 \pi (cm^3)$. Diện tích xung quanh hình trụ là:

A. $16 \pi (cm^2)$

B. $32 \pi (cm^2)$

C. $64 \pi (cm^2)$

D. $128 \pi (cm^2)$

Câu 2: Hình trụ có chu vi đường tròn là $18\pi cm$, chiều cao là $5cm$. Thể tích hình trụ là:

A. $54 \pi (cm^3)$

B. $45 \pi (cm^3)$

C. $504 \pi (cm^3)$

D. $405 \pi (cm^3)$

Câu 3: Một hình trụ có bán kính đáy bằng $\frac{1}{3}$ đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là hình chữ nhật có diện tích là $60cm^2$. Diện tích xung quanh của hình trụ là:

A. $60\pi (cm^2)$

B. $70\pi (cm^2)$

C. $80\pi (cm^2)$

D. $90\pi (cm^2)$

Câu 4: Một hình có diện tích xung quanh là $20 \pi (cm^2)$ và diện tích toàn phần là $28 \pi (cm^2)$. Thể tích hình trụ đó là:

A. $5 \pi (cm^3)$

B. $10 \pi (cm^3)$

C. $15 \pi (cm^3)$

D. $20 \pi (cm^3)$

Câu 5: Tính thể tích của một hình trụ có chu vi đáy là $100 \pi (cm)$ và có đường cao bằng đường kính.

A. $0,25 \pi (m^3)$

B. $2,5 \pi (m^3)$

C. $25 \pi (m^3)$

D. $250 \pi (m^3)$

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Biết được các khái niệm về hình trụ ( đáy, trục, mặt xung quanh, đường sinh  độ dài đường cao, mặt cắt . .. của hình trụ ) .
• Sử dụng được công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình trụ.
• Thấy được ứng dụng thực tế của hình trụ