Toán 9 Chương 1 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Một số hệ thức về cạnh và góc trong tam giác vuông. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Các hệ thức
.jpg)
Định lý: Trong tam giác vuông mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề.
b) Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cotan góc kề.
Cụ thể trong tam giác trên thì:
\(b=a.sinB=a.cosC;c=a.sinC=a.cosB\)
\(b=c.tanB=c.cotC;c=b.tanC=b.cotB\)
1.2. Áp dụng giải tam giác vuông
Cho tam giác ABC vuông tại A có BC=10 và \(\widehat{C}=30^{\circ}\). Giải tam giác vuông ABC.
Hướng dẫn giải
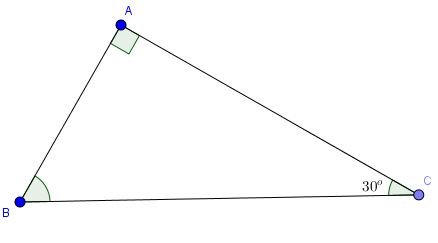
Ta dễ dàng suy ra: \(\widehat{B}=60^{\circ}\)
\(AC=BC.cosC=10.cos30^{\circ}=10.\frac{\sqrt{3}}{2}=5.\sqrt{3}\)
\(AB=BC.sinC=10.sin30^{\circ}=10.\frac{1}{2}=5\)
2. Bài tập minh họa
Câu 1. Cho tam giác ABC vuông tại A, có BC=14. Tính độ dài AB, AC biết AB=AC
Hướng dẫn giải
Vì AB=AC nên tam giác ABC vuông cân tại A suy ra: \(\widehat{B}=\widehat{C}=45^{\circ}\)
Khi đó: \(AB=AC=BC.sin45^{\circ}=14.\frac{1}{\sqrt{2}}=7\sqrt{2}\)
Câu 2. Một cái cây cao 10m tại một thời điểm bóng của cây trên mặt đất là 4m. Hãy tính góc (làm tròn tới phút) mà tia sáng mặt trời tạo với mặt đất.
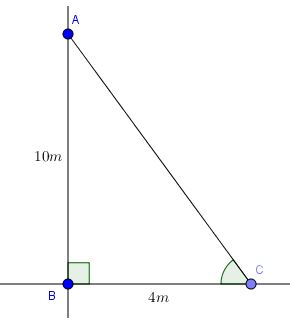
Hướng dẫn giải:
Ta xem cái cây, hướng tia sáng và mặt đất hợp thành tam giác ABC như hình vẽ
Khi đó: \(\widehat{ACB}\) chính là góc mà tia sáng mặt trời tạo với mặt đất
Ta có: \(tan\widehat{ACB}=\frac{AB}{BC}=\frac{10}{4}=\frac{5}{2}\Rightarrow \widehat{ACB}\approx 60^{\circ}12{}'\)
Câu 3. Một con thuyền băng qua một khúc sông với vận tốc là 3km/h trong vòng 6 phút. Biết rằng hướng thuyền đi tạo với bờ 1 góc 60 độ. Tính chiều rộng (m) của khúc sông đó
Hướng dẫn giải:
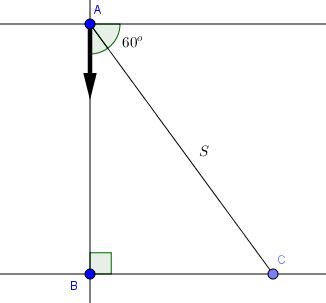
Ta sẽ xem mô tả đề bài như trong hình vẽ ta sẽ giải bài toán thông qua giải tam giác ABC như hình
dễ dàng thấy được \(\widehat{BAC}=30^{\circ}\) ta sẽ đổi đơn vị: \(3km/h=\frac{5}{6}m/s\), 6 phút=360 (s)
\(\Rightarrow S=\frac{5}{6}.360=300(m)\)\(\Rightarrow AB=S.cos30^{\circ}=300.\frac{\sqrt{3}}{2}=150\sqrt{3}(m)\)
Câu 4. Chứng minh rằng diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy
Hướng dẫn giải
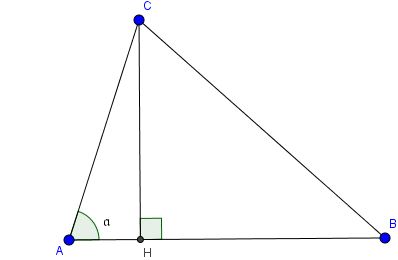
Với tam giác ABC đặt góc tạo bởi AB và AC là \(\alpha\). ta sẽ Cm: \(S_{\Delta ABC}=\frac{1}{2}.AB.AC.sin\alpha\)
Ta có: \(\Delta AHC\) vuông tại H nên: \(CH=AC.sin\alpha\)
\(S_{\Delta ABC}=\frac{1}{2}.AB.CH=\frac{1}{2}.AB.AC.sin\alpha\)
Câu 5. Cho tam giác ABC nhọn có BC=a, AB=c, AC=b. Chứng minh rằng: \(a^2=b^2+c^2-2.b.c.cosA\)
Hướng dẫn giải
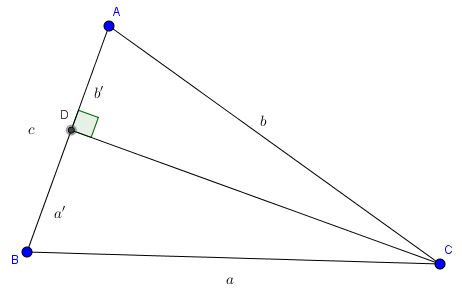
Vẽ CD vuông góc với AB (D thuộc AB)
Đặt \(AD=b',BD=a'\Rightarrow c=a'+b'\)
Áp dụng định lý Py-ta-go ta có: \(a^2=a'^2+CD^2=(c-b')^2+b^2-b'^2=c^2+b^2-2.c.b'\)
mà \(b'=b.cosA\Rightarrow a^2=b^2+c^2-2.b.c.cosA\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1. Cho tam giác ABC vuông tại A, có BC= 20cm. Tính độ dài AB, AC biết AB=AC.
Câu 2. Một cái cây cao 8m tại một thời điểm bóng của cây trên mặt đất là 6m. Hãy tính góc (làm tròn tới phút) mà tia sáng mặt trời tạo với mặt đất.
Câu 3. Một con cano băng qua một khúc sông với vận tốc là 20 km/h trong vòng 2 phút. Biết rằng hướng thuyền đi tạo với bờ 1 góc 30 độ. Tính chiều rộng (m) của khúc sông đó?
Câu 4. Cho tam giác ABC nhọn có BC=a, AB=c, AC=b. Chứng minh rằng: \({{c}^{2}}={{a}^{2}}+{{b}^{2}}-2.a.b.\cos C\)
3.2. Bài tập trắc nghiệm
Câu 1. Cho tam giác ABC vuông tại A có BC=8, \(\widehat{C}=30^{\circ}\). \(S_{\Delta ABC}\) có giá trị là:
A. \(8\sqrt{2}\) B. \(8\sqrt{3}\)
C. \(4\sqrt{3}\) D. \(4\sqrt{2}\)
Câu 2. Cho tam giác ABC vuông tại A có AB-AC=6. Biết rằng \(\widehat{C}=\alpha, tan\alpha =3\). Giá trị của \(S_{\Delta ABC}\) là:
A. 13 B. 14,5
C. 13,5 D. 14
Câu 3. Cho tứ giác ABCD có AC=8, BD=10, \(\widehat{AOB}=30^{\circ}\). Giá trị của \(S_{ABCD}\) là:
A. 20 B. 22
C. 12 D. 18
Câu 4. Cho 2 tam giác vuông ABC (tại A) và A'B'C' (tại A') lần lượt có: \(\widehat{C}=30^{\circ}\),BC=6, \(\widehat{C'}=45^{\circ}\), B'C'=4. So sánh AB và A'B'
A. \(AB>A'B'\)
B. \(A'B'>AB\)
C. \(AB=A'B'\)
D. Không thể so sánh được
Câu 5. Cho tam giác ABC vuông tại A có BC=6. \(\widehat{B}=60^{\circ}\). đường cao AH. Gọi E, F lần lượt là hình chiếu vuông góc của H lên AB, AC
Giá trị của biểu thức S=AE.AB+AF.FC là bao nhiêu
A. \(\frac{27}{4}\)
B. \(\frac{27}{2}\)
C. \(\frac{27\sqrt{3}}{2}\)
D. \(\frac{27}{\sqrt{2}}\)
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Nắm vững các hệ thức về cạnh và góc trong tam giác vuông.
- Vận dụng kiến thức để làm bài toán về giải tam giác vuông.
Tham khảo thêm
- docx Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
- docx Toán 9 Chương 1 Bài 2: Tỉ số lượng giác của góc nhọn
- docx Toán 9 Chương 1 Bài 3: Bảng lượng giác
- docx Toán 9 Chương 1 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
