Toán 9 Chương 1 Bài 2: Tỉ số lượng giác của góc nhọn
eLib xin giới thiệu đến các em học sinh lớp 9 nội dung bài Tỉ số lượng giác của góc nhọn. Bài giảng được biên soạn đầy đủ và chi tiết, đồng thời được trình bày một cách logic, khoa học sẽ giúp các em ôn tập và củng cố kiến thức về Tỉ số lượng giác của góc nhọn.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khái niệm tỉ số lượng giác của một góc nhọn
Nhận xét: Từ định nghĩa trên, dễ thấy các tỉ số lượng giác của một góc nhọn luôn luôn dương. Hơn nữa ta có: \(\sin\alpha < 1, \cos\alpha <1\)
Chú ý: Nếu hai góc nhọn \(\alpha\) và \(\beta\) có \(\sin\alpha =\sin\beta\) ( hoặc \(\cos\alpha =\cos\beta , \tan\alpha =\tan\beta ,\cot \alpha =\cot \beta\) ) thì \(\alpha =\beta\) vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.
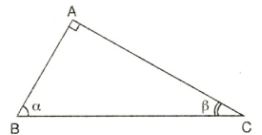
1.2. Tỉ số lượng giác của hai góc phụ nhau
Định lý: Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.
Cụ thể trong hình trên với \(\alpha\) và \(\beta\) là hai góc phụ nhau nên: \(\sin\alpha =\cos\beta , \cos\alpha =\sin\beta, \tan \alpha =\cot\beta , \cot\alpha =\tan\beta\)
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu "^". Chẳng hạn viết \(\sin A\) thay vì viết \(\sin\widehat{A}\)
Từ định nghĩa các tỉ số lượng giác của một góc nhọn ta có: \(\tan\alpha =\frac{\sin\alpha }{\cos\alpha }; \cot\alpha =\frac{\cos\alpha }{\sin\alpha }\)
và \(\tan\alpha .\cot\alpha =1 , \sin^2\alpha +\cos^2\alpha =1\); \(1+\tan^2\alpha =\frac{1}{\cos^2\alpha }; 1+cot^2\alpha =\frac{1}{sin^2\alpha }\)
(các công thức trên có thể chứng minh dễ dàng)
2. Bài tập minh họa
2.1. Dạng 1: Tính tỉ số lượng giác bằng khái niệm
Câu 1. Cho tam giác ABC vuông tại A, có AB=6, BC=10. Tính sinB và cosB
Hướng dẫn giải
Ta có: \(\cos B=\frac{AB}{BC}=\frac{6}{10}=0.6 ;AC=\sqrt{BC^2-AB^2}=8 \Rightarrow \sin B=\frac{AC}{BC}=0.8\)
2.2. Dạng 2: Tính tỉ số lượng giác bằng công thức liên hệ giữa hai góc phụ nhau
Câu 1. Chuyển các tỉ số lượng giác sau thành các tỉ số lượng giác của các góc nhỏ hơn \(45^{\circ}\) : \(\sin72^{\circ};\cos50^{\circ}; \tan68^{\circ}; \cot 88^{\circ}\)
Hướng dẫn giải
Ta có: \(\sin72^{\circ}=cos18^{\circ};\cos50^{\circ}=\sin40^{\circ}; \tan68^{\circ}=\cot22^{\circ}; \cot88^{\circ}=\tan2^{\circ}\)
Câu 2. Cho tam giác ABC. Biết cosB=0,6. Tính các tỉ số lượng giác góc C.
Hướng dẫn giải
Ta có: \(\sin C=\cos B=0.6\) và \(\cos C=sin B=\sqrt{1-\cos^2B}=0.8\)
\(\tan C=\frac{\sin C}{\cos C}=\frac{0.6}{0.8}=\frac{3}{4}\) và \(\cot C=\frac{\cos C}{\sin C}=\frac{0.8}{0.6}=\frac{4}{3}\)
Câu 3.
a) Rút gọn biểu thức: \(S=\cos^2\alpha +\tan^2\alpha .\cos^2\alpha\)
b) chứng minh: \(\frac{(\sin\alpha +\cos\alpha )^2-(\sin\alpha -\cos\alpha )^2}{\sin\alpha .\cos\alpha }=4\)
Hướng dẫn giải
a) \(S=\cos^2\alpha +\tan^2\alpha .\cos^2\alpha\)
\(=\cos^2\alpha+\frac{\sin^2\alpha }{\cos^2\alpha }.\cos^2\alpha \)
\(=\sin^2\alpha +\cos^2\alpha =1\)
b) \(VT=\frac{(1+2.\sin\alpha .\cos\alpha )-(1-2.\sin\alpha .\cos\alpha )}{\sin\alpha.\cos\alpha }=\frac{4.\sin\alpha .\cos\alpha }{\sin\alpha .\cos\alpha }=4\)
( Áp dụng: \(\sin^2\alpha +\cos^2\alpha =1\) )
Câu 4. Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh: \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
Hướng dẫn giải
Kẻ AH vuông góc với BC ( \(H\in BC\) )
Khi đó: \(\sin B=\frac{AH}{c}\Rightarrow \sin B.c=AH\) và \(\sin C=\frac{AH}{b}\Rightarrow \sin C.b=AH\)
từ đó ta có: \(\sin B.c=\sin C.b\Rightarrow \frac{b}{\sin B}=\frac{c}{\sin C}\) .
Tương tự kẻ đường cao BD ( \(D\in AC\) ) sẽ chứng minh được: \(\frac{a}{\sin A}=\frac{b}{\sin B} \Rightarrow \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1. Cho tam giác ABC vuông tại A, có AC=3, BC=5. Tính sinC và cosC.
Câu 2. Chuyển các tỉ số lượng giác sau thành các tỉ số lượng giác của các góc nhỏ hơn \({{45}^{{}^\circ }}\) : \(\sin {{83}^{{}^\circ }};\,\,\,\cos {{49}^{{}^\circ }};\,\,\,\tan {{79}^{{}^\circ }};\,\,\cot {{98}^{{}^\circ }}\)
Câu 3. Cho tam giác ABC vuông tại A. Biết sinC=0,6. Tính các tỉ số lượng giác góc B.
Câu 4. Chứng minh các đẳng thức sau:
a) \({{\cos }^{4}}x-{{\sin }^{4}}x={{\cos }^{2}}x-{{\sin }^{2}}x\)
b) \({{\sin }^{4}}x+{{\cos }^{2}}x.{{\sin }^{2}}x+{{\sin }^{2}}x=2{{\sin }^{2}}x\)
c) \(\left( 1+\tan x \right)\left( 1+\cot x \right)-2=\frac{1}{\sin .\cos x}\)
Câu 5. Cho tam giác ABC vuông tại A, BC = a, CA = b, AB = c. Chứng minh rằng: \(\tan \frac{B}{2}=\frac{b}{c+a}.\)
3.2. Bài tập trắc nghiệm
Câu 1. Tam giác OPQ có OP =7,2, OQ = 9,6, PQ =12. Tìm số đo các góc của tam giác
A. góc O = 60, P = 50, Q = 70
B. góc O = 70, P = 50, Q = 60
C. góc O = 90, P = 53, Q = 37
D. Một kết quả khác
Câu 2. Tam giác ABC có B=60 độ, C =45 độ và AB = 10. Chu vi tam giác ABC là
A. 35,9
B. 38,1
C. 42,5
D. 48,3
Câu 3. Tam giác ABC vuông tại A có cosB = 0,8. Vậy cotC là:
A. \(5 \over 3\)
B. \(3 \over 4\)
C. \(3 \over 5\)
D. \(3 \over 4\)
Câu 4. Cho tam giác ABC vuông tại C. Biết \(\cos A=\frac{5}{13}\). Khi đó tan B=?
A. \(\frac{12}{13}\)
B. \(\frac{5}{12}\)
C. \(\frac{12}{5}\)
D. \(\frac{13}{12}\)
Câu 5. Cho góc nhọn \(\alpha\) biết rằng: \(\cos\alpha -\sin\alpha =\frac{1}{5}\) Giá trị của \(\tan\alpha\) là:
A. 1
B. \(\frac{1}{2}\)
C. \(\frac{4}{5}\)
D. \(\frac{3}{4}\)
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Khái niệm tỉ số lượng giác của một góc nhọn.
- Tỉ số lượng giác của hai góc phụ nhau.
Tham khảo thêm
- docx Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
- docx Toán 9 Chương 1 Bài 3: Bảng lượng giác
- docx Toán 9 Chương 1 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
- docx Toán 9 Chương 1 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời