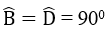Toán 9 Chương 2 Bài 2: Đường kính và dây của đường tròn

Định lý 1: Trong các dây của một đường tròn, dây lớn nhất là đường kính

Định lý 2

- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.

- Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

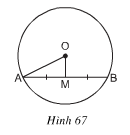
Câu 1: Cho hình 67. Hãy tính độ dài dây AB, biết OA = 13 cm, AM = MB, OM = 5 cm.

Hướng dẫn giải

Xét (O) có OM là 1 phần đường kính đi qua trung điểm M của dây AB 

\( \Rightarrow OM \bot AB\) (định lý)

Xét tam giác OAM vuông tại M có:

\(\eqalign{&  O{A^2} = A{M^2} + O{M^2}  \cr &  \Rightarrow AM = \sqrt {O{A^2} - O{M^2}}  = \sqrt {{{13}^2} - {5^2}}  = 12  \cr &  \Rightarrow AB = 2AM = 24\,\,\left( {cm} \right) \cr} \)

Câu 2: Cho đường tròn tâm O đường kính AB, dây CD không cắt AB. Gọi H, K lần lượt là hình chiếu vuông góc của A,B lên CD. CM: CH=DK

Hướng dẫn giải

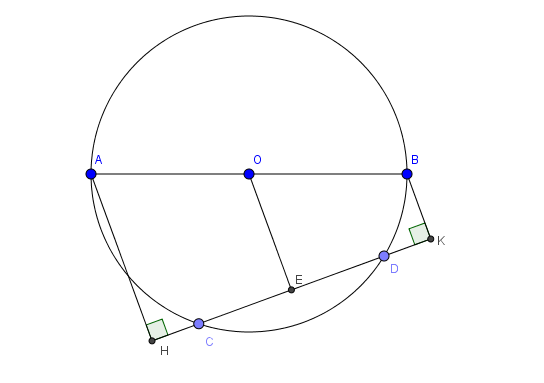
Dựng OE vuông góc với CD (E thuộc CD) theo định lý 2 thì E là trung điểm CD.                             (1)

Xét hình thang ABKH có O là trung điểm AB và  \(OE\parallel AH\parallel BK\) nên E là trung điểm HK.     (2)

Từ (1) và (2) thì ta có CH=DK

Câu 1: Cho (O;R) đường kính AB, H là trung điểm OB. Vẽ dây CD vuông góc với AB tai H, K là trung điểm của AC và I là trung điểm đối xứng của A qua H

a) CMR: 4 điểm C, H, O, K cùng thuộc một đường tròn

b) CM ADIC là hình thoi. Tính diện tích theo R

Hướng dẫn giải

a) Kẻ OK, vì K là trung điểm AC nên OK vuông góc AC khi đó 4 điểm K, O, H, C sẽ cùng thuộc đường tròn đường kính OC

b) Xét tứ giác ADIC có 2 đường chéo cắt nhau tại trung điểm mỗi đường nên ADIC là hình bình hành.

Xét tam giác ADC có AH là đường cao vừa là trung tuyến ( OH vuông góc với CD thì đi qua trung điểm CD) nên Tam giác ACD cân tại A nên AC=AD

Khi đó ADIC là hình thoi.

\(S_{ADIC}=S_{\Delta ADC}+S_{\Delta DIC}=2.S_{\Delta ADC}=AH.CD\)

Mà \(AH=\frac{3R}{2}\) ; \(CD=2.CH=2.\sqrt{OC^2-OH^2}=2\sqrt{R^2-\frac{R^2}{4}}=R\sqrt{3}\)

\(\Rightarrow S_{ADIC}=\frac{3R}{2}.R\sqrt{3}=\frac{3R^2\sqrt{3}}{2}\)

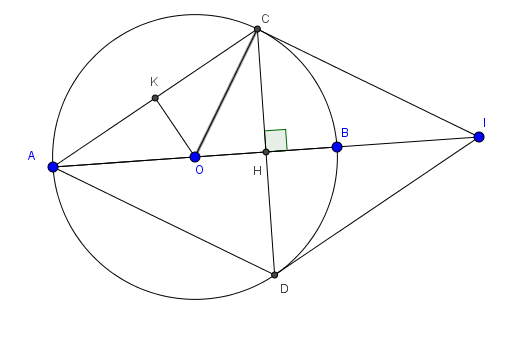
Câu 2: Cho tam giác ABC nhọn (AB

a) Chứng minh tứ giác BHCD là hình bình hanh

b) Chứng minh \(OM=\frac{1}{2}.AH\)

Hướng dẫn giải

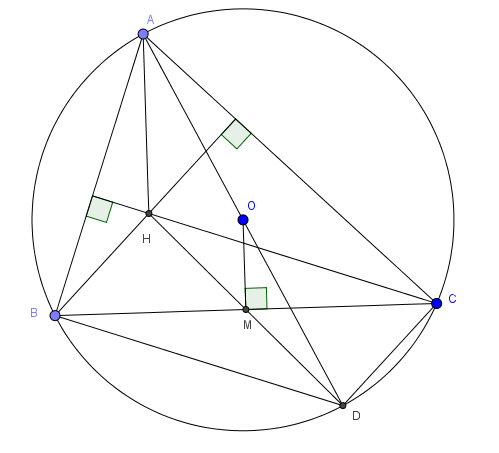
a) Tam giác ABD có OA=OB=OD với O là trung điểm AD nên ABD vuông tại B \(\Rightarrow BD\perp AB\Rightarrow BD\parallel CH\) 

tương tự cho tam giác ADC vuông tại C \(\Rightarrow CD\perp AC\Rightarrow BH\parallel CD\)

Tứ giác BHCD có các cặp cạnh đối song song nên BHCD là hình bình hành

b) ta có OM vuông góc BC nên M là trung điểm BC. Mà BHCD là hình bình hành nên đường chéo HD đi qua trung điểm BC là M

Xét tam giác AHD có O là trung điểm AD, M là trung điểm HD nên OM là đường trung bình tam giác AHD \(\Rightarrow OM=\frac{1}{2}.AH\)

Câu 1: Cho tam giác ABC, các đường cao BH và CK. Chứng minh:

a. Bốn điểm B, C, H, K cùng thuộc một đường tròn

b. HK < BC

Câu 2: Tứ giác ABCD có 

a. Chứng minh rằng bốn điêm A, B, C, D cùng thuộc một đường tròn

b. So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?

Câu 3: Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đên EF. Chứng minh rằng IE = KF.

Câu 4: Cho đường tròn (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Câu 1: Cho đường tròn (O;R) đường kính AB. M là một điểm nằm giữa A và B. Qua M vẽ dây CD vuông góc với AB. Biết AM=4, R=6,5. Giá trị diện tích tam giác BCD là bao nhiêu? 

A. 50

B. 52

C. 54

D. 56

Câu 2: Cho đường tròn (O;R) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O) tại H. Biết CD=16, MH=4. R=?

A. 8

B. 9

C. 10

D. 11

Câu 3: Cho đường tròn (O;R) và 2 dây AB và CD bằng nhau và vuông góc với nhau tại I. Giả sử IA=2, IB=4. Khoảng cách từ tâm O tới AB là d và tới CD là d'

Giá trị của d và d'

A. \(d=2;d'=1\)

B. \(d=d'=1\)

C. \(d=d'=2\)

D. \(d=1;d'=2\)

Câu 4: Cho đường tròn (O;12) có đường kính CD. Dẫy MN qua trung điểm I của OC sao cho góc NID bằng 30 độ. MN=?

A. \(3\sqrt{3}\)

B. \(2\sqrt{3}\)

C. \(3\)

D. \(2\)

Câu 5: Cho (O;25), dây AB=40. Vẽ dây CD song song với AB và có khoảng cách tới AB là 22. Độ dài dây CD là?

A. 42

B. 44

C. 46

D. 48

Qua bài học này, các em nắm được một số nọi dung chính như sau:

• Nắm được đường kính là dây lớn nhất trong các dây của đườngtròn, nắm được hai định lý về đường kính vuông góc với dây và đường kính đi quatrung điểm của dây không đi qua tâm.
• Biết vận dụng các định lý để chứngminh đường kính đi qua trung điểm của một dây, đường kính vuông góc với dây.