Toan 9 Ôn tập chương 2: Hàm số bậc nhất

Hàm số bậc nhất là hàm số được viết dưới dạng \(y=ax+b(a\neq 0)\)

Hàm số đồng biến trên \(\mathbb{R}\) khi a dương.

Hàm số nghịch biến trên \(\mathbb{R}\) khi a âm.

Đồ thị hàm số bậc nhất là một đường thẳng:

Cắt trục tung tại điểm có tung độ bằng b

Song song với đường thẳng \(y=ax\), và cũng chính là đường thẳng \(y=ax\) nếu \(b=0\)

Chúng ta có 3 vị trí của hai đường thẳng \(y=ax+b;y=a'x+b'(a;a'\neq 0)\)

Song song: \(\left\{\begin{matrix} a=a'\\ b\neq b' \end{matrix}\right.\)

Trùng nhau: \(\left\{\begin{matrix} a=a'\\ b= b' \end{matrix}\right.\)

Cắt nhau: \(a\neq a'\)

Lưu ý: Đối với vị trí cắt nhau, ta cũng có trường hợp đó là hai đường thẳng vuông góc với nhau

khi đó: \(a.a'=-1\)

Về phương trình đường thẳng dạng chuẩn đó là \(y=ax+b(a\neq 0)\), ta có hệ số góc của phương trình này chính là \(a\)

Đôi khi, phương trình đường thẳng được viết dưới dạng \(ax+by+c=0\)

Thì ta sẽ biến đổi một chút thành dạng chuẩn:

\(ax+by+c=0(b\neq 0)\)\(\Leftrightarrow by=-ax-c\)\(\Leftrightarrow y=-\frac{a}{b}x-\frac{c}{b}\); hệ số góc của phương trình này chính là \(\frac{-a}{b}\).

Cho hàm số \(y=ax-2\). Xác định hệ số góc của hàm số đó, biết rằng hàm số đi qua điểm \(A(2;4)\). Vẽ đồ thị hàm số đó trên trục tọa độ.

Hướng dẫn giải

Do hàm số đi qua điểm \(A(2;4)\) nên tọa độ của điểm A cũng thuộc đồ thị hàm số.

Thế hoành độ và tung độ của điểm A vào hàm số, ta được:

\(4=a.2-2\)\(\Leftrightarrow a=3\)

Vậy, hàm số được cho có dạng: \(y=3x-2\) với hệ số góc \(a=3\)

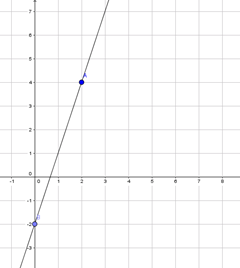
Vẽ đồ thị:

Hàm số qua các điểm: \(A(2;4)\); \(B(0;-2)\)

a) Với giá trị nào của m thì hàm số \(y=(m-2)x-6\) đồng biến trên \(\mathbb{R}\)?

b) Với các giá trị nào của n thì hàm số \(y=(4-n)x+2017\) nghịch biến trên \(\mathbb{R}\)?

Hướng dẫn giải

a) Để hàm số \(y=(m-2)x-6\) đồng biến trên \(\mathbb{R}\) thì hệ số góc \(a>0\)

Tức là \(m-2>0\Leftrightarrow m>2\)

Vậy \(m>2\) thì hàm số đồng biến trên \(\mathbb{R}\)

b) Để hàm số \(y=(4-n)x+2017\) nghịch biến trên \(\mathbb{R}\) thì hệ số góc \(a<0\)

Tức là \(4-n<0\Leftrightarrow n>4\)

Vậy \(n>4\) thì hàm số nghịch biến trên \(\mathbb{R}\)

Xác định các hệ số a, b để hai hàm số sau: \(y=ax+(b+3)\) và \(y=(4-a)x+(b+10)\)

a) Vuông góc

b) Song song

c) Trùng nhau

Hướng dẫn giải

Để các hàm số trên là hàm số bậc nhất, trước hết hệ số góc khác 0

\(\Leftrightarrow \left\{\begin{matrix} a\neq 0\\ a\neq 4 \end{matrix}\right.\)

a) Để hai hàm số vuông góc với nhau, ta có:

\(a(4-a)=-1\Leftrightarrow a^2-4a-1=0\)

\(\Leftrightarrow a=2+\sqrt{5}\) hoặc \(a=2-\sqrt{5}\) thì hai đường thẳng vuông góc với nhau.

b) Để hai hàm số song song với nhau, ta có:

\(\left\{\begin{matrix} a=4-a\\ b+3\neq b+10 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} a=2\\ 0.b\neq 7 \end{matrix}\right.\)

Vậy \(a=2\) thì hai đường thẳng song song với nhau.

c) Để hai hàm số trùng nhau, ta có

\(\left\{\begin{matrix} a=4-a\\ b+3=b+10 \end{matrix}\right.\)

Không thể làm cho \(b+3=b+10\) nên hai đường thẳng này không thể trùng nhau với mọi hệ số a, b.

Vẽ các đồ thị sau trên cùng một mặt phẳng tọa độ

\(y=x+2\)

\(y=2x-1\)

\(y=3-x\)

Chứng tỏ rằng tam giác tạo bởi 3 điểm là 3 tọa độ giao nhau của 3 đường thẳng trên là một tam giác vuông.

Hãy dùng đồ thị kiểm chứng lại.

Hướng dẫn giải

Gọi đồ thị \(y=x+2\) là \(d_1\), \(y=2x-1\) là \(d_2\), \(y=3-x\) là \(d_3\)

Hàm số \(d_1\) qua \(A(0;2);B(1;3)\)

Hàm số \(d_2\) qua \(C(0;-1);D(2;3)\)

Hàm số \(d_3\) qua \(E(0;3);F(3;0)\)

Vẽ đồ thị:

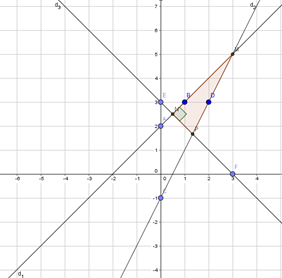
Dễ thấy bằng đồ thị, Tam giác MNP vuông tại N.

Vì N là giao điểm của \(d_1\) và \(d_3\)

Ta có tích hệ số góc của \(d_1\) và \(d_3\) là \(1.(-1)=-1\)

Vẽ đường thẳng \(y=6-x\) trên mặt phẳng tọa độ.

Chứng tỏ đường thẳng tạo với hai trục tọa độ và gốc tọa độ thành một tam giác vuông cân. Tính chu vi và diện tích của tam giác vuông cân ấy.

Hướng dẫn giải

Đường thẳng \(y=6-x\) đi qua các điểm \(A(1;5), B(2;4)\)

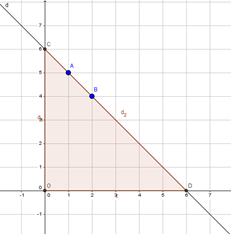
Chúng ta tìm điểm cắt trục tung của đường thẳng đó là điểm \(C(0;6)\)

Điểm cắt trục hoành là điểm \(D(6;0)\)

Ta có độ lớn đại số của \(OC=OD=6(dvdd)\)

Vậy tam giác OCD vuông cân tại O.

Áp dụng định lý Pytago vào tam giác vuông cân OCD, ta tìm được \(CD=\sqrt{OD^2+OC^2}=\sqrt{6^2+6^2}=6\sqrt{2}(dvdd)\)

Vậy, Chu vi của tam giác OCD là \(OC+OD+CD=12+6\sqrt{2}(dvdd)\)

Diện tích tam giác OCD là \(\frac{1}{2}OD.OC=\frac{1}{2}.6.6=18(dvdt)\)

Câu 1

a) Với những giá trị nào của m thì hàm số bậc nhất  \(y = (m – 1)x + 3\) đồng biến?

b) Với những giá trị nào của k thì hàm số bậc nhất \(y = (5 – k)x + 1\) nghịch biến? 

Câu 2: Tìm giá trị của a để hai đường thẳng \(y = (a – 1)x + 2 \,\,\,(a ≠ 1)\) và \(y = (3 – a)x + 1 \,\,\,(a ≠ 3)\) song song với nhau.

Câu 3: Cho hai hàm số bậc nhất \(y = \left( {k + 1} \right)x + 3\) và \(y = \left( {3 - 2k} \right)x + 1\).

a) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng song song với nhau?

b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau?

c) Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao? 

Câu 4: Với những giá trị nào của m thì đồ thị của các hàm số \(y = 12x + \left( {5 - m} \right)\) và \(y = 3x + \left( {3 + m} \right)\) cắt nhau tại một điểm trên trục tung ? 

Câu 5: Tìm giá trị của \(a\) để hai đường thẳng \(y = \left( {a - 1} \right)x + 2\) và \(y = \left( {3 - a} \right)x + 1\) song song với nhau.

Câu 1: Đường thẳng d đi qua gốc tọa độ và song song với đường thẳng AB có \(A(2;1);B(1;3)\) có phương trình là:

A. \(y=2x\)

B. \(y=-2x\)

C. \(y=-2x+2\)

D. \(y=2x+2\)

Câu 2: Không vẽ đồ thị, hãy cho biết đa giác được tạo bởi 4 đường thẳng sau là hình gì?

\(d_1:y=2x+1;d_2:y=2x-3;d_3: y=\frac{-1}{2}x+6;d_4:y=\frac{-1}{2}x-1\)

 A. Tam giác đều

B. Hình bình hành

C. Hình chữ nhật

D. Hình thang cân

Câu 3: Cho hàm số bậc nhất \(y=ax+3\). Xác định hệ số góc a biết hàm số qua điểm \(A(2;2)\)

A. \(a=\frac{-1}{2}\)

B. \(a=\frac{1}{2}\)

C. \(a=1\)

D. \(a=-1\)

Câu 4: Với giá trị nào của m thì ba hàm số sau đây chỉ có 2 giao điểm?

\(d_1: y=2x-3; d_2: y=2x+m; d_3: y=5x-m^2\)

A. \(m=0\)

B. \(m= -3\)

C. \(m\neq -3\)

D. \(m\neq 0\)

Câu 5: Cho hai đường thẳng \(y=mx+4\) và \(y=(m-1)x+3\)

Giá trị của m để hai đường thẳng vuông góc với nhau là:

A. \(m=-1\)

B. \(m=2\)

C. \(m\neq 0\)

D. Không có m thỏa bài toán

Qua bài học này giúp học sinh:

• Hệ thống hóa kiến thức cơ bản của chương.
• Hiểu các khái niệm hàm số, đồ thị của hàm số, khái niệm hàm số bậc nhất y =ax+b, tính chất đồng biến, nghịch biến của hàm số bậc nhất.
• Vẽ thành thạo đồ thị hàm số bậc nhất, xác định góc của đường thẳng y = ax+b và chiều dương của trục Ox.