Toán 9 Ôn tập chương 4: Hình trụ - Hình nón - Hình cầu
Nội dung Ôn tập chương 4 sẽ giúp các em học sinh tổng hợp lại kiến thức trong cả chương với một số bài tập cơ bản nhằm mục đích ôn luyện. Hi vọng bài giải sẽ là nguồn tài liệu giúp ích các em.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Hình trụ
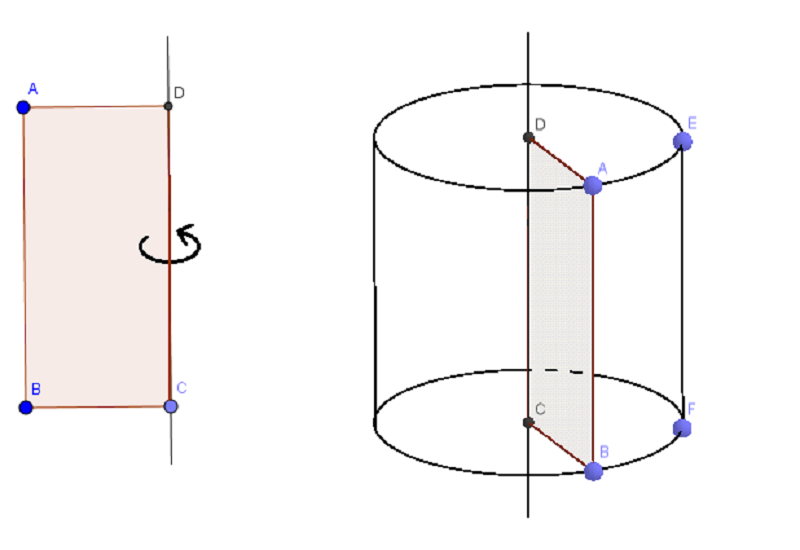
a. Diện tích xung quanh hình trụ
Với bán kính đáy r và chiều cao h, ta có:
Diện tích xung quanh: \(S_{xq}=2\pi rh\)
Diện tích toàn phần: \(S_{tp}=2\pi rh+2\pi r^2\)
b. Thể tích hình trụ
Thể tích hình trụ được cho bởi công thức: \(V=Sh=\pi r^2h\)
1.2. Hình nón
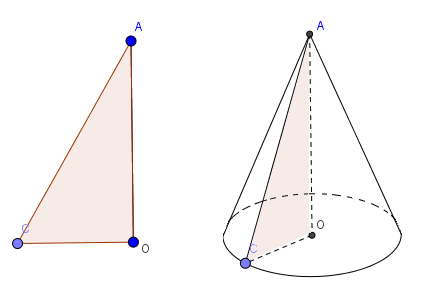
a. Diện tích xung quanh của hình nón
Công thức: \(S_{xq}=\pi rl\)
Trong đó: r là bán kính của đáy; l là độ dài đường sinh
Vậy ta suy ra công thức diện tích toàn phần:
\(S_{tp}=S_{xq}+S_{day}=\pi rl+\pi r^2\)
b. Thể tích hình nón
Bằng thực nghiệm, ta có thể tích hình nón là: \(V=\frac{1}{3}\pi r^2h\)
1.3. Hình nón cụt
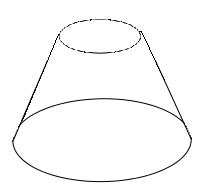
Diện tích xung quanh và thể tích hình nón cụt
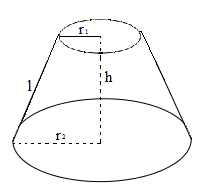
Ta có các công thức sau:
\(S_{xq}=\pi (r_1+r_2)l\)
\(V=\frac{1}{3}\pi h(r_{1}^{2}+r_{2}^{2}+r_1r_2)\)
1.4. Hình cầu
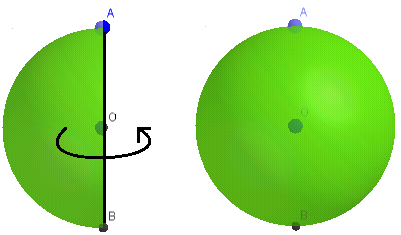
a. Diện tích mặt cầu
Nhắc lại kiến thức đã học ở lớp dưới, ta có công thức sau:
\(S=4\pi R^2=\pi d^2\) (với R là bán kính, d là đường kính của mặt cầu)
b. Thể tích mặt cầu
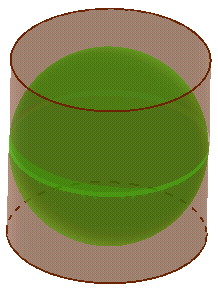
Công thức tính thể tích mặt cầu:
\(V=\frac{4}{3}\pi R^3\)
2. Bài tập minh hoạ
2.1. Bài tập 1
Hình trụ có chu vi đường tròn là \(20\pi cm\), chiều cao là \(4cm\). Thể tích hình trụ là:
Hướng dẫn giải
Từ chu vi của đường tròn, ta suy ra \(R=10 cm\); Vậy Thể tích là \(V=\pi R^2h=\pi.10^2.4=400 \pi (cm^3)\)
2.2. Bài tập 2
Cho hình vẽ
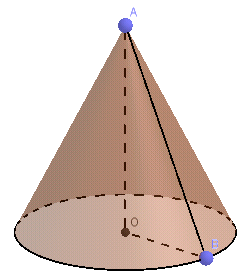
Cho biết \(OB=5cm, AB=13cm\). Thể tích của hình nón trên là:
Hướng dẫn giải
Bằng định lí Pytago, ta suy ra được \(OA=\sqrt{AB^2-OB^2}=12cm\)
Vậy \(V=\frac{1}{3}.OA.\pi.OB^2=\frac{1}{3}.12.5^2.\pi=100 \pi(cm^3)\)
2.3. Bài tập 3
Diện tích xung quanh của hình nón cụt có bán kính đáy lớn đáy nhỏ lần lượt là \(14cm, 8cm\) và có đường sinh bằng \(9cm\) là:
Hướng dẫn giải
\(S_{xq}=\pi(R+r)l=\pi(14+8).9=198\pi (cm^2)\)
2.4. Bài tập 4
Mô tả hình bên được tạo nên bởi một hình nón có đường sinh là \(13cm\), bán kính là \(5cm\) và một nửa mặt cầu. Hãy tính thể tích khối hình.

Hướng dẫn giải
Dễ dàng tính được đường cao của hình nón bằng định lí Pytago: \(h=\sqrt{13^2-5^2}=12cm\)
Vậy thể tích của hình nón là: \(V_{non}=\frac{1}{3}\pi R^2h=\frac{1}{3}\pi.5^2.12=100\pi (cm^3)\)
Thể tích nửa mặt cầu là: \(V_(nuacau)=\frac{2}{3}\pi R^3=\frac{2}{3}\pi.5^3=\frac{250}{3}\pi(cm^3)\)
Vậy thể tích khối hình là \(100\pi+\frac{250}{3}\pi=\frac{550}{3} \pi(cm^3)\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Độ dài các cạnh của một tam giác \(ABC\) vuông tại \(A\), thỏa mãn các hệ thức sau:
\(BC = AB + 2a \) (1)
\(\displaystyle AC = {1 \over 2}\left( {BC + AB} \right)\) (2)
\(a\) là một độ dài cho trước
a) Tính theo \(a\), độ dài các cạnh và chiều cao \(AH\) của tam giác.
b) Tam giác \(ABC\) nội tiếp được trong nửa hình tròn tâm \(O.\) Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó.
c) Cho tam giác \(ABC\) quay một vòng quanh cạnh huyền \(BC.\) Tính tỉ số diện tích giữa các phần do các dây cung \(AB\) và \(AC\) tạo ra.
Câu 2: Với một hình nón có bán kính đường tròn đáy là \(r (cm)\) và chiều cao \(2r (cm)\) và một hình cầu bán kính \(r (cm).\) Hãy tính:
a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là \(21,06 \;\left( {c{m^2}} \right)\).
b) Thể tích hình nón, biết thể tích hình cầu là \(15,8 \;\left( {c{m^3}} \right)\)
Câu 3: Với nửa hình cầu bán kính \(r\) và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng \(h\).
a) Khi \(r = 12\; (cm)\) và thể tích hai hình bằng nhau thì giá trị \(h\; (cm)\) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu?
b) Khi \(h = 12\, (cm)\) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì \(r (cm)\) bằng bao nhiêu?
Câu 4: Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h (cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?
3.2. Bài tập trắc nghiệm
Câu 1: Cho bán kính của Trái Đất và Mặt Trăng tương ứng là \(6371\) và \(1738\) kilomet. Trong các số sau đây, số nào là tỉ số thể tích giữa Trái Đất và Mặt Trăng?
(A) \(3,67\) (C) \(15,63\)
(B) \(4,93\) (D) \(49,26\).
Câu 2: Tỷ số thể tích của hình nón nội tiếp hình trụ và hình trụ là? (biết rằng chiều cao của nón bằng \(\frac{1}{2}\) đường cao hình trụ)
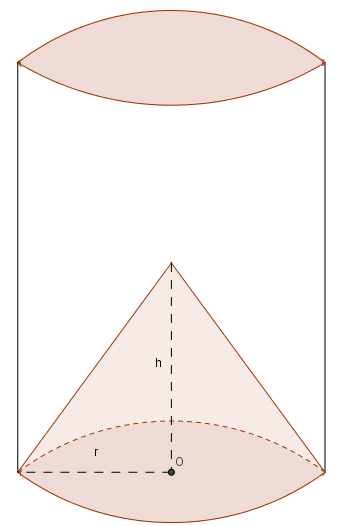
A. \(\frac{1}{3}\)
B. \(\frac{1}{6}\)
C. \(\frac{1}{9}\)
D. \(\frac{1}{12}\)
Câu 3: Hình sinh ra khi quay quanh cạnh FI là:
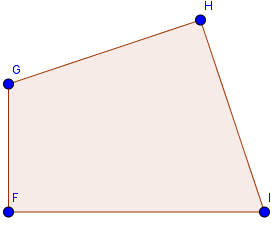
A. Hình trụ
B. Hình hộp chữ nhật
C. Hình nón và hình trụ
D. Hình nón và hình chóp cụt
Câu 4: Thể tích của khối hình trên là: (biết bán kính đáy là 5, đường cao hình nón là 12)
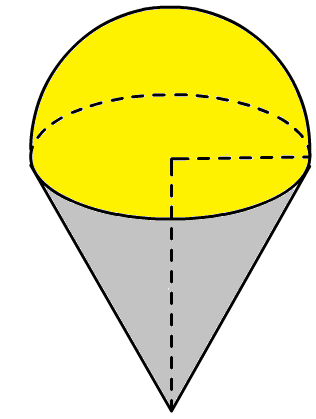
A. \(\frac{250\pi}{3}\)
B. \(\frac{310\pi}{3}\)
C. \(\frac{125\pi}{3}\)
D. \(\frac{155\pi}{3}\)
Câu 5: Một hình khối được mô tả như hình bên:

Được cấu tạo bởi một hình trụ và hai nửa mặt cầu hai bên. Biết hình trụ có chiều dài là \(20\), bán kính mặt đáy hình trụ là \(4\). Hãy tính diện tích toàn phần của hình khối.
A. \(56 \pi\)
B. \(64 \pi\)
C. \(120 \pi\)
D. \(184 \pi\)
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Nhớ và khắc sâu các khái niệm về hình trụ ( đáy, trục, mặt xung quanh, đường sinh độ dài đường cao, mặt cắt . . của hình trụ ) .
- Nắm chắc và biết sử dụng công thức tính diện tích xung quanh , diện tích toàn phần , thể tích của hình trụ .
