Toán 9 Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
Mời các em học sinh tham khảo lý thuyết góc tạo bởi tiếp tuyến và dây cung đã được eLib biên soạn dưới đây, cùng với phần tổng hợp kiến thức cơ bản cần nắm, đây sẽ tài liệu hữu ích cho các em học tốt môn Toán lớp 9.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khái niệm
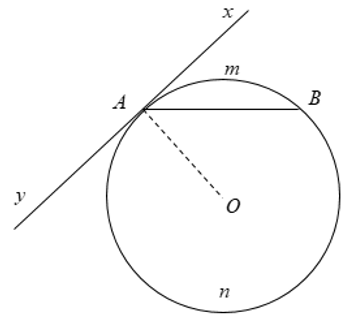
Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.
Cung nằm bên trong là cung bị chắn.
Hình vẽ trên ta có: góc \(\widehat{BAx}\) (hoặc \(\widehat{BAy}\)) là góc tạo bởi tiếp tuyến và dây cung.
1.2. Định lí
Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn
Cụ thể ở hình trên, \(\widehat{BAx}=\frac {1}{2}\)sđ\(\stackrel\frown{AB}\) (ở đây là cung AB nhỏ)
1.3. Hệ quả
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
2. Bài tập minh hoạ
2.1. Bài tập cơ bản
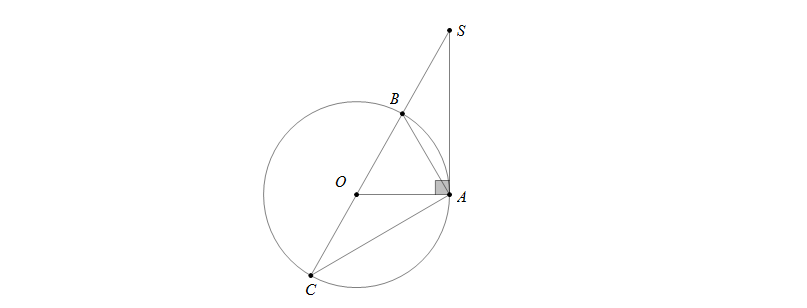
Câu 1: Cho đường tròn \((O;R)\) và điểm \(A\) trên đường tròn, tiếp tuyến tại \(A\) cắt đường kính \(BC\) của đường tròn tại \(S\). Biết \(\widehat{SAB}=30^0\), tính \(AC\) theo \(R\).
Hướng dẫn giải
Ta có \(\widehat{SAB}+\widehat{BAO}=90^0 \Rightarrow \widehat{BAO}=90^0-30^0=60^0\)
\(\bigtriangleup OBA\) cân tại \(O\) có \(\widehat{BAO}=60^0\) nên \(\bigtriangleup BAO\) đều. Suy ra \(BA=OB=R\)
Áp dụng định lí Pytago cho tam giác vuông \(ABC\) ta có \(AC=\sqrt{BC^2-AB^2}=\sqrt{(2R)^2-R^2}=\sqrt{3R^2}=R\sqrt{3}\)
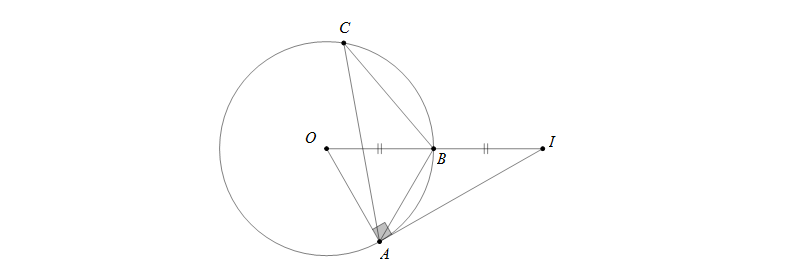
Câu 2: Cho đường tròn \((O;R)\) và điểm \(I\) nằm ngoài đường tròn sao cho \(OI=2R\). Điểm \(C\) nằm trên đường tròn. Vẽ tiếp tuyến \(IA\) của đường tròn, gọi \(B\) là giao điểm của \(OI\) và \((O)\) (\(B\) nằm giữa \(O\) và \(I\)). Tính \(\widehat{ACB}\)
Hướng dẫn giải
Ta có \(BI=OI-OB=2R-R=R\)
Tam giác vuông \(AOI\) có \(B\) là trung điểm của \(OI\) nên \(BA=BO=BI=R\) suy ra \(\bigtriangleup OBA\) đều (các cạnh đều bằng \(R\))
nên \(\widehat{BOA}=60^0 \Rightarrow \widehat{ACB}=30^0\)
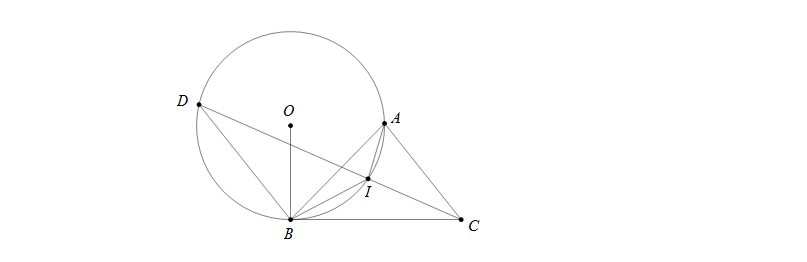
Câu 3: Cho tam giác ABC, vẽ đường tròn tâm O đi qua A và tiếp xúc với BC tại B. Kẻ dây BD song song với AC. Gọi I là giao điểm của CD với đường tròn. Chứng minh: \(\widehat{IAB}=\widehat{ICA}=\widehat{IBC}\)
Hướng dẫn giải
Theo hệ quả định lí góc tạo bởi tiếp tuyến và dây cung ta có \(\widehat{IAB}=\widehat{IBC}=\widehat{IDB}\) (cung chắn \(\stackrel\frown{IB}\))
Mặt khác, \(\widehat{IDB}=\widehat{ICA}\) (do \(BD//AC\))
Từ (1) và (2) suy ra \(\widehat{IAB}=\widehat{ICA}=\widehat{IBC}\) (đpcm)
2.2. Bài tập nâng cao
Câu 1: Cho đường tròn \((O)\) và điểm \(M\) nằm ngoài đường tròn, từ \(M\) vẽ cát tuyến \(MAB\) đến đường tròn. \(C\) là điểm trên đường tròn khác \(A\) và \(B\). Chứng minh rằng: \(MC\) là tiếp tuyến của đường tròn \((O)\) khi và chỉ khi \(MC^2=MA.MB\)
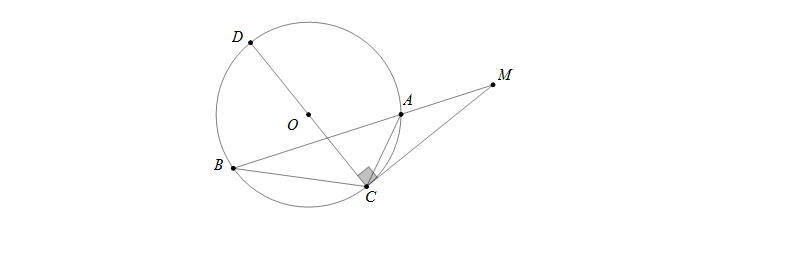
Hướng dẫn giải
Chiều thuận: \(MC\) là tiếp tuyến với đường tròn suy ra \(\widehat{MCA}=\widehat{MBC}\)
Xét \(\bigtriangleup MAC\) và \(\bigtriangleup MCB\) có \(\widehat{M}\) chung và \(\widehat{MCA}=\widehat{MBC}\) nên \(\bigtriangleup MAC \sim \bigtriangleup MCB\) (g.g)
suy ra \(\frac{MA}{MC}=\frac{MC}{MB} \Rightarrow MC^2=MA.MB\)
Chiều đảo: \(MC^2=MA.MB \Rightarrow \frac{MA}{MC}=\frac{MC}{MB}\)
Xét \(\bigtriangleup MAC\) và \(\bigtriangleup MCB\) có \(\widehat{M}\) chung và \(\frac{MA}{MC}=\frac{MC}{MB}\) nên \(\bigtriangleup MAC \sim \bigtriangleup MCB\) (c.g.c)
suy ra \(\widehat{MCA}=\widehat{MBC} \Rightarrow \widehat{MCA}=\frac{1}{2}\)sđ\(\stackrel\frown{AC}\)
Kẻ đường kính \(CD\) khi đó \(\widehat{MCA}+\widehat{ACD}=\frac{1}{2}\)\(\widehat{MCD}=\widehat{MCA}+\widehat{ACD}=\frac{1}{2}\)sđ\(\stackrel\frown{AC}\)+\(\frac{1}{2}\)sđ\(\stackrel\frown{AD}\)=\(90^0\)
Từ đó suy ra \(MC\) là tiếp tuyến của đường tròn \((O)\)
Câu 2: Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Tiếp tuyến tại \(A\) của đường tròn \((O')\) cắt \((O)\) tại \(C\) và đối với đường tròn \((O)\) cắt \((O')\) tại \(D\).
Chứng minh \(AB^2=BD.BC\)
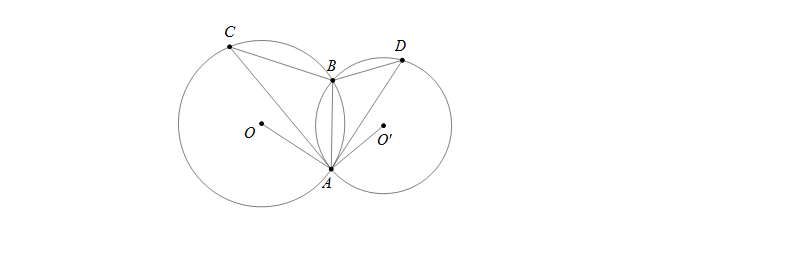
Hướng dẫn giải
Trong đường tròn \((O)\) ta có \(\widehat{ACB}=\widehat{BAD}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung chùng chắn cung \(BA\))
Tương tự trong đường tròn \((O')\) ta cũng có \(\widehat{BDA}=\widehat{BAC}\)
Xét \(\bigtriangleup CAB\) và \(\bigtriangleup ADB\) có \(\widehat{ACB}=\widehat{BAD}\) và \(\widehat{BDA}=\widehat{BAC}\)
nên \(\bigtriangleup CAB\sim \bigtriangleup ADB\) suy ra \(\frac{CB}{AB}=\frac{AB}{DB}\Rightarrow AB^2=BD.BC\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’))
a. Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì 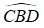
b. Từ C và D vẽ hai tiếp tuyến với đường tròn.Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Câu 2: Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó
a. Chứng minh rằng luôn có MT2= MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b. Cho MT = 20cm ,MB = 50cm,tính bán kính đường tròn
Câu 3: Ngồi trên đỉnh núi cao 1 km thì có thể nhìn thấy một địa điểm T trên mặt đất với khoảng cách tối đa là bao nhiêu ? Biết rằng bán kính Trái Đất gần bằng 6400 km
Câu 4: Cho tam giác ABC nội tiếp trong đường tròn (O).Vẽ tia Bx sao cho tia BC nằm giữa hai tia Bx,BA và 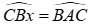
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I. Biết AB=20cm, AC=28cm, BC=24cm. Khi đó IA bằng bao nhiêu cm?
A. 32cm
B. 20cm
C. 28cm
D. 35cm
Câu 2: Trong các khẳng định sau, khẳng định nào đúng:
A. Góc tạo bởi tia tiếp tuyến và dây cung luôn nhỏ hơn 900.
B. Góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp luôn bằng nhau.
C. Số đo góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo góc ở tâm cùng chắn cung đó.
D. Góc tạo bởi hai dây cung của một đường tròn luôn luôn bé hơn 900.
Câu 3: Khẳng định nào sau đây là sai:
A. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn
B. Trong một đường tròn, số đo góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
C. Nếu góc BAx có số đo bằng nửa số đo của cung BA nằm ngoài góc đó thì Ax là một tia tiếp tuyến của đường tròn chứa cung AB.
D. Với MAB là cát tuyến và T là một điểm trên đường tròn, từ hệ thức MT2=MA.MB ta suy ra MT là tiếp tuyến của đường tròn đó.
Câu 4: Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Tiếp tuyến tại \(A\) của đường tròn \((O')\) cắt \((O)\) tại \(C\) và đối với đường tròn \((O)\) cắt \((O')\) tại \(D\). Biết rằng BC=16cm, BD=12cm. Độ dài BA là:
A. \(8\sqrt{3} cm\)
B. \(10 cm\)
C. \(8\sqrt{2} cm\)
D. \(8 cm\)
Câu 5: Cho đường tròn (O;R), điểm A nằm ngoài đường tròn và OA=2R. Từ A vẽ hai tiếp tuyến AB,AC đến đường tròn (O). Gọi H là giao điểm của BC và OA. Khi đó, điều nào sai trong các điều sau:
A. \(\bigtriangleup ABC\) đều
B. \(AO\perp BC\)
C. \(HO=\frac{R}{2}\)
D. \(BC=R\sqrt{2}\)
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Nhận biết được góc tạo bởi tia tiếp tuyến và dây cung.
- Phát biểu và chứng minh được định lí về số đo góc tạo bởi tia tiếp tuyến và dây cung trong 3 trường hợp.
- HS phân chia được các trường hợp để tiến hành chứng minh.
Tham khảo thêm
- doc Toán 9 Chương 3 Bài 1: Góc ở tâm và số đo cung
- doc Toán 9 Chương 3 Bài 2: Liên hệ giữa cung và dây
- doc Toán 9 Chương 3 Bài 3: Góc nội tiếp
- doc Toán 9 Chương 3 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- doc Toán 9 Chương 3 Bài 6: Cung chứa góc
- doc Toán 9 Chương 3 Bài 7: Tứ giác nội tiếp
- doc Toán 9 Chương 3 Bài 8: Đường tròn ngoại tiếp và đường tròn nội tiếp
- doc Toán 9 Chương 3 Bài 9: Độ dài đường tròn, cung tròn
- doc Toán 9 Chương 3 Bài 10: Diện tích hình tròn, hình quạt tròn
- doc Toán 9 Ôn tập chương 3: Góc với đường tròn