Toán 9 Chương 4 Bài 2: Đồ thị của hàm số \(y = ax^2\) (a ≠ 0)
Để giúp các em học sinh lớp 9 học hiệu quả môn Toán, đội ngũ eLib đã biên soạn và tổng hợp nội dung bài Đồ thị của hàm số \(y = ax^2\). Tài liệu gồm kiến thức cần nhớ và các dạng Toán về đồ thị, giúp các em học tập và củng cố thật tốt kiến thức. Mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Nhắc lại kiến thức
Như ta đã biết, trên mặt phẳng tọa độ, đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.
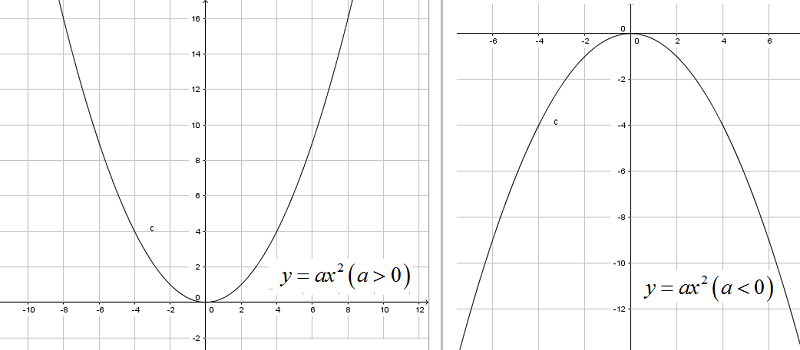
1.2. Cách vẽ đồ thị
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ \(5\) đến \(7\) giá trị) tương ứng giữa \(x\) và \(y.\)
Bước 3: Vẽ đồ thị và kết luận
Chú ý
Vì đồ thị \(y=ax^2 (a\neq 0)\) luôn đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng nên để vẽ đồ thị này, ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy đối xứng của chúng qua Oy.
2. Bài tập minh họa
2.1. Bài tập cơ bản
Câu 1: Cho hàm số \(y=\frac{1}{2}x^2\). Các điểm \(A(1;\frac{1}{2})\); \(B(2;4)\); \(C(3;4,5)\) có thuộc đồ thị hàm số trên không? Vì sao?
Hướng dẫn giải
Lần lượt lấy tọa độ các điểm A, B, C thay vào đồ thị hàm số trên, ta có điểm A và C thuộc hàm số, C không thuộc hàm số
Câu 2: Cho hàm số \(y=ax^2 (a\neq 0)\). Biết điểm \(A(3;3)\) thuộc hàm số đó. Xác định hệ số a.
Hướng dẫn giải
Do hàm số \(y=ax^2 (a\neq 0)\) đi qua điểm \(A(3;3)\) nên thế tọa độ điểm A vào x và y, ta được: \(3=a.3^2\Rightarrow a=\frac{1}{9}\)
Câu 3: Cho hàm số \(y=-2x^2\) và đường thẳng \(y=-3x+1\). Tìm giao điểm của hai đồ thị đó bằng hình vẽ và đồ thị
Hướng dẫn giải
Vẽ hình HS tự vẽ.
Tìm giao điểm: Phương trình hoành độ giao điểm: \(-2x^2=-3x+1\Leftrightarrow 2x^2-3x+1=0\Leftrightarrow\)
\(x=1\Rightarrow y=-2; x=\frac{1}{2}\Rightarrow y=\frac{-1}{2}\)
2.2. Bài tập nâng cao
Câu 1: Cho hàm số \(y=2x^2\). Tìm giá trị nhỏ nhất của y khi x đi từ -2017 đến 2018
Hướng dẫn giải
Ta thấy hệ số a của đồ thị này dương, nên đồ thị có giá trị nhỏ nhất \(y=0\) tại \(x=0\).
Nhận thấy rằng trong khoảng -2017 đến 2018 đi qua hoành độ \(x=0\) nên giá trị nhỏ nhất của hàm số \(y=2x^2\) là \(y(0)=0\)
Câu 2: Cho hàm số \(y=-\frac{1}{4}x^2\). Tìm giá trị nhỏ nhất của y khi x đi từ -1 đến 2
Hướng dẫn giải
Hệ số a của đồ thị này âm nên đồ thị có giá trị cao nhất là \(y=0\). Khi x càng tiến về dương hoặc âm vô cùng, giá trị của y sẽ càng nhỏ dần.
Ta thấy \(|-1|<|2|\Rightarrow y(-1)>y(2)\). Vậy, giá trị nhỏ nhất của y thỏa bài toán là \(y(min)=y(2)=-\frac{1}{4}.2^2=-1\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho ba hàm số: \(y=\frac{1}{2}x^2; y = x^2 ; y = 2x^2\)
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm A', B', C' có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A', B và B', C và C'.
d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.
Câu 2: Cho hàm số \(y = f(x) = x^2\)
a) Vẽ đồ thị của hàm số đó
b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5)
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3};\sqrt{7}\)
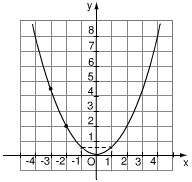
Câu 3: Biết rằng đường cong trong hình 11 là một parabol y = ax2
a) Tìm hệ số a
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = -3
c) Tìm các điểm thuộc parabol có tung độ y = 8
Câu 4: Cho hai hàm số \(y = \frac{1}{3}x^2\) và \(y = -x + 6.\)
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ các giao điểm của hai đồ thị đó
3.2. Bài tập trắc nghiệm
Câu 1: Tọa độ giao điểm của phương trình hàm số \(y=x^2\) và đường thẳng \(y=4x-3\) là:
A. \((-1;1), (3;9)\)
B. \((-1;1), (-3;9)\)
C. \((1;1), (3;9)\)
D. \((1;1), (-3;9)\)
Câu 2: Giá trị nhỏ nhất của hàm số \(y=-2x^2\) khi \(x\epsilon [-8;3]\) là:
A. 0
B. -32
C. -64
D. -128
Câu 3: Đồ thị hàm số \(y=\frac{1}{3}x^2\) đi qua điểm nào sau đây:
A. \(A\left ( 1;0 \right )\)
B. \(C\left ( \frac{1}{3};\frac{1}{9} \right )\)
C. \(B\left ( \frac{1}{3};\frac{1}{27} \right )\)
D. \(D\left ( \frac{1}{4};\frac{1}{16} \right )\)
Câu 4: Số giao điểm đồ thị hàm số \(y=4x^2\) và đồ thị đường thẳng \(y=4x-3\) là:
A. 1
B. 0
C. 2
D. 3
Câu 5: Giá trị lớn nhất của đồ thị hàm số \(y=4x^2\) trên đoạn \(x\epsilon [-5;1]\) là:
A. 64
B. 100
C. 144
D. 196
4. Kết luận
Qua bài học này giúp học sinh:
- Mô tả được hình dạng của đồ thị hàm số \(y=ax^2 (a\neq 0)\) và phân biệt được chúng trong hai trường hợp a>0; a<0.
- Phát biểu được tính chất của đồ thị và liên hệ được tính chất của đồ thị với tính chất của hàm số \(y=ax^2 (a\neq 0)\)
- Làm được bài tập có liên quan.
- Vẽ chính xác đồ thị hàm số \(y=ax^2 (a\neq 0)\)
Tham khảo thêm
- doc Toán 9 Chương 4 Bài 1: Hàm số \(y = ax^2\) (a ≠ 0)
- doc Toán 9 Chương 4 Bài 3: Phương trình bậc hai một ẩn
- doc Toán 9 Chương 4 Bài 4: Công thức nghiệm của phương trình bậc hai
- doc Toán 9 Chương 4 Bài 5: Công thức nghiệm thu gọn
- doc Toán 9 Chương 4 Bài 6: Hệ thức Vi-ét và ứng dụng
- doc Toán 9 Chương 4 Bài 7: Phương trình quy về phương trình bậc hai
- doc Toán 9 Chương 4 Bài 8: Giải bài toán bằng cách lập phương trình
- doc Toán 9 Ôn tập chương 4: Phương trình bậc hai một ẩn
