Toán 9 Chương 1 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời

a) Nhiệm vụ: Xác định chiều cao của một tòa tháp mà không cần lên đỉnh tháp

b) Chuẩn bị: Giác kế, thước cuộn, máy tính bỏ túi

c) Hướng dẫn thực hiện:

- Đặt giác kế thẳng đứng cách tháp một khoảng \(a\), chiều cao của giác kế là \(b\).

- Quay thanh giác kế sao cho khi ngắm theo thanh này ta nhìn thấy đỉnh của tháp. Đọc số đo của góc trên giác kế là \(\alpha\).

- Dùng máy tính tính \(tan\alpha\). Khi đó ta có chiều cao của tháp là: \(b+a.tan\alpha\)

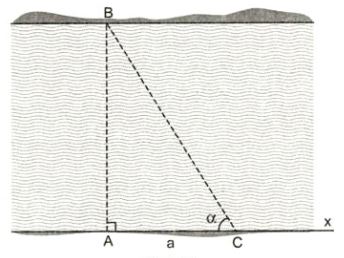
a) Nhiệm vụ: Xác định chiều rộng một khúc sông mà việc đo đạc chỉ tại 1 bờ sông

b) Chuẩn bị: Ê-ke đạc, giác kế, thước cuộn, máy tính bỏ tính hoặc bảng lượng giác

c) Hướng dẫn thực hiện:

-Chọn một điểm bên kia sông sát bờ sông đặt là B, lấy một điểm bên này sông sát bờ. 

-Kẻ 1 đường thẳng bên này sông sao cho vuông góc với AB. lấy 1 điểm C trên đường thẳng vuông góc vừa vẽ

- Đoạn \(AC=a\) dùng giác kế đo\(\widehat{ACB}=\alpha\) . Khi đó chiều rộng khúc sông chính là giá trị của: \(a.tan\alpha\)

Câu 1. Tính chiều cao của một cây xanh biết rằng một người cao 1,7m đứng nhìn lên đỉnh cây thì hướng nhìn tạo với mặt đất góc 35 độ và khoảng cách từ người đó đến cây là 20m

Hướng dẫn giải

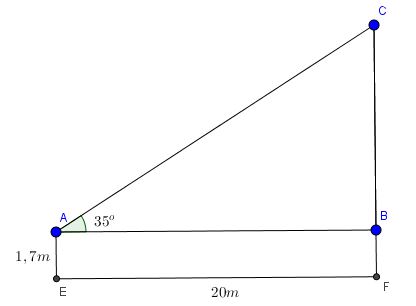
Ta xem đề bài giống như hình vẽ trên \(\widehat{ABC}=90^{\circ}\)

Khi đó chiều cao cây cần tính là đoạn: \(CF=CB+BF=AB.tan35^{\circ}+AE=20.tan35^{\circ}+1,7\simeq 15,7 (m)\)

Câu 2. Một cái cây bị sét đánh trúng giữa thân cây làm thân cây ngã xuống đất tạo với mặt đất một góc là \(40^{\circ}\). Biết rằng khúc thân cây còn đứng cao 3m.

Tính chiều cao lúc đầu của cây

Hướng dẫn giải

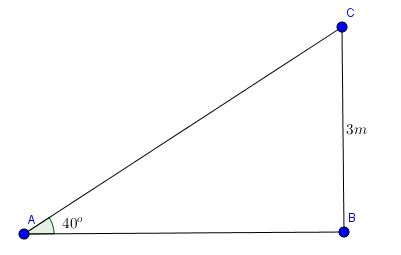
Ta xem đề bài như hình vẽ với \(\widehat{ABC}=90^{\circ}\)

Khi đó chiều dài cây lúc đầu chính là: \(BC+AC=BC+\frac{BC}{sinA}=3.(1+\frac{1}{sin40^{\circ}})\simeq 7,67(m)\)

Câu 3. Một chiếc thang gấp đôi dài 6m được người ta sử dụng để leo lên một mái nhà. Biết rằng lúc leo lên mỗi chân thang tạo với mặt đất góc 60 độ. Tính chiều cao của căn nhà đó

Hướng dẫn giải

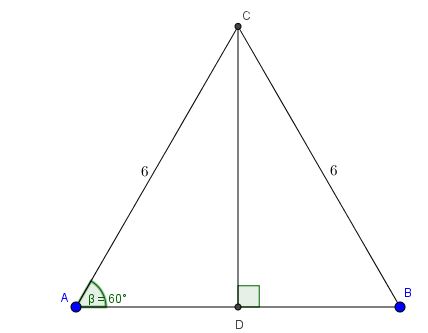
Ta xem đề bài như hình vẽ trên

Khi đó ta có \(\Delta ABC\) đều và \(CD=AC.sin60^{\circ}=6.\frac{\sqrt{3}}{2}=3\sqrt{3}\)

Một người quan sát ở hải đăng cao 88 feet (đơn vị đo lường Anh) so với mặt nước biển nhìn chiếc tàu ở xa với góc \(0{}^\circ 42'\). Hỏi khoảng cách từ tàu đến chân hải đăng tính theo đơn vị hải lí là bao nhiêu?

Hướng dẫn giải

Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc \(0{}^\circ 42'\), khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn.

Vậy khoảng cách từ tài đến chân ngọn hải đăng là:

\(80.\cot 0{}^\circ 42'\approx 6547,76\,(feet)\approx 1,24\) (hải lí).

Câu 1. Thang AB dài 6m  tựa vào tường làm thành góc \(63{}^\circ \) với mặt đất. Hỏi chiều cao của cái thang đạt được so với mặt đất?

Câu 2. Làm dây kéo cờ: Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ (chiếu bởi ánh sáng mặt trời) dài 9m và góc nhìn mặt trời là \(41{}^\circ 38'\).

Câu 3. Đài quan sát Toronto, Ontario, Canada cao 533m. Ở một thời điểm nào đó vào ban ngày, mặt trời chiếu tạo với bóng dài 1000m. Hỏi lúc đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu?

Câu 1. Một cột đèn cao 5m. tại một thời điểm tia sáng mặt trời tạo với mặt đất 1 góc 60 độ. Hỏi bóng của cột đèn đó trên mặt đất dài bao nhiêu

A. \(\frac{5}{\sqrt{2}}\)          

B. \(\frac{5}{\sqrt{3}}\)

C. \(\frac{5}{2}\)             

D. \(\frac{10}{\sqrt{2}}\)

Câu 2. Một tòa nhà tại một thời điểm tia sáng mặt trời tạo với mặt đất 1 góc là 50 độ thì bóng tòa nhà trên mặt đất dài 7m.

Chiều cao của tòa nhà là: 

A. \(\simeq 4,5\)       

B. \(\simeq 5,36\)

C. \(\simeq 5,87\)     

D. \(\simeq 8,34\)

Câu 3. Cho tam giác ABC vuông tại B có BC=20, D là điểm thuộc cạnh AB sao cho \(\widehat{BCD}=50^{\circ}, \widehat{DCA}=15^{\circ}\)

Độ dài AD là: 

A. \(\simeq 20,78\)   

B. \(\simeq 2,805\)

C. \(\simeq 19,05\)   

D. \(\simeq 21\)

Câu 4. Một chiếc thuyền băng qua một con sông. Do nước chảy nên hướng đi của thuyền bị lệch góc 30 độ so với hướng đi thẳng qua bờ bên kia. Biết rằng vận tốc của thuyền là 3m/s và thuyền đi trong 3 phút. Chiều dài sông là bao nhiêu

A. \(270\sqrt{3}\)       

B. \(540\)

C. \(270\sqrt{2}\)       

D. \(540\sqrt{3}\)

Câu 5. Một người sử dụng một cái thang dài để leo lên một tòa nhà. Biết rằng bóng của tòa nhà khi tia sáng mặt trời tạo với mặt đất góc 45 độ là 3m và khoảng cách từ chân thang đến nhà là 1,5m. Tính góc tạo bới thang và mặt đất 

A. \(48^{\circ}14{}'\)  

B. \(72^{\circ}14{}'\)

C. \(26^{\circ}14{}'\)  

D. \(63^{\circ}26{}'\)

Qua bài học này, các em cần đạt được những yêu cầu sau:

• Nắm vững các hệ thức về cạnh và góc trong tam giác vuông.
• Vận dụng kiến thức để làm bài toán về giải tam giác vuông.