Toán 9 Ôn tập chương 4: Phương trình bậc hai một ẩn
Bài giảng dưới đây được eLib biên soạn kiến thức cụ thể và chi tiết, cùng các bài tập minh họa có hướng dẫn giải chi tiết, qua đó giúp các em nắm được kiến thức từ khái quát đến chi tiết để học tốt phần kiến thức này.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Đồ thị hàm số \(y=ax^2 (a\neq 0)\)
Đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.
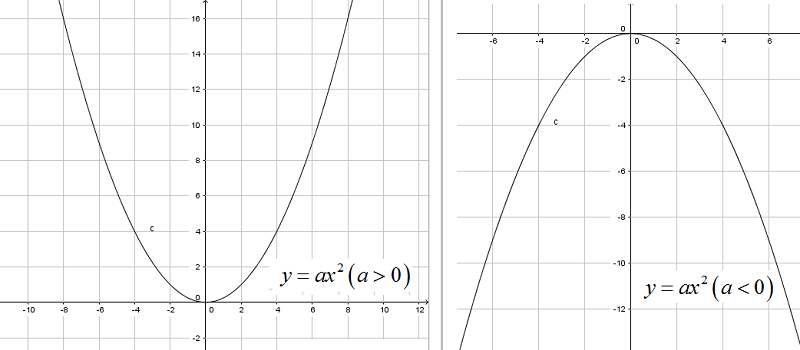
1.2. Phương trình bậc hai
Phương trình bậc hai một ẩn (gọi tắt là phương trình bậc hai) là phương trình có dạng \(ax^2+bx+c=0\)
Trong đó, x là ẩn; các hệ số a, b, c là các số cho trước và \(a\neq 0\)
1.3. Công thức nghiệm của phương trình bậc hai
Với phương trình \(ax^2+bx+c=0 (a\neq 0)\) và biệt thức \(\Delta =b^2-4ac\):
- \(\Delta>0\) thì phương trình có 2 nghiệm phân biệt:
- \(x_{1}=\frac{-b+\sqrt{\Delta }}{2a}\); \(x_{2}=\frac{-b-\sqrt{\Delta }}{2a}\)
- \(\Delta=0\) thì phương trình có nghiệm kép \(x=x_{1}=x_{2}=-\frac{b}{2a}\)
- \(\Delta<0\) phương trình vô nghiệm.
1.4. Công thức nghiệm thu gọn
Với các phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) và \(b=2b'\), \(\Delta '=b'^2-ac\) thì:
- Nếu \(\Delta '>0\) thì phương trình có hai nghiệm phân biệt: \(x_{1}=\frac{-b'+\sqrt{\Delta '}}{a}; x_{2}=\frac{-b'-\sqrt{\Delta '}}{a}\)
- Nếu \(\Delta '=0\) thì phương trình có nghiệm kép \(x=\frac{-b'}{a}\)
- Nếu \(\Delta '<0\) thì phương trình vô nghiệm.
1.5. Định lí Vi ét và ứng dụng
Phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) có 2 nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\Delta }}{2a}; x_2=\frac{-b-\sqrt{\Delta }}{2a}\)
Ta có: \(x_1+x_2=\frac{-2b+\sqrt{\Delta }-\sqrt{\Delta }}{2a}=-\frac{b}{a}\)
\(x_1.x_2=\frac{b^2-\Delta }{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)
Định lý Vi-ét
Nếu \(x_1;x_2\) là hai nghiệm của phương trình \(ax^2+bx+c=0 (a\neq 0)\) thì:
\(x_1+x_2=-\frac{b}{a}\) và \(x_1.x_2=\frac{c}{a}\)
Tổng quát
- Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a+b+c=0\) thì phương trình có một nghiệm là \(x_1=1\) và nghiệm kia là \(x_2=\frac{c}{a}\).
- Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a-b+c=0\) thì phương trình có một nghiệm là \(x_1=-1\) và nghiệm kia là \(x_2=-\frac{c}{a}\).
1.6. Các phương trình quy về phương trình bậc hai (phương trình trùng phương, phương trình có ẩn ở mẫu, phương trình tích...)
a. Phương trình trùng phương
Định nghĩa
Phương trình trùng phương là phương trình có dạng: \(ax^4+bx^2+c=0 (a\neq 0)\)
b. Phương trình chứa ẩn ở mẫu
Các bước để giải phương trình chứa ẩn ở mẫu đã học ở lớp 8
- Bước 1: Tìm điều kiện xác định của phương trình
- Bước 2: Quy đồng hai vế rồi khử mẫu
- Bước 3: Giải phương trình vừa nhận được
- Bước 4: So sánh điều kiện ban đầu rồi kết luận nghiệm
c. Phương trình tích
Nhắc lại kiến thức đã học ở lớp dưới:
Biến đổi phương trình về dạng \(A.B.C.....=0\) rồi suy ra hoặc \(A=0\) hoặc \(B=0\) hoặc.....
1.7. Giải toán bằng phương pháp lập phương trình
Phương pháp giải
Để giải bài toán bằng cách lập phương trình, chúng ta làm theo các bước sau:
Bước 1: Lập phương trình
- Chọn ẩn và đặt điều kiện cho ẩn
- Biểu đạt các đại lượng khác nhau theo ẩn
- Dựa vào đề bài toán, lập phương trình theo dạng đã học
Bước 2: Giải phương trình
Bước 3: So sánh kết quả tìm được và chọn nghiệm thích hợp
2. Bài tập minh họa
2.1. Bài tập 1
Cho hàm số \(y=-x^2\) và đường thẳng \(y=-4x+4\). Tìm giao điểm của hai đồ thị đó bằng hình vẽ và đồ thị
Hướng dẫn giải
Vẽ hình HS tự vẽ.
Tìm giao điểm: Phương trình hoành độ giao điểm: \(-x^2=-4x+4\Leftrightarrow x^2-4x+4=0\)
Tính biệt thức \(\Delta=0\) suy ra phương trình có nghiệm kép \(x=2\)
Vậy khi vẽ hình, ta chỉ nhận được một giao điểm. Sau này lên cấp trên, các em sẽ được biết đường thẳng trên là tiếp tuyến của hàm số.
2.2. Bài tập 2
Giải phương trình bằng cách phân tích đa thức thành nhân tử: \(x^2-11x-12=0\)
Hướng dẫn giải
\(x^2-11x-12=0\)
\(\Leftrightarrow x^2-12x+x-12=0\)
\(\Leftrightarrow x(x-12)+x-12=0\)
\(\Leftrightarrow (x+1)(x-12)=0\)
Vậy phương trình trên có hai nghiệm phân biệt là \(x=-1;x=12\)
2.3. Bài tập 3
Giải phương trình: \(x^2+10x+25=0\); \(x^2-4x-9=0\)
Hướng dẫn giải
+ \(x^2+10x+25=0\)
\(\Delta =10^2-4.1.25=0\) \(\Rightarrow x=\frac{-0}{2}=-5\)
+ \(x^2-4x-9=0\)
\(\Delta =(-4)^2-4.1.(-9)=52\Rightarrow \sqrt{\Delta }=2\sqrt{13}>0\)
\(\Rightarrow x_{1}=\frac{-(-4)+2\sqrt{13}}{2}=2+\sqrt{13};x_{2}=\frac{-(-4)-2\sqrt{13}}{2}=2-\sqrt{13}\)
2.4. Bài tập 4
Tìm hai số biết hiệu của chúng là 5 và tích của chúng là 150
Hướng dẫn giải
Gọi hai số cần tim là a, b
Ta có \(\left\{\begin{matrix} a-b=5\\ ab=150 \end{matrix}\right.\)
Thế \(a=5+b\) vào phương trình tích, ta được \(b(b+5)=150\Leftrightarrow b^2+5b-150=0\)
\(\Rightarrow b=-15\) hoặc \(b=10\)
\(b=-15\Rightarrow a=-10\)
\(b=10\Rightarrow a=15\)
2.5. Bài tập 5
Giải phương trình trùng phương sau: \(x^4-4x^2-5=0\)
Hướng dẫn giải
Đặt \(t=x^2 (t\geq 0)\)
Khi đó, phương trình trở thành: \(t^2-4t-5=0\)
Giải phương trình bậc hai cơ bản trên, ta được:
\(t=-1\) (loại)
\(t=5\) (nhận)\(\Rightarrow x=\pm \sqrt{5}\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hai hàm số: \(y = 2x - 3\) và \(y = - {x^2}\)
a) Vẽ đồ thị của hai hàm số này trong cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
Kiểm nghiệm rằng tọa độ của mỗi giao điểm đều là nghiệm chung của hai phương trình hai ẩn \(y = 2x – 3 \) và \(y = - {x^2}\)
Câu 2: Giải các phương trình:
a) \(3{x^2} + 4\left( {x - 1} \right) = {\left( {x - 1} \right)^2} + 3\)
b) \({x^2} + x + \sqrt 3 = \sqrt 3 x + 6\)
c) \(\displaystyle{{x + 2} \over {1 - x}} = {{4{x^2} - 11x - 2} \over {\left( {x + 2} \right)\left( {x - 1} \right)}}\)
d) \(\displaystyle{{{x^2} + 14x} \over {{x^3} + 8}} = {x \over {x + 2}}\)
Câu 3: Giải các phương trình trùng phương
a) \({x^4} + 2{x^2} - x + 1 = 15{x^2} - x - 35\)
b) \(2{x^4} + {x^2} - 3 = {x^4} + 6{x^2} + 3\)
c) \(3{x^4} - 6{x^2} = 0\)
d) \(5{x^4} - 7{x^2} - 2 = 3{x^4} - 10{x^2} - 3\)
Câu 4: Giải các phương trình sau bằng phương pháp đặt ẩn phụ:
a) \({\left( {{x^2} - 2x} \right)^2} - 2{x^2} + 4x - 3 = 0\)
b) \(3\sqrt {{x^2} + x + 1} - x = {x^2} + 3\)
3.2. Bài tập trắc nghiệm
Câu 1: Tập nghiệm của phương trình \(x^2< 100\) là:
A. \(x>-10\)
B. \(x>10\)
C. \(x<10\)
D. \(-10
Câu 2: Tổng và tích 2 nghiệm của phương trình \(x^2+2016x-2017=0\) lần lượt là:
A. \(S=-2016;P=-2017\)
B. \(S=2016;P=2017\)
C. \(S=-2016;P=2017\)
D. \(S=2016;P=-2017\)
Câu 3: Tọa độ giao điểm của phương trình hàm số \(y=x^2\) và đường thẳng \(y=8\) là:
A. \((0;0)\)
B. \((2\sqrt{2};0)\)
C. \((-2\sqrt{2};0)\)
D. \((-2\sqrt{2};0)(2\sqrt{2};0)\)
Câu 4: Với giá trị nào của m thì phương trình bậc hai \(x^2+6x-m=0\) vô nghiệm?
A. \(m<-9\)
B. \(m>-9\)
C. \(m>9\)
D. \(m<9\)
Câu 5: Tìm hai số biết tổng bằng 30 và tổng bình phương bằng 468.
A. \(14;16\)
B. \(17;13\)
C. \(18;12\)
D. \(19;11\)
4. Kết luận
Qua bài học này, học sinh cần:
- Có kỹ năng lập được bảng phân tích, biểu diễn các đại lượng trong bài toán theo ẩn số đã cho và các đại lượng đã biết
- Áp dụng đủ các bước giải để giải hoàn thiện bài toán bằng cách lập phương trình
- Vận dụng giải một số dạng toán cơ bản, không quá phức tạp .
- Làm được bài toán thực tế để thấy rõ toán học bắt nguồn từ thực tế cuộc sống và lại quay trở lại phục vụ thực tế.
Tham khảo thêm
- doc Toán 9 Chương 4 Bài 1: Hàm số \(y = ax^2\) (a ≠ 0)
- doc Toán 9 Chương 4 Bài 2: Đồ thị của hàm số \(y = ax^2\) (a ≠ 0)
- doc Toán 9 Chương 4 Bài 3: Phương trình bậc hai một ẩn
- doc Toán 9 Chương 4 Bài 4: Công thức nghiệm của phương trình bậc hai
- doc Toán 9 Chương 4 Bài 5: Công thức nghiệm thu gọn
- doc Toán 9 Chương 4 Bài 6: Hệ thức Vi-ét và ứng dụng
- doc Toán 9 Chương 4 Bài 7: Phương trình quy về phương trình bậc hai
- doc Toán 9 Chương 4 Bài 8: Giải bài toán bằng cách lập phương trình
