Giải bài tập SGK Toán 7 Bài 6: Mặt phẳng tọa độ

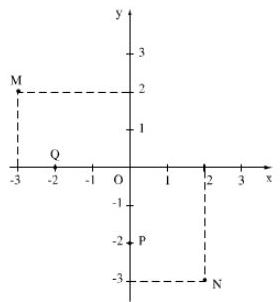
a) Viết toạ độ các điểm \(M, N,P,Q \) trong hình.

b) Em có nhận xét gì về toạ độ của các cặp điểm \(M\) và \(N\); \(P\) và \(Q\).

Phương pháp giải

- Cặp \(\left( {{x_0};{y_0}} \right)\) được gọi là tọa độ của điểm \(M \), trong đó \({{x_0}}\) là hoành độ và \({{y_0}}\) là tung độ của điểm \(M.\)

- Kí hiệu \(M\left( {{x_0};{y_0}} \right)\)

Hướng dẫn giải

Câu a: \(M(-3; 2); N(2; -3); Q(-2; 0); \)\(P(0; -2)\)

Câu b: Ta thấy hoành độ của điểm \(M\) chính là tung độ của điểm \(N\) và tung độ của điểm \(M\) chính là hoành độ của điểm \(N\). 

Hoành độ của điểm \(Q\) chính là tung độ của điểm \(P\) và tung độ của điểm \(Q\) chính là hoành độ của điểm \(P\).

Vẽ một hệ trục toạ độ \(Oxy\) và đánh dấu các điểm \(A\left( {3;\dfrac{{ - 1}}{2}} \right);B\left( { - 4;\dfrac{2}{4}} \right);C\left( {0;2,5} \right).\)

Phương pháp giải

Biểu diễn điểm \(M(a;b)\) trên hệ trục tọa độ ta làm như sau:

- Từ \(x=a\) ta dựng đường thẳng vuông góc với \(Ox\).

- Từ \(y=b\) ta dựng đường thẳng vuông góc với \(Oy\)

Giao điểm của hai đường này là điểm \(M\).

Hướng dẫn giải

- Cách vẽ: 

+ Đánh dấu điểm \(A\): 

• Từ \(x=3\) vẽ đường vuông góc với \(Ox\); từ \(y=- \dfrac{1}{2}\) vẽ đường vuông góc với \(Oy\).
• Giao điểm hai đường này là điểm \(A\).

+ Đánh dấu điểm \(B\):

• Từ \(x=-4\) vẽ đường vuông góc với \(Ox\); từ \(y= \dfrac{2}{4}\) vẽ đường vuông góc với \(Oy\).
• Giao điểm hai đường này là điểm \(B\).

+ Đánh dấu điểm \(C\):

• Từ \(x=0\) vẽ đường vuông góc với \(Ox\); từ \(y=2,5\) vẽ đường vuông góc với \(Oy\).
• Giao điểm hai đường này là điểm \(C\).

Hoặc điểm \(C\) là điểm biểu diễn số \(2,5\) trên trục tung \(Oy\).

a) Một điểm bất kì trên trục hoành có tung độ bằng bao nhiêu?

b) Một điểm bất kì trên trục tung có hoành độ bằng bao nhiêu?

Phương pháp giải

Muốn tìm tọa độ của một điểm bất kì trong mặt phẳng tọa độ, từ điểm đó ta vẽ các đường vuông góc với các trục tọa độ. Tọa độ giao điểm của các đường vuông góc này với các trục tọa độ cho ta biết tọa độ phải tìm.

Hướng dẫn giải

Câu a: Điểm trên trục hoành có tung độ bằng \(0\). 

Giải thích:

- Tìm tung độ của một điểm bất kì trên trục hoành như sau: 

- Từ điểm đó đến trục hoành ta vẽ đường vuông góc với trục tung. Đường này chính là trục hoành \(Ox\) và cắt \(Oy\) tại \(O\). Vậy điểm trên trục hoành có tung độ bằng \(0\).

Câu b: Điểm trên trục tung có hoành độ bằng \(0\).

Giải thích:

- Tìm hoành độ của một điểm bất kì trên trục tung như sau: 

- Từ điểm đó đến trục tung ta vẽ đường vuông góc với trục hoành. Đường này chính là trục tung \(Oy\) và cắt \(Ox\) tại \(O\). Vậy điểm trên trục tung có hoành độ bằng \(0\).

Tìm tọa độ các đỉnh của hình chữ nhật \(ABCD\) và của hình tam giác \(PQR\) trong hình \(20.\) 

Phương pháp giải

Từ điểm cần xác định tọa độ ta vẽ các đường vuông góc với các trục tọa độ, xác định giao điểm của các đường này với các trục tọa độ từ đó ta tìm được tọa độ của điểm cần xác định.

Hướng dẫn giải

- Từ các đỉnh của hình chữ nhật \(ABCD\) và các đỉnh của hình tam giác \(PQR\) ta vẽ các đường vuông góc xuống các trục \(Ox\) và \(Oy\).

- Tọa độ giao điểm của các đường vuông góc với \(Ox\) và \(Oy\) cho ta biết hoành độ và tung độ của điểm đó. Vậy tọa độ các đỉnh của hình chữ nhật \(ABCD\) là 

\(A (0,5; 2)\); \(B (2;2)\); \(C (2;0)\); \(D (0,5; 0)\).

- Tọa độ các đỉnh của hình \(\Delta PQR\) là:

\(P (-3;3)\); \(Q (-1;1)\); \(R(-3;1)\).

Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(A(-4; -1); B(-2; -1), C(-2; -3);\) \( D(-4; -3).\) Tứ giác \(ABCD\) là hình gì?

Phương pháp giải

Cách biểu diễn \(M(a; b)\) trên hệ trục tọa độ: Từ hoành độ \(x=a\) ta vẽ đường vuông góc với \(Ox\) và từ tung độ \(y=b\) ta vẽ đường vuông góc với \(Oy\). Giao điểm hai đường vuông góc này là điểm \(M\).

Hướng dẫn giải

Vẽ một hệ trục tọa độ \(Oxy\) (hình vẽ) và đánh dấu các điểm như sau: 

- Từ tọa độ của các điểm ta vẽ các đường vuông góc với các trục \(Ox,Oy\), giao điểm của các đường vuông góc là vị trí các điểm cần đánh dấu.

- Đánh dấu điểm \(A(-4; -1)\): Từ hoành độ \(x=-4\) ta vẽ đường vuông góc với \(Ox\) và từ tung độ \(y=-1\) ta vẽ đường vuông góc với \(Oy\). Giao điểm hai đường vuông góc này là điểm \(A\).

- Tương tự như thế ta đánh dấu các điểm \(B,C,D.\)

- Theo hình vẽ tứ giác \(ABCD\) là hình vuông vì có \(4\) cạnh bằng nhau và \(4\) góc vuông.

Hàm số \(y\) được cho trong bảng sau:

a) Viết tất cả các cặp giá trị tương ứng \((x;y)\) của hàm số trên.

b) Vẽ một hệ trục tọa độ \(Oxy\) và xác định các điểm biểu diễn các cặp giá trị tương ứng của \(x\) và \(y\) ở câu a.

Phương pháp giải

a) Để viết tất cả các cặp giá trị tương ứng \((x;y)\) ta liệt kê các cặp giá trị theo từng cột được cho trong bảng giá trị.

b) Cách biểu diễn \(M(a; b)\) trên hệ trục tọa độ.

Từ hoành độ \(x=a\) ta vẽ đường vuông góc với \(Ox\) và từ tung độ \(y=b\) ta vẽ đường vuông góc với \(Oy\). Giao điểm hai đường vuông góc này là điểm \(M\).

Hướng dẫn giải

Câu a: Tất cả các cặp giá trị tương ứng \((x;y)\) là: \((0;0); (1;2); (2; 4); (3; 6);\)\(\, (4; 8).\)

Câu b: Gọi \(O(0;0), A(1;2); B(2; 4); C(3; 6);\)\(\, D(4; 8).\)

Vẽ một hệ trục tọa độ \(Oxy\) và xác định các điểm biểu diễn các cặp giá trị tương ứng của \(x\) và \(y\) ở câu a.

- Xác định điểm có cặp giá trị \((0;0)\) chính là gốc tọa độ \(O\)

- Xác định điểm có cặp giá trị \((1;2)\): Từ hoành độ \(x=1\) ta vẽ đường vuông góc với \(Ox\) và từ tung độ \(y=2\) ta vẽ đường vuông góc với \(Oy\). Giao hai đường vuông góc vừa vẽ là điểm cần tìm và kí hiệu là \(A(1;2)\).

- Tương tự ta xác định các điểm biểu diễn các cặp giá trị tương ứng của \(x\) và \(y\) còn lại.

Chiều cao và tuổi của bốn bạn Hồng, Hoa, Đào, Liên được biểu diễn trên mặt phẳng tọa độ (h.21). Hãy cho biết:

a) Ai là người cao nhất và cao bao nhiêu?

b) Ai là người ít tuổi nhất và bao nhiêu tuổi?

c) Hồng và Liên ai cao hơn và ai nhiều tuổi hơn?

Phương pháp giải

Muốn tìm tọa độ của một điểm bất kì trong mặt phẳng tọa độ, từ điểm đó ta vẽ các đường vuông góc với các trục tọa độ. Giao điểm của các đường vuông góc này với các trục \(Ox\) và \(Oy\) cho ta biết hoành độ và tung độ của điểm đó.

Hướng dẫn giải

- Từ điểm biểu diễn của bạn Đào ta vẽ các đường vuông góc với trục tuổi và trục chiều cao, ta có hoành độ và tung độ tương ứng với điểm biểu diễn là \(14\) và \(15\).

- Suy ra bạn Đào là \(14\) tuổi và cao \(15\) dm.

- Tương tự ta có: 

• Hồng cao \(14\) dm, Hoa cao \(14\) dm và Liên cao \(13\) dm.
• Liên \(14\) tuổi, Hoa \(13\) tuổi và Hồng \(11\) tuổi.

a) Đào là người cao nhất và cao \(15\) dm.

b) Hồng là người ít tuổi nhất là \(11\) tuổi.

c) Hồng cao hơn Liên \(1\) dm và Liên nhiều tuổi hơn Hồng \(3\) tuổi.