Giải bài tập SGK Toán 7 Bài 2: Hai tam giác bằng nhau

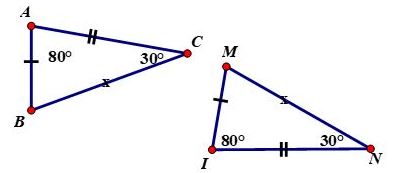
 Trong các hình 63, 64 các tam giác nào bằng nhau (Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.

Phương pháp giải:

Áp dụng định lí tổng ba góc trong một tam giác bằng \(180^0\)

Áp dụng định nghĩa hai tam giác bằng nhau.  

Hướng dẫn giải:

Hình 63 ta có: 

\(\widehat{A}=\widehat{I}=80^0\),

\(\widehat{C}=\widehat{N}=30^0\)

\(\widehat{B}=\widehat{M}=180^0-(80^0+30^0)=70^0\)

\(AB=IM, AC=IN, BC=MN\).

Suy ra \(∆ABC=∆IMN\)

Hình 64 ta có:

\(\widehat {RQH} = \widehat {QRP} = {80^0}\)

Áp dụng định lí tổng các góc của một tam giác vào \(\Delta QHR\) ta có:

\(\eqalign{
& \widehat {QHR} + \widehat {HRQ} + \widehat {RQH} = {180^o} \cr
& \Rightarrow \widehat {HRQ} = {180^o} - \left( {\widehat {QHR} + \widehat {RQH}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\; = {180^o} - \left( {{{40}^o} + {{80}^o}} \right) = {60^o} \cr} \)

\(\Rightarrow \widehat {HRQ} = \widehat {PQR} = {60^o}\)

Áp dụng định lí tổng các góc của một tam giác vào \(\Delta PQR\) ta có:

\(\eqalign{
& \widehat {PQR} + \widehat {QRP} + \widehat {RPQ} = {180^o} \cr
& \Rightarrow \widehat {RPQ} = {180^o} - \left( {\widehat {PQR} + \widehat {QRP}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} - \left( {{{60}^o} + {{80}^o}} \right) = {40^o} \cr} \)

\( \Rightarrow \widehat {RPQ} = \widehat {QHR} = {40^o}\)

\(QH= RP, HR= PQ, QR=RQ\).

Suy ra \(∆HQR=∆PRQ\). 

 Cho \(∆ ABC= ∆ HIK\)

a) Tìm cạnh tương ứng với cạnh \(BC\). Tìm góc tương ứng với góc \(H\)

b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.

Phương pháp giải:

Áp dụng định nghĩa hai tam giác bằng nhau. 

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Hướng dẫn giải:

Câu a: Ta có \(∆ ABC= ∆ HIK\), nên cạnh tương ứng với \(BC\) là cạnh \(IK\), góc tương ứng với góc \(H\) là góc \(A\).

Câu b: \(∆ ABC= ∆ HIK\)  

Suy ra: \(AB=HI, AC=HK, BC=IK\).

\(\widehat{A}=\widehat{H}\), \(\widehat{B}=\widehat{ I  }\),\(\widehat{C}=\widehat{K}\).

Cho \(∆ ABC= ∆HIK\) trong đó cạnh \(AB = 2cm\),\(\widehat{B}=40^0\), \(BC= 4cm\). Em có thể suy ra số đo của những cạnh nào, những góc nào của tam giác \(HIK\)?

Phương pháp giải:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Hướng dẫn giải:

\(∆ ABC= ∆HIK\) nên suy ra các cạnh tương ứng bằng nhau \(HI=AB=2cm\), \(IK=BC=4cm\).

Các góc tương ứng bằng nhau: \(\widehat{I}=\widehat{B}=40^0\). 

Cho \(∆ABC= ∆ DEF.\) Tính chu vi mỗi tam giác nói trên biết \(AB=4cm, BC=6cm, DF= 5cm\) (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó)

Phương pháp giải:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác. 

Hướng dẫn giải:

Ta có \(∆ABC= ∆ DEF\) 

Suy ra: \(AB=DE=4cm,\) \(BC=EF=6cm,\) \(DF=AC=5cm.\)

Chu vi của tam giác \(ABC\) là: \(AB+BC+AC = 4+6+5=15 \;(cm)\)

Chu vi của tam giác \(DEF\) là: \(DE+EF+DF = 4+6+5=15\; (cm )\) 

Cho hai tam giác bằng nhau: Tam giác \(ABC\) (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một tam giác có ba đỉnh \(H,I,K.\) Viết kí hiệu về sự bằng nhau của hai tam giác đó biết:

\(AB=KI\), \(\widehat{B}=\widehat{K}\)

Phương pháp giải:

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Hướng dẫn giải:

Ta có \(\widehat{B}=\widehat{K}\) nên \(B, K\) là hai đỉnh tương ứng.

\(AB= KI\) nên \(A, I\) là hai đỉnh tương ứng.

Do đó \(C,\,H\) là hai đỉnh tương ứng.

Vậy \(∆ABC=∆IKH\).