Giải bài tập SGK Toán 7 Ôn tập Chương 4: Biểu thức đại số
Hướng dẫn Giải bài tập SGK Toán 7 Bài Biểu thức đại số sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 57 trang 49 SGK Toán 7
Viết một biểu thức đại số của hai biến \(x, y\) thỏa mãn từng điều kiện sau:
a) Biểu thức đó là đơn thức.
b) Biểu thức đó là đa thức mà không phải là đơn thức.
Phương pháp giải
- Dựa vào định nghĩa:
- Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
- Đa thức là một tổng của những đơn thức.
Chú ý: Mỗi đơn thức là một đa thức nhưng một đa thức chưa chắc đã là đơn thức.
Hướng dẫn giải
Câu a: Biểu thức đại số của hai biến \(x; y\) là đơn thức: \(2{x^2}{y^3}\)
Câu b: Biểu thức đại số của hai biến \(x; y\) là đa thức mà không phải đơn thức: \(2x + 5y\).
2. Giải bài 58 trang 49 SGK Toán 7
Tính giá trị mỗi biểu thức sau tại \(x = 1; y = -1\) và \(z =- 2\).
a) \(2xy(5{x^2}y + 3x-z)\)
b) \(x{y^2} + {y^2}{z^3} + {z^3}{x^4}\).
Phương pháp giải
Thay giá trị tương ứng của \(x\), \(y\) và \(z\) vào biểu thức rồi tính giá trị của biểu thức đó.
Hướng dẫn giải
Câu a:
Thay \(x = 1; y = -1; z = -2\) vào biểu thức ta được:
\(\eqalign{
& 2xy(5{x^2}y + 3x - z) \cr
& = 2.1.\left( { - 1} \right).[{5.1^2}.\left( { - 1} \right) + 3.1 - \left( { - 2} \right)] \cr
& = - 2.\left( { - 5 + 3 + 2} \right) \cr
& = - 2.0 = 0 \cr} \)
Vậy đa thức có giá trị bằng \(0\) tại \(x = 1, y =-1, z = -2\)
Câu b:
Thay \(x = 1; y = -1; z = -2\) vào biểu thức ta được:
\(\eqalign{
& x{y^2} + {y^2}{z^3} + {z^3}{x^4} \cr
& = 1.{\left( { - 1} \right)^2} + {\left( { - 1} \right)^2}.{\left( { - 2} \right)^3} + {\left( { - 2} \right)^3}{.1^4} \cr
& = 1 + \left( { - 8} \right) + \left( { - 8} \right) = - 15 \cr} \)
Vậy đa thức có giá trị bằng \(-15\) tại \(x = 1, y = -1, z = -2\).
3. Giải bài 59 trang 49 SGK Toán 7
Hãy điền đơn thức thích hợp vào mỗi ô trống dưới đây:
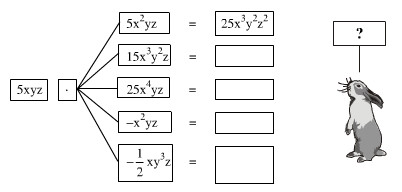
Phương pháp giải
Áp dụng quy tắc nhân đơn thức với đơn thức: Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.
Hướng dẫn giải
\(5xyz.15{x^3}{y^2}z \)\(\,= \left( {5.15} \right){\rm{.}}\left( {x.{x^3}} \right){\rm{.}}\left( {y.{y^2}} \right){\rm{.}}\left( {z.z} \right){\rm{ }} \)
\(\,= 75{x^4}{y^3}{z^2}\)
\(5xyz.25{x^4}yz \)\(\,= \left( {5.25} \right).\left( {x.{x^4}} \right).\left( {y.y} \right).\left( {z.z} \right) \)
\(\,= 125{x^5}{y^2}{z^2}\)
\(5xyz.\left( { - {x^2}yz} \right) \)\(\,= \left[ {5.\left( { - 1} \right)} \right].\left( {x.{x^2}} \right).\left( {y.y} \right).\left( {z.z} \right) \)
\(\,= - 5{x^3}{y^2}{z^2}\)
\(5xyz.\left( { - \dfrac{1}{2}x{y^3}z} \right) \)
\(\,= \left[ {5.\left( { - \dfrac{1}{2}} \right)} \right].\left( {x.x} \right).\left( {y.{y^3}} \right).\left( {z.z} \right) \)
\(\,= - \dfrac{5}{2}{x^2}{y^4}{z^2}\)
4. Giải bài 60 trang 49 SGK Toán 7
Có hai vòi nước: vòi thứ nhất chảy vào bể \(A\), vòi thứ hai chảy vào bể \(B\). Bể \(A\) đã có sẵn \(100\) lít nước. Bể \(B\) chưa có nước. Mỗi phút vòi thứ nhất chảy được \(30\) lít, vòi thứ hai chảy được \(40\) lít.
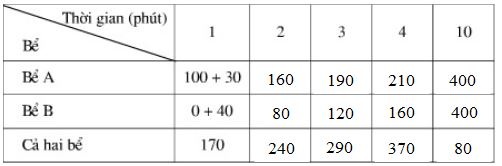
a) Tính lượng nước có trong mỗi bể sau thời gian \(1, 2, 3, 4, 10\) phút rồi điền kết quả vào bảng sau (giả thiết bể đủ lớn để chứa nước):
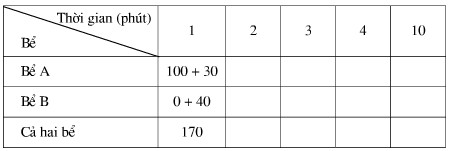
b) Viết biểu thức đại số biểu thị số lít nước trong mỗi bể sau thời gian \(x\) phút.
Phương pháp giải
- Để tính được số nước ở bể A: ta tính số nước mà vòi A chảy được vào bể sau số phút tương ứng rồi cộng với \(100\).
- Để tính được số nước ở bể B: ta tính số nước mà vòi B chảy được vào bể sau số phút tương ứng.
Hướng dẫn giải
Câu a:
Sau \(1\) phút bể \(A\) có \(100 + 30 = 130\) (lít), bể B có \(40\) (lít)
\( \Rightarrow \) Cả \(2\) bể có \(130+40=170\) (lít)
Sau \(2\) phút bể \(A\) có \(100 + 2.30 = 160\) (lít), bể B có \(40.2 = 80\) (lít)
\( \Rightarrow \) Cả \(2\) bể có \(160+80=240\) (lít)
Sau \(3\) phút bể \(A\) có \(100 + 3.30 = 190\) (lít), bể \(B\) có \(40.3 = 120\) (lít)
\( \Rightarrow \) Cả \(2\) bể có \(190+120=310\) (lít)
Sau \(4\) phút bể \(A\) có \(100 + 4.30 = 220\) (lít), bể \(B\) có \(40.4 = 160\) (lít)
\( \Rightarrow \) Cả \(2\) bể có \(220+160=380\) (lít)
Sau \(10\) phút bể \(A\) có \(100 + 10.30 = 400\) (lít), bể \(B\) có \(40.10 = 400\) (lít)
\( \Rightarrow \) Cả \(2\) bể có \(400+400=800\) (lít)
Kết quả được điền vào bảng sau:
Câu b:
Số lít nước trong bể \(A\) sau thời gian \(x\) phút là \(100 +30x\) (lít)
Số lít nước trong bể \(B\) sau thời gian \(x\) phút \(40x\) (lít).
5. Giải bài 61 trang 50 SGK Toán 7
Tính tích các đơn thức sau rồi tìm hệ số và bậc của tích tìm được.
a) \(\dfrac{1}{4}x{y^3}\) và \(- 2{x^2}y{z^2}\)
b) \( - 2{x^2}yz\) và \( - 3x{y^3}z\)
Phương pháp giải
- Áp dụng qui tắc nhân đơn thức với đơn thức.
- Bậc của đơn thức là tổng số mũ của các biến trong đơn thức đó.
Hướng dẫn giải
Câu a:
Tích của \(\dfrac{1}{4}x{y^3}\) và \(- 2{x^2}y{z^2}\) là:
\(\dfrac{1}{4}x{y^3}.\left( { - 2{x^2}y{z^2}} \right)\)\(\, = \left[ {\dfrac{1}{4}.\left( { - 2} \right)} \right].\left( {x.{x^2}} \right).\left( {{y^3}.y} \right).{z^2} \)\(\,= \dfrac{{ - 1}}{2}{x^3}{y^4}{z^2}\)
Đơn thức tích có hệ số là \(\dfrac{{ - 1}}{2}\) ; có bậc là \(3+4+2=9\).
Câu b:
Tích của \( - 2{x^2}yz\) và \( - 3x{y^3}z\) là:
\( - 2{x^2}yz.\left( { - 3x{y^3}z} \right) \)
\(\,= \left[ {\left( { - 2} \right).\left( { - 3} \right)} \right].\left( {{x^2}.x} \right)\left( {y.{y^3}} \right)\left( {z.z} \right)\)
\(\, = 6{x^3}{y^4}{z^2}\)
Đơn thức tích có hệ số là \(6\); có bậc \(3+4+2=9\).
6. Giải bài 62 trang 50 SGK Toán 7
Cho hai đa thức:
\(P\left( x \right) = {x^5} - 3{x^2} + 7{x^4} - 9{x^3} + {x^2} \)\(- \dfrac{1}{4}x\)
\(Q\left( x \right) = 5{x^4} - {x^5} + {x^2} - 2{x^3} + 3{x^2}\)\( - \dfrac{1}{4}\)
a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
b) Tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).
c) Chứng tỏ rằng \(x = 0\) là nghiệm của đa thức \(P(x)\) nhưng không phải là nghiệm của đa thức \(Q(x)\).
Phương pháp giải
- Thu gọn và sắp xếp mỗi đa thức trên theo lũy thừa giảm của biến.
- Áp dụng qui tắc cộng, trừ đa thức một biến.
- Muốn kiểm tra một số \(a\) có phải là nghiệm của đa thức \(f(x)\) không ta làm như sau:
- Tính \(f(a)=?\) ( giá trị của \(f(x)\) tại \(x = a\))
- Nếu \(f(a)= 0 \) \(\Rightarrow\) \( a\) là nghiệm của \(f(x)\)
- Nếu \(f(a)≠0\) \( \Rightarrow \) \(a\) không phải là nghiệm của \(f(x)\).
Hướng dẫn giải
Câu a:
Ta có:
\(P\left( x \right) = {x^5} - 3{x^2} + 7{x^4} - 9{x^3} + {x^2} \)\(- \dfrac{1}{4}x\)
\( = {x^5} + 7{x^4} - 9{x^3} + \left( { - 3{x^2} + {x^2}} \right) \)\(\,- \dfrac{1}{4}x\)
\( = {x^5} + 7{x^4} - 9{x^3} - 2{x^2} - \dfrac{1}{4}x\)
\(Q\left( x \right) = 5{x^4} - {x^5} + {x^2} - 2{x^3} + 3{x^2}\)\( - \dfrac{1}{4}\)
\( = - {x^5} + 5{x^4} - 2{x^3} + \left( {{x^2} + 3{x^2}} \right) - \dfrac{1}{4}\)
\( = - {x^5} + 5{x^4} - 2{x^3} + 4{x^2} - \dfrac{1}{4}\)
Câu b:
Câu c:
Ta có:
\( P(x)= {x^5} + 7{x^4} - 9{x^3} - 2{x^2} - \dfrac{1}{4}x\)
Nên \(P\left( 0 \right) = {0^5} + {7.0^4} - {9.0^3} - {2.0^2} - \dfrac{1}{4}.0\)\(\,=0\)
\( \Rightarrow x = 0\) là nghiệm của \(P(x)\).
Ta có: \( Q(x) = - {x^5} + 5{x^4} - 2{x^3} + 4{x^2} - \dfrac{1}{4}\)
Nên \(Q\left( 0 \right) = - {0^5} + {5.0^4} - {2.0^3} + {4.0^2} - \dfrac{1}{4}\)\( = - \dfrac{1}{4} \ne 0\)
\( \Rightarrow x = 0\) không phải là nghiệm của \(Q(x)\).
7. Giải bài 63 trang 50 SGK Toán 7
Cho đa thức: \(M(x) = 5{{\rm{x}}^3} + 2{{\rm{x}}^4} - {x^2} + 3{{\rm{x}}^2} - {x^3}\)\( - {x^4} + 1 - 4{{\rm{x}}^3}\)
a) Sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Tính \(M(1)\) và \(M(-1)\)
c) Chứng tỏ rằng đa thức trên không có nghiệm.
Phương pháp giải
- Thu gọn đa thức \(M(x)\) sau đó sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
- Thay giá trị tương ứng của \(x\) vào đa thức sau khi đã rút gọn rồi tính giá trị của đa thức đó.
- Đa thức không có nghiệm khi và chỉ khi đa thức đó luôn khác \(0\) với mọi \(x\).
Hướng dẫn giải
Câu a: Rút gọn:
\(M(x) = 5x^3 + 2x^4 – x^2 + 3x^2 – x^3 – x^4 + 1 – 4x^3\)
\(= (2x^4 – x^4) + (5x^3 – x^3 – 4x^3) + (– x^2 + 3x^2) + 1\)
\(= x^4 + 0 + 2x^2 + 1\)
\(= x^4 + 2x^2 + 1.\)
Sắp xếp các hạng tử của đa thức \(M(x)\) theo lũy thừa giảm của biến:
\(M(x)={x^4} + 2{x^2} + 1\)
Câu b:
Ta có: \(M(x)={x^4} + 2{x^2} + 1\)
Nên:
\(M\left( 1 \right) = {1^4} + {2.1^2} + 1 = 4\)
\(M\left( { - 1} \right) = {\left( { - 1} \right)^4} + 2.{\left( { - 1} \right)^2} + 1 = 4\)
Câu c:
Ta có: \(M\left( x \right) = {x^4} + 2{x^2} + 1\)
Vì \({x^4} \ge 0\) với mọi \(x\, \in\mathbb R\)
và \({x^2} \ge 0\) với mọi \(x\, \in\mathbb R\)
\(\;\Rightarrow {x^4} + 2{x^2} + 1 \ge 1> 0\) với mọi \(x\, \in\mathbb R\)
\(\Rightarrow M\left( x \right)\) không có nghiệm.
8. Giải bài 64 trang 50 SGK Toán 7
Hãy viết các đơn thức đồng dạng với đơn thức \({x^2}y\) sao cho tại \(x = -1\) và \(y = 1\), giá trị của các đơn thức đó là số tự nhiên nhỏ hơn \(10\).
Phương pháp giải
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác \(0\) và có cùng phần biến.
Hướng dẫn giải
Đơn thức đồng dạng với đơn thức \({x^2}y\) là: \(a{x^2}y\) với \(a\) là hằng số khác \(0\).
Tại \(x = -1\) và \(y = 1\) ta có: \(a{x^2}y\)\(=a.(-1)^2.1=a\)
Vì tại \(x = -1\) và \(y = 1\) giá trị của đơn thức là số tự nhiên nhỏ hơn \(10\) nên: \(a < 10\)
Vậy \(a\) là số tự nhiên (khác \(0\)) nhỏ hơn \(10\) nên \(a\) nhận các giá trị \(1;2;3;4;5; 6;7;8;9\).
Vậy các đơn thức thỏa mãn yêu cầu đề bài là: \({x^2}y;\,\,2{x^2}y;\,\,3{x^2}y;\,\,4{x^2}y;\,\,5{x^2}y;\)\(\,\,6{x^2}y;\,\,7{x^2}y;\,\,8{x^2}y;\,\,9{x^2}y\).
9. Giải bài 65 trang 51 SGK Toán 7
Trong các số cho bên phải mỗi đa thức, số nào là nghiệm của đa thức đó?
Phương pháp giải
Muốn kiểm tra một số \(a\) có phải là nghiệm của đa thức \(f(x)\) không ta làm như sau:
• Tính \(f(a)=?\) (giá trị của \(f(x)\) tại \(x = a\))
• Nếu \(f(a)= 0\) \( \Rightarrow a\) là nghiệm của \(f(x)\)
• Nếu \(f(a)≠0 \Rightarrow a\) không phải là nghiệm của \(f(x)\).
Hướng dẫn giải
Câu a:
Ta có: \(A(x) = 2x - 6\)
\(\eqalign{
& A\left( { - 3} \right) = 2.\left( { - 3} \right) - 6 = - 6 - 6 \cr&\;\;\;\;\;\;\;\;\;\;\;\;= - 12\ne 0 \cr
& A\left( 0 \right) = 2.0 - 6 = 0 - 6 = - 6 \ne 0\cr
& A\left( 3 \right) = 2.3 - 6 = 6 - 6 = 0 \cr} \)
Vậy \(A(x) = 2x - 6\) có nghiệm là \(3\)
Câu b:
Ta có: \(B(x) = 3x + \dfrac{1}{2}\)
\(\eqalign{
& B\left( {{{ - 1} \over 6}} \right) = 3.\left( {{{ - 1} \over 6}} \right) + {1 \over 2} = {{ - 3} \over 6} + {1 \over 2}\cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= {{ - 1} \over 2} + {1 \over 2} = 0 \cr
& B\left( {{{ - 1} \over 3}} \right) = 3.\left( {{{ - 1} \over 3}} \right) + {1 \over 2} = {{ - 3} \over 3} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= - 1 + {1 \over 2} = {{ - 2} \over 2} + {1 \over 2} = {{ - 1} \over 2} \ne 0\cr
& B\left( {{1 \over 6}} \right) = 3.{1 \over 6} + {1 \over 2} = {3 \over 6} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\; = {1 \over 2} + {1 \over 2} = 1\ne 0 \cr
& B\left( {{1 \over 3}} \right) = 3.{1 \over 3} + {1 \over 2} = {3 \over 3} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\; = 1 + {1 \over 2} = {2 \over 2} + {1 \over 2} = {3 \over 2} \ne 0\cr} \)
\(B(x) = 3x + \dfrac{1}{2}\) có nghiệm là \( - \dfrac{1}{6}\)
Câu c:
Ta có: \(M\left( x \right) = {x^2}-3x + 2\)
\(\eqalign{
& M\left( { - 2} \right) = {\left( { - 2} \right)^2} - 3.\left( { - 2} \right) + 2 = 4 + 6 + 2 = 12 \cr
& M\left( { - 1} \right) = {\left( { - 1} \right)^2} - 3.\left( { - 1} \right) + 2 = 1 + 3 + 2 = 6 \cr
& M\left( 1 \right) = {1^2} - 3.1 + 2 = 1 - 3 + 2 = 0 \cr
& M\left( 2 \right) = {2^2} - 3.2 + 2 = 4 - 6 + 2 = 0 \cr} \)
\(M\left( x \right) = {x^2}-3x + 2\) có nghiệm là \(1\) và \(2\).
Câu d:
Ta có: \(P\left( x \right) = {x^2} + 5x - 6\)
\(\eqalign{
& P\left( { - 6} \right) = {\left( { - 6} \right)^2} + 5.\left( { - 6} \right) - 6 = 36 - 30 - 6 = 0 \cr
& P\left( { - 1} \right) = {\left( { - 1} \right)^2} + 5.\left( { - 1} \right) - 6 = 1 - 5 - 6 = - 10 \cr
& P\left( 1 \right) = {1^2} + 5.1 - 6 = 1 + 5 - 6 = 0 \cr
& P\left( 6 \right) = {6^2} + 5.6 - 6 = 36 + 30 - 6 = 60 \cr} \)
\(P\left( x \right) = {x^2} + 5x - 6\) có nghiệm là \(1\) và \(-6\).
Câu e:
Ta có: \(Q\left( x \right) = {x^2} + x\)
\(\eqalign{
& Q\left( { - 1} \right) = {\left( { - 1} \right)^2} + \left( { - 1} \right) = 1 + \left( { - 1} \right) = 0 \cr
& Q\left( 0 \right) = {0^2} + 0 = 0 \cr
& Q\left( {{1 \over 2}} \right) = {\left( {{1 \over 2}} \right)^2} + {1 \over 2} = {1 \over 4} + {1 \over 2} = {3 \over 4} \cr
& Q\left( 1 \right) = {1^2} + 1 = 1 + 1 = 2 \cr} \)
\(Q\left( x \right) = {x^2} + x\) có nghiệm là \(-1\) và \(0\).
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Khái niệm về biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 2: Giá trị của một biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 3: Đơn thức
- doc Giải bài tập SGK Toán 7 Bài 4: Đơn thức đồng dạng
- doc Giải bài tập SGK Toán 7 Bài 5: Đa thức
- doc Giải bài tập SGK Toán 7 Bài 6: Cộng, trừ đa thức
- doc Giải bài tập SGK Toán 7 Bài 7: Đa thức một biến
- doc Giải bài tập SGK Toán 7 Bài 8: Cộng, trừ đa thức một biến
- doc Giải bài tập SGK Toán 7 Bài 9: Nghiệm của đa thức một biến
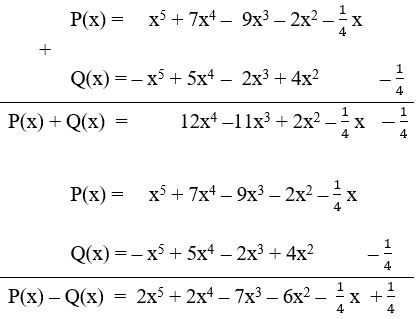
.JPG)
