Giải bài tập SGK Toán 7 Bài 2: Giá trị của một biểu thức đại số

Đố: Giải thưởng toán học Việt Nam (dành cho giáo viên và học sinh phổ thông) mang tên nhà toán học nổi tiếng nào ?

(Quê ông ở Hà Tĩnh. Ông là người thầy của nhiều thế hệ các nhà toán học nước ta trong thế kỉ \(XX\)).

Hãy tính giá trị của các biểu thức sau tại \(x = 3, y = 4\) và \(z = 5\) rồi viết các chữ tương ứng với các số tìm được vào các ô trống dưới đây, em sẽ trả lời được câu hỏi trên:

N: \({x^2}\);                             

Ê: \(2{z^2} + 1\);

T: \({y^2}\) ;                           

H: \({x^2} + {y^2}\)

Ă: \(\dfrac{1}{2}(xy + z)\);              

V: \({z^2}-1\);

L: \({x^2} - {y^2}\)                                     

I: Biểu thức biểu thị chu vi của hình chữ nhật có các cạnh là \(y, z\).

M: Biểu thức biểu thị cạnh huyền của tam giác vuông có hai cạnh góc vuông \(x, y\).

Hướng dẫn giải

Lần lượt tính giá trị biểu thức tại \(x = 3, y = 4, z = 5\) ta được 

N:   \({x^2} = {3^2} = 9\); 

T:   \({y^2} = {4^2} = 16\); 

Ă:   \(\dfrac{1}{2}(xy + z) = \dfrac{1}{2}(3.4 +5)= 8,5\);   

L:   \({x^2} - {y^2} = {3^2} - {4^2} = 9 - 16 =  - 7\);

M:   Gọi \(t\) là độ dài cạnh huyền của tam giác vuông có hai cạnh góc vuông là \(x,y\)

Áp dụng định lí Pitago ta có:

\({t^2} = {x^2} + {y^2} = {3^2} + {4^2} = 25\)

\( \Rightarrow t = 5\)

Ê:  \(2{z^2} + 1 = {2.5^2} + 1 = 50 + 1 = 51\);

H:  \({x^2} + {y^2} = {3^2} + {4^2} = 25\);

V:   \({z^2}-1 = {5^2}-1 = 24\);

I:  Chu vi của hình chữ nhật có các cạnh là \(y, z\) là: \(2\left( {y + z} \right) = 2\left( {4 + 5} \right) = 18\);

 Điền vào ô trống:

Vậy giải thưởng toán học Việt Nam mang tên nhà toán học nổi tiếng Lê Văn Thiêm.

Tính giá trị các biểu thức sau tại  \(m = -1\) và \(n = 2\):

a) \(3m - 2n\);

b) \(7m + 2n - 6\).

Hướng dẫn giải

Câu a:

Thay \(m = -1\) và \(n = 2\) vào biểu thức \(3m - 2n\) ta có:

\(3.(-1) - 2.2 = -3 - 4 = -7\)

Vậy giá trị của biểu thức \(3m - 2n\) tại \(m = -1\) và \(n = 2\) là \(-7\).

Câu b:

Thay \(m = -1\) và \(n = 2\) vào biểu thức  \(7m + 2n - 6\) ta có

\(7.(-1) + 2.2 - 6 = -7 + 4 - 6 = -9\)

Vậy giá trị của biểu thức \(7m + 2n - 6\) tại \(m = -1\) và \(n = 2\) là \(- 9\).

Đố: Ước tính số gạch cần mua ? Giả sử gia đình em cần lát một nền nhà hình chữ nhật bằng gạch hình vuông có cạnh là \(30\) cm.

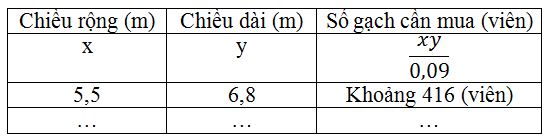
Hãy đo kích thước nền nhà đó rồi ghi vào ô trống trong bảng sau:

Hướng dẫn giải

Học sinh tự làm (như bài thực hành, bằng cách đo chiều dài, chiều rộng của lớp học, thư viện, hội trường, phòng bộ môn… rồi tính theo công thức rồi điền vào bảng). 

Trước hết, các bạn cần hiểu xem cột 3 (số gạch cần mua) được tính như thế nào.

Đổi: \(30\;cm = 0,3\; m\)

- Diện tích của nền nhà hình chữ nhật bằng \(x.y (m^2)\).

- Diện tích của viên gạch hình vuông bằng \(0,3^2 = 0,09 (m^2)\).

\( \Rightarrow\) Số gạch cần mua bằng diện tích nền nhà chia cho diện tích 1 viên gạch: \((x . y) : 0,09\) viên hay bằng \( \dfrac{xy}{0,09}\) viên

Sau đó, đo nền nhà của bạn.

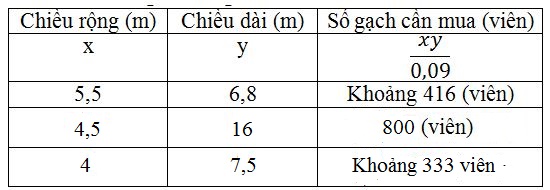
Dưới đây là 2 số liệu ví dụ:

VD1: Chiều rộng \(x = 4,5m\); chiều dài \(y = 16m\)

Số viên gạch cần mua là: \(\dfrac{{4,5.16}}{{0,09}} = 800\) (viên)

VD2: Chiều rộng \(x = 4m\); chiều dài \(y = 7,5m\)

Số viên gạch cần mua là: \(\dfrac{{4.7,5}}{{0,09}} \approx 333\) (viên)

Ta điền được vào bảng như sau:

Tính giá trị của biểu thức \({x^2}{y^3} + xy\) tại \(x = 1\) và \(y = \dfrac{1}{2}\).

Hướng dẫn giải

Thay \(x = 1\) và \(y = \dfrac{1}{2}\) vào biểu thức \({x^2}{y^3} + xy,\) ta có:

\({1^2}.{\left( {\dfrac{1}{2}} \right)^3} + 1.\dfrac{1}{2} = 1.\dfrac{1}{8} + \dfrac{1}{2}\)\(\, = \dfrac{1}{8} + \dfrac{1}{2} = \dfrac{1}{8} + \dfrac{4}{8} = \dfrac{5}{8}\)

Vậy giá trị của biểu thức \({x^2}{y^3} + xy\) tại \(x = 1\) và \(y = \dfrac{1}{2}\) là \(\dfrac{5}{8}\).