Giải bài tập SGK Toán 7 Bài 1: Tập hợp Q các số hữu tỉ

Điền kí hiệu ($∈, ∉, ⊂$) thích hợp vào ô vuông  

- 3 N ;                        -3  Z;                    -3  Q

   Z;                        Q;               N  Z  Q

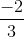
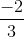
Phương pháp giải

• Tập hợp số tự nhiên: $\mathbb N = \left\{ {0;\;1;\;2;\;3.........} \right\}.$
• Tập hợp số nguyên: $\mathbb Z = \left\{ {...; - 3;\; - 2;\; - 1;\;0;\;1;\;2;\;3...} \right\}.$
• Tập hợp $\mathbb Q$ là tập hợp các số hữu tỉ gồm các số được viết dưới dạng phân số $\dfrac{a}{b}$ với $a, \, \, b \in\mathbb Z, \, \, b \neq 0.$

Hướng dẫn giải

 $- 3 \notin N$                   $- 3 \notin Z$                          $- 3 \in Q$

$- \frac{2}{3} \notin Z$                  $- \frac{3}{2} \in Q$                        $N \subset {\rm{Z}} \subset Q$

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\dfrac{3}{-4}$: $\dfrac{-12}{15} ; \dfrac{-15}{20}; \dfrac{24}{-32}; \dfrac{-20}{28}; \dfrac{-27}{36}$       

b) Biễu diễn số hữu tỉ $\dfrac{3}{-4}$ trên trục số.

Phương pháp giải

Rút gọn các phân số đã cho sau đó so sánh phân số rút gọn với $\dfrac{3}{-4}$

Hướng dẫn giải

Câu a: Ta có

$\dfrac{24}{-32} = \dfrac{24:8}{-32:8} = \dfrac{3}{-4}$

$\dfrac{-15}{20} = \dfrac{-15:(-5)}{20:(-5)} = \dfrac{3}{-4}$                   

$\dfrac{-27}{36} = \dfrac{-27:(-9)}{36:(-9)} = \dfrac{3}{-4}$ 

$\dfrac{{ - 12}}{{15}}=\dfrac{{ - 12:3}}{{15:3}}  = \dfrac{{ - 4}}{5} \ne \dfrac{3}{{ - 4}}$

$\dfrac{{ - 20}}{{28}}=\dfrac{{ - 20:4}}{{28:4}} = \dfrac{{ - 5}}{7} \ne \dfrac{3}{{ - 4}}$

Vậy những phân số biểu diễn số hữu tỉ  $\dfrac{3}{-4}$ là : $\dfrac{-15}{20}; \dfrac{24}{-32}; \dfrac{-27}{36}$

Câu b: Biểu diễn trên trục số

Do $\dfrac{3}{-4}$ lớn hơn $-1$ nhưng nhỏ hơn $0$ nên khoảng biểu diễn sẽ trong khoảng từ $-1$ tới $0.$ Chia khoảng cách từ $0$ đến $-1$ làm $4$ phần bằng nhau. Lấy $3$ phần từ $0$ qua thì được vị trí $\dfrac{3}{-4}$.

So sánh các số hữu tỉ

a) $x = \dfrac{2}{-7}$  và $y = \dfrac{-3}{11}.$

b) $x = \dfrac{-213}{300}$  và  $y = \dfrac{18}{-25}.$

c) $x = -0,75$ và $y = \dfrac{-3}{4}.$

Phương pháp giải

Quy đồng mẫu dương các số hữu tỉ đã cho sau đó áp dụng quy tắc so sánh hai phân số cùng mẫu dương.

Hướng dẫn giải

Câu a: Ta có  

$\eqalign{ & x = {2 \over { - 7}} = {{ - 2} \over 7} = {{ - 2.11} \over {7.11}} = {{ - 22} \over {77}} \cr  & y = {{ - 3} \over {11}} = {{ - 3.7} \over {11.7}} = {{ - 21} \over {77}} \cr}$

Vì $-22 < -21$ và $77> 0$ nên $\dfrac{{ - 22}}{{77}} < \dfrac{{ - 21}}{{77}}$ hay  $\dfrac{2}{{ - 7}} < \dfrac{{ - 3}}{{11}}$ tức là \(x

Câu b: $y = \dfrac{18}{-25} = \dfrac{18.(-12)}{-25.(-12)} = \dfrac{-216}{300};$

$x = \dfrac{-213}{300}$

Vì $-216 < -213$ và $300 > 0$ nên $\dfrac{-216}{300}<\dfrac{-213}{300}$ hay $\dfrac{18}{-25}< \dfrac{-213}{300}$, tức là $y < x.$

Câu c: $x = -0,75 = \dfrac{-75}{100} = \dfrac{-3}{4}; y = \dfrac{-3}{4}$

Vậy $x=y.$

So sánh số hữu tỉ $\dfrac{a}{b}$ $\left( {a,\;b \in Z,\;b \ne 0} \right)$ với số 0 khi $a,\, b$ cùng dấu và khi $a,\, b$ khác dấu.

Phương pháp giải

Dựa vào tính chất của các số hữu tỉ âm và số hữu tỉ dương để so sánh.

Hướng dẫn giải

Với ${a,\;b \in Z,\;b \neq  0}$ ta có

Khi $a ,\, b$ cùng dấu thì $\dfrac{a}{b} > 0.$ 

Khi $a ,\, b$ khác dấu thì $\dfrac{a}{b} < 0.$ 

Tổng quát: Số hữu tỉ  $\dfrac{a}{b}$ $\left( {a,\;b \in\mathbb Z,\;b \neq  0} \right)$

Dương nếu $a ,\, b$ cùng dấu

Âm nếu $a ,\, b$ khác dấu

Bằng $0$ nếu $a = 0.$

Giả sử  $x = \dfrac{a}{m}$; $y = \dfrac{b}{m}$ $\left( {a,\, b, \, m \in Z,\;m> 0} \right)$ và $x < y.$ Hãy chứng tỏ rằng nếu chọn  $z =\dfrac{a + b}{2m}$ thì ta có $x < z < y.$

Phương pháp giải

Sử dụng tính chất: Nếu $a,\;b,\;c \in Z$ và \(a

Hướng dẫn giải

Theo đề bài ta có $x = \dfrac{a}{m}$; $y = \dfrac{b}{m}$ $\left( {a,\, b, \, m \in Z,\;m> 0} \right)$ 

Vì $x < y$ tức là $\dfrac{a}{m}<\dfrac{b}{m}$ nên ta suy ra $a < b.$

Quy đồng mẫu số các phân số ta được:

$x =\dfrac{2a}{2m}$,  $y =\dfrac{2b}{2m}$;$z = \dfrac{a + b}{2m}$

Vì $a < b \Rightarrow a + a < a +b \Rightarrow 2a < a + b.$

Do $2a< a +b$ nên $\dfrac{2a}{2m}<\dfrac{a + b}{2m}$ hay $x < z  \, \, \, \, (1)$

Vì $a < b \Rightarrow a + b < b + b \Rightarrow a + b < 2b.$

Do $a+b < 2b$ nên $\dfrac{a + b}{2m}< \dfrac{2b}{2m}$ hay $z < y \, \, \,   (2)$

Từ (1) và (2) ta suy ra \(x < z < y.\