Giải bài tập SGK Toán 7 Bài 2: Cộng, trừ số hữu tỉ
Phần hướng dẫn giải bài tập SGK Cộng, trừ số hữu tỉ sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 7 Tập một.
Mục lục nội dung

1. Giải bài 6 trang 10 SGK Toán 7 tập 1
Tính
a) \(\frac{-1}{21}+\frac{-1}{28}\).
b) \(\frac{-8}{18}-\frac{15}{27}\).
c) \(\frac{-5}{12}+0,75\).
d) \(3,5+(\frac{-2}{7})\).
Phương pháp giải
Áp dụng các công thức cộng, trừ hai số hữu tỉ: Với \(a,\;b,\;m \in Z,\;\;m > 0\) ta có:
\(\begin{array}{l}
\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}\\
\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}
\end{array}\)
Hướng dẫn giải
câu a
\(\eqalign{
& \,\,{{ - 1} \over {21}} + {{ - 1} \over {28}} \cr
& = {{( - 1).4} \over {21.4}} + {{( - 1).3} \over {28.3}} \cr
& = {{ - 4} \over {84}} + {{ - 3} \over {84}}= {{ - 4+(-3)} \over {84}} \cr
&= {{ - 7} \over {84}} = {{ - 7:7} \over {84:7}}\cr
&= {{ - 1} \over {12}} \cr} \)
Câu b
\(\eqalign{
& {{ - 8} \over {18}} - {{15} \over {27}} \cr
& = {{ - 8} \over {18}} + \left( { - {{15} \over {27}}} \right)\cr
& ={{ - 8} \over {18}} + {{-15:3} \over {27:3}} \cr
& = {{ - 4} \over 9} + {{ - 5} \over 9} = {{ - 4+(-5)} \over 9}\cr
& = {{ - 9} \over 9} = - 1 \cr} \)
Câu c
\(\eqalign{
& \,\,{{ - 5} \over {12}} + 0,75= {{ - 5} \over {12}} + {75\over 100} \cr
&= {{ - 5} \over {12}} + {3 \over 4} \cr
& \, = {{ - 5} \over {12}} + {9 \over {12}} = {{ - 5 + 9} \over {12}} \cr
& \, = {4 \over {12}} = {4:4 \over {12:4}} = {1 \over 3} \cr} \)
Câu d
\(\eqalign{
& \,\,3,5 - \left( { - {2 \over 7}} \right) = 3,5 + {2 \over 7} \cr
& = {{35} \over {10}} + {2 \over 7} = {7 \over 2} + {2 \over 7} = {{49} \over {14}} + {4 \over {14}} \cr
& = {{49 + 4} \over {14}} = {{53} \over {14}} = 3{{11} \over {14}} \cr} \)
2. Giải bài 7 trang 10 SGK Toán 7 tập 1
Ta có thể viết số hữu tỉ \(\frac{-5}{16}\) dưới các dạng sau đây:
a) \(\frac{-5}{16}\) là tổng của hai số hữu tỉ âm . Ví dụ \(\frac{-5}{16} = \frac{-1}{8} + \frac{-3}{16}\)
b) \(\frac{-5}{16}\) là hiệu của hai số hữu tỉ dương. Ví dụ: \(\frac{-5}{16} = 1 - \frac{21}{16}\)
Với mỗi câu, em hãy tìm thêm một ví dụ
Phương pháp giải
Áp dụng các công thức cộng, trừ hai số hữu tỉ: Với \(a,\;b,\;m \in\mathbb Z,\;\;m > 0\) ta có:
\(\begin{array}{l}
\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}\\
\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}
\end{array}\)
Hướng dẫn giải
Có nhiều đáp số cho mỗi câu chẳng hạn:
Câu a
\(\frac{-5}{16} = \frac{-1}{4} + \frac{-1}{16} = \frac{-2}{16} + \frac{-3}{16} = \frac{-5}{20} + \frac{-1}{16} = ...\).
Câu b
3. Giải bài 8 trang 10 SGK Toán 7 tập 1
Tính
a) \(\frac{3}{7}+\left ( \frac{-5}{2} \right )+\left ( \frac{-3}{5} \right )\).
b) \(\left ( \frac{-4}{3} \right )+\left ( \frac{-2}{5} \right )+\left (\frac{-3}{2} \right )\).
c) \(\frac{4}{5}-\left ( \frac{-2}{7} \right )-\frac{7}{10}\).
d) \(\frac{2}{3}-\left [ (\frac{-7}{4})-(\frac{1}{2}+\frac{3}{8}) \right ]\).
Phương pháp giải
Áp dụng các công thức cộng, trừ hai số hữu tỉ: Với \(a,\;b,\;m \in Z,\;\;m > 0\) ta có:
\(\begin{array}{l}
\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}\\
\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}
\end{array}\)
Hướng dẫn giải
Câu a
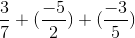 =
= 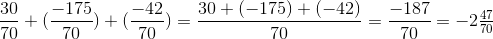 .
.
Câu b
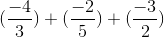 =
= 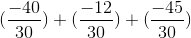 =
= 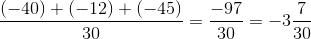 .
.
Câu c
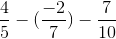 =
= 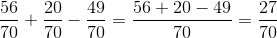 .
.
Câu d
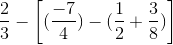 =
=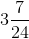 .
.
4. Giải bài 9 trang 10 SGK Toán 7 tập 1
Tìm x, biết
a) \(x+\frac{1}{3} = \frac{3}{4}\)
b) \(x-\frac{2}{5} = \frac{5}{7}\)
c) \(-x - \frac{2}{3}\)
d) \(\frac{4}{7} - x = \frac{1}{3}\)
Phương pháp giải
Áp dụng quy tắc chuyển vế:
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức ta phải đổi dấu số hạng đó
Tổng quát: Với mọi \(x, y , z ∈\mathbb Q\), ta có:
\(x + y = z \Rightarrow x = z-y\).
Hướng dẫn giải
Câu a
x + => x =
Câu b
x - => x =
Câu c
-x - =
=> \(\frac{-2}{3} + \frac{6}{7} = x \Rightarrow x = -\frac{14}{21} + \frac{18}{21} = \frac{4}{21}\)
Câu d
=> \(\frac{4}{7} - \frac{1}{3} = x \Rightarrow x = \frac{12}{21} - \frac{7}{21} = \frac{5}{21}\)
5. Giải bài 10 trang 10 SGK Toán 7 tập 1
Cho biểu thức
\(A = \left( {6 - \dfrac{2}{3} + \dfrac{1}{2}} \right) - \left( {5 + \dfrac{5}{3} - \dfrac{3}{2}} \right)\)\(\, - \left( {3 - \dfrac{7}{3} + \dfrac{5}{2}} \right)\)
Hãy tính giá trị của A theo hai cách
Cách 1: Trước hết tính giá trị của từng biểu thức trong ngoặc.
Cách 2: Bỏ dấu ngoặc rồi nhóm các số hạng thích hợp.
Phương pháp giải
- Áp dụng các công thức cộng, trừ hai số hữu tỉ: Với \(a,\;b,\;m \in Z,\;\;m > 0\) ta có:
\(\begin{array}{l}
\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}\\
\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}
\end{array}\)
- Quy tắc bỏ dấu ngoặc.
Hướng dẫn giải
Cách 1: Tính giá trị từng biểu thức trong ngoặc
\(\begin{array}{l}
A = \left( {6 - \dfrac{2}{3} + \dfrac{1}{2}} \right) - \left( {5 + \dfrac{5}{3} - \dfrac{3}{2}} \right) - \left( {3 - \dfrac{7}{3} + \dfrac{5}{2}} \right)\\
= \left( {\dfrac{{6.6}}{6} - \dfrac{{2.2}}{6} + \dfrac{3}{6}} \right) - \left( {\dfrac{{5.6}}{6} + \dfrac{{5.2}}{6} - \dfrac{{3.3}}{6}} \right) - \left( {\dfrac{{3.6}}{6} - \dfrac{{7.2}}{6} + \dfrac{{5.3}}{6}} \right)\\
= \dfrac{{36 - 4 + 3}}{6} - \dfrac{{30 + 10 - 9}}{6} - \dfrac{{18 - 14 + 15}}{6}\\
= \dfrac{{35}}{6} - \dfrac{{31}}{6} - \dfrac{{19}}{6} = \dfrac{{35 - 31 - 19}}{6}\\
= - \dfrac{{15}}{6} = - \dfrac{5}{2} = - 2\dfrac{1}{2}.
\end{array}\)
Cách 2: Bỏ dấu ngoặc rồi nhóm các số hạng thích hợp
\(\begin{array}{l}
A = \left( {6 - \dfrac{2}{3} + \dfrac{1}{2}} \right) - \left( {5 + \dfrac{5}{3} - \dfrac{3}{2}} \right) - \left( {3 - \dfrac{7}{3} + \dfrac{5}{2}} \right)\\
= 6 - \dfrac{2}{3} + \dfrac{1}{2} - 5 - \dfrac{5}{3} + \dfrac{3}{2} - 3 + \dfrac{7}{3} - \dfrac{5}{2}\\
= \left( {6 - 5 - 3} \right) + \left( { - \dfrac{2}{3} - \dfrac{5}{3} + \dfrac{7}{3}} \right) + \left( {\dfrac{1}{2} + \dfrac{3}{2} - \dfrac{5}{2}} \right)\\=-2 +\dfrac{-2-5+7}{3}+\dfrac{1+3-5}{2}\\
= - 2 + 0 - \dfrac{1}{2} = - \dfrac{5}{2} = - 2\dfrac{1}{2}.
\end{array}\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Tập hợp Q các số hữu tỉ
- doc Giải bài tập SGK Toán 7 Bài 3: Nhân, chia số hữu tỉ
- doc Giải bài tập SGK Toán 7 Bài 4: Giá trị tuyết đối của một số hữu tỉ. Cộng, trừ, nhhân, chia số thập phân
- doc Giải bài tập SGK Toán 7 Bài 5: Lũy thừa của một số hữu tỉ
- doc Giải bài tập SGK Toán 7 Bài 6: Lũy thừa của một số hữu tỉ (tiếp theo)
- doc Giải bài tập SGK Toán 7 Bài 7: Tỉ lệ thức
- doc Giải bài tập SGK Toán 7 Bài 8: Tính chất của dãy tỉ số bằng nhau
- doc Giải bài tập SGK Toán 7 Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- doc Giải bài tập SGK Toán 7 Bài 10: Làm tròn số
- doc Giải bài tập SGK Toán 7 Bài 11: Số vô tỉ. Khái niệm về căn bậc hai
- doc Giải bài tập SGK Toán 7 Bài 12: Số thực
