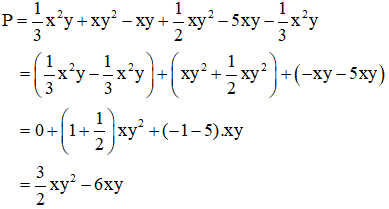Giải bài tập SGK Toán 7 Bài 5: Đa thức
Phần hướng dẫn giải bài tập Bài Đa thức sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung

1. Giải bài 24 trang 38 SGK Toán 7
Ở Đà Lạt, giá táo là \(x\) (đ/kg) và giá nho là \(y\) (đ/kg). Hãy viết biểu thức đại số biểu thị số tiền mua:

a) \(5\) kg táo và \(8\) kg nho.
b) \(10\) hộp táo và \(15\) hộp nho, biết mỗi hộp táo có \(12\) kg và mỗi hộp nho có \(10\) kg.
Mỗi biểu thức tìm được ở hai câu trên có là đa thức không ?
Phương pháp giải
Đọc kĩ đề bài để lập biểu thức thích hợp
Áp dụng công thức:
Số tiền mua \(a\) kg táo = số tiền mua \(1\) kg táo \(\times a\)
Số tiền mua \(n\) kg nho = số tiền mua \(1\) kg nho \(\times b\)
Hướng dẫn giải
Câu a:
Số tiền mua 1kg táo là x đồng. Vậy mua 5kg táo hết \(5.x\) (đồng).
Số tiền mua 1kg nho là y đồng. Vậy mua 8kg nho hết \(8.y\) (đồng).
Gọi \(A\) là số tiền mua \(5\) kg táo và \(8\) kg nho
Ta có: \(A = 5x + 8y\) (đồng)
Câu b:
Mỗi hộp táo có \(12\) kg nên \(10\) hộp có \(10.12 = 120\) kg.
Mỗi hộp nho có \(10\) kg nên \(15\) hộp có \(10.15 = 150\) kg.
Số tiền mua 1kg táo là x đồng. Vậy mua 120kg táo hết \(120.x\) (đồng).
Số tiền mua 1kg nho là y đồng. Vậy mua 150kg nho hết \(150.y\) (đồng).
Nên biểu thức biểu thị số tiền mua \(10\) hộp táo và \(15\) hộp nho là \( B = 120x + 150y\) (đồng)
Các biểu thức \(A; B\) đều là đa thức (vì là tổng của những đơn thức)
2. Giải bài 25 trang 38 SGK Toán 7
Tìm bậc của mỗi đa thức sau:
a) \(3{x^2} - \dfrac{1}{2}x + 1 + 2x - {x^2}\)
b) \(3{x^2} + 7{x^3}-3{x^3} + 6{x^3}-3{x^2}\)
Phương pháp giải
- Thu gọn đa thức đã cho sao cho đa thức không còn hai hạng tử nào đồng dạng.
- Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Hướng dẫn giải
Câu a:
\(3{x^2} - \dfrac{1}{2}x + 1 + 2x - {x^2} \)
\( = \left( {3{x^2} - {x^2}} \right) + \left( { - \dfrac{1}{2}x + 2x} \right) + 1 \)
\(=(3-1)x^2+\left( { - \dfrac{1}{2}+ 2} \right)x+1\)
\( = 2{x^2} + \dfrac{3}{2}x + 1\)
Bậc của các hạng tử trong đa thức là:
Hạng tử \(2{x^2}\) có bậc \(2\)
Hạng tử \(\dfrac{3}{2}x\) có bậc \(1\)
Hạng tử \(1\) có bậc \(0\)
Vậy đa thức đã cho có bậc \(2\).
Câu b:
\(\eqalign{
& 3{x^2} + 7{x^3} - 3{x^3} + 6{x^3} - 3{x^2} \cr
& = \left( {3{x^2} - 3{x^2}} \right) + \left( {7{x^3} + 6{x^3} - 3{x^3}} \right) \cr
& = 10{x^3} \cr} \)
Vậy đa thức đã cho có bậc \(3\).
3. Giải bài 26 trang 38 SGK Toán 7
Thu gọn đa thức sau:
\(Q = {x^2} + {y^2} + {z^2} + {x^2} - {y^2} + {z^2} \)\(\,+ {x^2} + {y^2} - {z^2}\).
Phương pháp giải
Thu gọn đa thức bằng cách thu gọn các đơn thức đồng dạng lại với nhau.
Hướng dẫn giải
\(Q = x^2 + y^2 + z^2 + x^2 – y^2 + z^2 + x^2 + y^2 – z^2\)
\(Q = (x^2 + x^2 + x^2) + (y^2 – y^2 + y^2) + (z^2 – z^2 + z^2)\)
\(Q = 3x^2 + y^2 + z^2\)
4. Giải bài 27 trang 38 SGK Toán 7
Thu gọn rồi tính giá trị của đa thức P tại \(x = 0,5\) và \(y = 1\);
\(P = \dfrac{1}{3}{x^2}y + x{y^2} - xy + \dfrac{1}{2}x{y^2} - 5xy\)\(\, - \dfrac{1}{3}{x^2}y\)
Phương pháp giải
Thu gọn đa thức bằng cách thực hiện phép cộng để thu gọn các hạng tử đồng dạng.
Hướng dẫn giải
Ta có:
Thay \(x = 0,5\) và \(y = 1\) vào đa thức \(P = \dfrac{3}{2}x{y^2} - 6xy\) ta được:
\(P = \dfrac{3}{2}.0,{5.1^2} - 6.0,5.1 = \dfrac{3}{4} - 3 \)\(\,= \dfrac{3}{4} - \dfrac{{12}}{4} = \dfrac{{ - 9}}{4}\)
Vậy \(P\) có giá trị bằng \(\dfrac{-9}{4}\) tại \(x = 0,5\) và \(y = 1\).
5. Giải bài 28 trang 38 SGK Toán 7
Ai đúng? Ai sai?
Bạn Đức đố : "Bậc của đa thức \(M = {x^6} - {y^5} + {x^4}{y^4} + 1\) bằng bao nhiêu ?"
Bạn Thọ nói: "Đa thức \(M\) có bậc là \(6\)".
Bạn Hương nói: "Đa thức \(M\) có bậc là \(5\)".
Bạn Sơn nhận xét: "Cả hai bạn đều sai".
Theo em, ai đúng ? Ai sai ? Vì sao ?
Phương pháp giải
- Tìm bậc của từng hạng tử
- Tìm bậc của đa thức theo quy tắc: Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Hướng dẫn giải
Trong đa thức \(M\), hạng tử \({x^6}\) có bậc \(6\), hạng tử \( - {y^5}\) có bậc \(5\), hạng tử \({x^4}{y^4}\) có bậc \(8\) (vì \( 4 + 4=8\)), hạng tử \(1\) có bậc \(0\). Như vậy: Bậc 8 là bậc cao nhất hay đa thức M là đa thức có bậc 8.
Do đó:
- Bạn Thọ và Hương nói sai.
- Nhận xét của bạn Sơn là đúng.
- Câu trả lời đúng: Đa thức \(M\) có bậc là \(8\).
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Khái niệm về biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 2: Giá trị của một biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 3: Đơn thức
- doc Giải bài tập SGK Toán 7 Bài 4: Đơn thức đồng dạng
- doc Giải bài tập SGK Toán 7 Bài 6: Cộng, trừ đa thức
- doc Giải bài tập SGK Toán 7 Bài 7: Đa thức một biến
- doc Giải bài tập SGK Toán 7 Bài 8: Cộng, trừ đa thức một biến
- doc Giải bài tập SGK Toán 7 Bài 9: Nghiệm của đa thức một biến
- doc Giải bài tập SGK Toán 7 Ôn tập Chương 4: Biểu thức đại số