Giải bài tập SGK Toán 7 Bài 5: Hàm số
Mời các em cùng tham khảo phần hướng dẫn giải bài tập SGK Toán 7 Bài 5: Hàm số. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung

1. Giải bài 24 trang 63 SGK Toán 7
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau:
Đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không?
Phương pháp giải
Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x \) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\) và \(x\) gọi là biến số.
Hướng dẫn giải
Vì mỗi giá trị của \(x\) ta xác định được chỉ một giá trị của \(y\) tương ứng nên đại lượng \(y\) là hàm số của đại lượng \(x\).
2. Giải bài 25 trang 64 SGK Toán 7
Cho hàm số \(y = f\left( x \right) = 3{x^2} + 1\). Tính: \(f\left( {\dfrac{1}{2}} \right), f(1); f(3)\).
Phương pháp giải
Cho hàm số \(y = f(x)\)
Để tính được \(f(a)\) ta thay \(x = a\) vào hàm số để tìm được \(f(a)\).
Hướng dẫn giải
Ta có \(y = f\left( x \right) = 3{x^2} + 1\). Do đó
\(f\left(\dfrac{1}{2} \right) = 3.{\left( \dfrac{1}{2} \right)^2} + 1 = 3.\dfrac{1}{4} + 1 = \dfrac{7}{4}\)
\(f\left( 1 \right) = {3.1^2} + 1 = 3.1 + 1 = 3 + 1 = 4\)
\(f\left( 3 \right) = {3.3^2} + 1 = 3.9 + 1 = 27 + 1 \)\(= 28.\)
3. Giải bài 26 trang 64 SGK Toán 7
Cho hàm số \(y = 5x - 1\). Lập bảng các giá trị tương ứng của \(y\) khi \(x = -5; -4; -3; -2; 0\); \( \dfrac{1}{5}\)
Phương pháp giải
Với từng giá trị của \(x\) ta thay vào hàm số ban đầu để tìm được giá trị \(y\) tương ứng.
Hướng dẫn giải
Ta có \(y = 5x - 1\)
Khi \(x = -5\) thì \(y = 5.(-5) - 1 = -26\)
Khi \(x = -4\) thì \(y = 5.(-4) - 1 = -21\)
Khi \(x = -3\) thì \(y = 5.(-3) - 1 = -16\)
Khi \(x = -2\) thì \(y = 5.(-2) - 1 = -11\)
Khi \(x = 0\) thì \(y = 5.0 - 1 = -1\)
Khi \(x = \dfrac{1}{5}\) thì \(y = 5. \dfrac{1}{5} - 1 = 0\)
Ta có bảng sau:
4. Giải bài 27 trang 64 SGK Toán 7
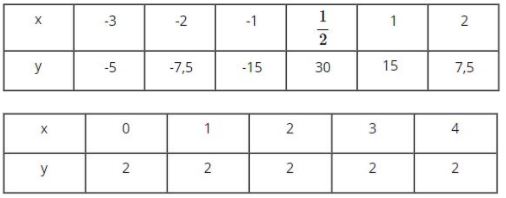
Đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không, nếu bảng các giá tương ứng của chúng là:
Phương pháp giải
Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\) và \(x\) gọi là biến số.
Hướng dẫn giải
a) Vì với mỗi giá trị của \(x\) ta xác định được một giá trị tương ứng của \(y\), nên đại lượng \(y\) là hàm số của đại lượng \(x.\)
b) Với mỗi giá trị của \(x\) ta xác định được một giá trị của \(y\) tương ứng nên \(y\) được gọi là hàm số của \(x.\)
Nhận xét: Với mọi \(x\) thì \(y\) luôn nhận một giá trị là \(2\) nên đây là một hàm hằng.
5. Giải bài 28 trang 64 SGK Toán 7
Cho hàm số \(y = f\left( x \right) =\dfrac{{12}}{x}\)
a) Tính \(f(5); f(-3).\)
b) Hãy điền các giá trị tương ứng của hàm số vào bảng sau:
Phương pháp giải
a) Để tính \(f(5); f(-3)\) thì ta thay \(x = 5; x = -3\) vào hàm số ban đầu để tìm được giá trị \(y\) tương ứng.
b) Để tìm được giá trị \(y\) tương ứng trong bảng thì ta thay từng giá trị \(x\) vào hàm số ban đầu để tìm.
Hướng dẫn giải
Ta có: \(y = f\left( x \right) = \dfrac{{12}}{x}\)
Câu a: \(f\left( 5 \right) =\dfrac{{12}}{5} = 2,4\)
\( f\left( { - 3} \right) = \dfrac{{12}}{{ - 3}} = - 4\)
Câu b: Thay lần lượt \(x\) bởi \(-6, -4 ; -3 ; 2 ; 5 ; 6 ; 12\) vào công thức \(f(x)=\dfrac{{12}}{x}\) ta được:
\(\eqalign{
& f\left( { - 6} \right) = {{12} \over { - 6}} = - 2 \cr
& f\left( { - 4} \right) = {{12} \over { - 4}} = - 3 \cr
& f\left( { - 3} \right) = {{12} \over { - 3}} = - 4 \cr
& f\left( 2 \right) = {{12} \over 2} = 6 \cr
& f\left( 5 \right) = {{12} \over 5} = 2,4 \cr
& f\left( 6 \right) = {{12} \over 6} = 2 \cr
& f\left( {12} \right) = {{12} \over {12}} = 1 \cr} \)
Ta được bảng sau:
6. Giải bài 29 trang 64 SGK Toán 7
Cho hàm số \(y = f\left( x \right) = {x^2} - 2\) . Hãy tính: \(f(2); f(1); f(0); f(-1); f(-2)\)
Phương pháp giải
Thay từng giá trị \(x\) vào hàm số ban đầu ta tìm được các giá trị \(y\) tương ứng với giá trị \(x\) đó.
Hướng dẫn giải
Ta có: \(y = f\left( x \right) = {x^2} - 2\)
Thay \(x=2; 1; 0; -1; -2\) vào hàm số ta được:
\(f\left( 2 \right) = {2^2} - 2 = 4 - 2 = 2\)
\(f\left( 1 \right) = {1^2} - 2 = 1 - 2 = -1\)
\(f\left( 0 \right) = {0^2} - 2 = - 2\)
\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2 = 1 - 2 = - 1\)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} - 2 = 4 - 2 = 2\)
7. Giải bài 30 trang 64 SGK Toán 7
Cho hàm số \(y = f(x) = 1 – 8x.\) Khẳng định nào sau đây là đúng:
a) \(f(-1) = 9?\)
b) \(f\left( \dfrac{1}{2} \right) = - 3?\)
c) \( f(3) = 25?\)
Phương pháp giải
Ta thay lần lượt \(x = -1; x = \dfrac{1}{2}; x = 3\) vào hàm số ban đầu sau đó tìm được \(y\) đối chiếu với kết quả vế phải. Nếu bằng nhau thì khẳng định đó đúng.
Hướng dẫn giải
Hàm số \( y = f(x) = 1 – 8x \)
Câu a: \( f(-1) = 1 - 8.(-1) = 1 + 8 = 9\) nên khẳng định \( f(-1) = 9\) đúng.
Câu b: \(f\left( \dfrac{1}{2} \right) = 1 - 8.\dfrac{1}{2}= 1 - 4 = - 3\)
\( \Rightarrow \) Khẳng định \(f\left( \dfrac{1}{2} \right) = - 3\) đúng.
Câu c: \( f(3) = 1 - 8. 3 = 1 - 24 = -23 \ne 25\) nên khẳng định \( f(3) = 25 \) sai.
8. Giải bài 31 trang 65 SGK Toán 7
Cho hàm số \(y = \dfrac{2}{3}x\). Điền số thích hợp vào ô trống trong bảng sau:
Phương pháp giải
Để tìm \(y\): ta thay từng giá trị \(x\) vào hàm số ban đầu ta tìm được \(y\) tương ứng.
Để tìm \(x\): ta thay từng giá trị \(y\) vào hàm số ban đầu ta tìm được \(x\) tương ứng.
Hướng dẫn giải
Ta có: \(y = \dfrac{2}{3}x\) nên:
\(\eqalign{
& x = - 0,5 \Rightarrow y = {2 \over 3}.(-0,5) = {2 \over 3}.{-1 \over 2} = {-1 \over 3} \cr
& y = - 2 \Rightarrow - 2 = {2 \over 3}x \Rightarrow x = - 2:{2 \over 3} = \left( { - 2} \right).{3 \over 2} = - 3 \cr
& y = 0 \Rightarrow 0 = {2 \over 3}x \Rightarrow x = 0:{2 \over 3} = 0 \cr
& x = 4,5 \Rightarrow y = {2 \over 3}.4,5 = {2 \over 3}.{9 \over 2} = 3 \cr
& x = 9 \Rightarrow y = {2 \over 3}.9 = 6 \cr} \)
Ta được bảng sau:
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Đại lượng tỉ lệ thuận
- doc Giải bài tập SGK Toán 7 Bài 2: Một số bài toán về đại lượng tỉ lệ thuận
- doc Giải bài tập SGK Toán 7 Bài 3: Đại lượng tỉ lệ nghịch
- doc Giải bài tập SGK Toán 7 Bài 4: Một số bài toán về đại lượng tỉ lệ nghịch
- doc Giải bài tập SGK Toán 7 Bài 6: Mặt phẳng tọa độ
- doc Giải bài tập SGK Toán 7 Bài 7: Đồ thị hàm số y = ax (a # 0)
- doc Giải bài tập SGK Toán 7 Ôn tập chương 2: Hàm số và đồ thị
.JPG)
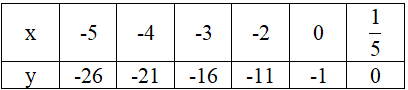
.JPG)
.JPG)
.JPG)
.JPG)
