Giải bài tập SGK Toán 7 Bài 6: Tính chất ba đường phân giác của tam giác
Hướng dẫn Giải bài tập SGK Toán 7 Bài Tính chất ba đường phân giác của tam giác sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 36 trang 72 SGK Hình học 7
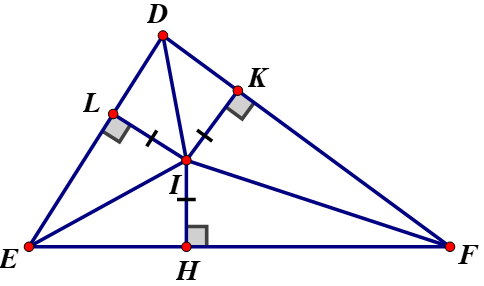
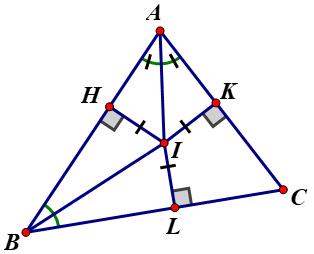
Cho tam giác \(DEF\), điểm \(I\) nằm trong tam giác và cách đều ba cạnh của nó. Chứng minh \(I\) là điểm chung của ba đường phân giác của tam giác \(DEF.\)
Phương pháp giải
- Chứng minh 1 lần lượt nằm trên tia phân giác của ba góc D, E, F.
- Áp dụng Định lý 2 (đảo): Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên phân giác của góc đó.
Hướng dẫn giải
Từ điểm \(I\) ta kẻ \(IA ⊥ DE; IB ⊥ EF\) và \(IC ⊥ DF.\)
- Vì điểm \(I\) cách đều hai cạnh \(DE\) và \(DF\) nên \(I\) nằm trên đường phân giác của góc \(EDF\) (định lí 2 - định lí đảo của tia phân giác một góc)
- Vì điểm \(I\) cách đều hai cạnh \(FD\) và \(FE\) nên \(I\) nằm trên đường phân giác của góc \(EFD\) (định lí 2 - định lí đảo của tia phân giác một góc)
- Vì điểm \(I\) cách đều hai cạnh \(EF\) và \(ED\) nên \(I\) nằm trên đường phân giác của góc \(DEF\) (định lí 2 - định lí đảo của tia phân giác một góc)
Vậy \(I\) là điểm chung của ba đường phân giác của tam giác \(DEF.\)
2. Giải bài 37 trang 73 SGK Hình học 7
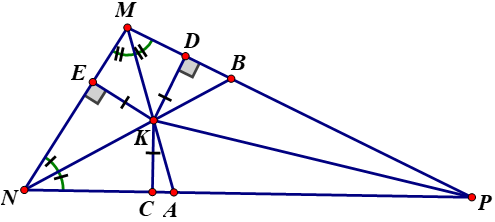
Nêu cách vẽ điểm \(K\) ở trong tam giác \(MNP\) mà các khoảng cách từ \(K\) đến ba cạnh của tam giác đó bằng nhau. Vẽ hình minh họa.
Phương pháp giải
- Áp dụng định lí: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
- Từ đó suy ra K là giao điểm của 3 tia phân giác của tam giác MNP.
- Vẽ hai trong ba tia phân phác của ba góc M, N, P.
Hướng dẫn giải
- Cách vẽ: Vẽ tia phân giác \(MS\) của góc \(M\), tia phân giác \(NQ\) của góc \(N\). Giao điểm của hai tia phân giác chính là điểm \(K\) cần vẽ.
- Chứng minh:
Vì \(K\) là giao điểm của hai đường phân giác trong tam giác \(MNP\) nên \(K\) là giao của ba đường phân giác của tam giác \(MNP\).
Do đó \(K\) cách đều ba cạnh của tam giác \(MNP\) (Theo định lí tính chất của ba đường phân giác trong tam giác).
3. Giải bài 38 trang 73 SGK Hình học 7
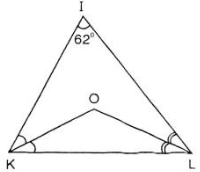
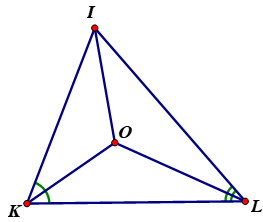
Cho hình 38.
a) Tính góc \(KOL\).
b) Kẻ tia \(IO\), hãy tính góc \(KIO\).
c) Điểm \(O\) có cách đều ba cạnh của tam giác \(IKL\) không? Tại sao?
Phương pháp giải
- Áp dụng tính chất tia phân giác của một góc chia góc đó thành hai góc bằng nhau và bằng \(\dfrac{1}{2}\) góc đó.
- Định lí về tổng ba góc trong tam giác: Tổng ba góc của một tam giác bằng \(180^0\)
- Áp dụng tính chất ba đường phân giác của tam giác: Ba đường phân giác của một tam giác cùng cắt nhau tại một điểm. Điểm đó cách đều ba cạnh của tam giác.
Hướng dẫn giải
Câu a:
\(∆KIL\) có \(\widehat{I} + \widehat{IKL}+ \widehat{ILK} =180^o\) (Theo định lí tổng ba góc trong một tam giác)
Mà \(\widehat{I} =62^o\) nên \(\widehat{IKL}+ \widehat{ILK} = 180^o - 62^o = 118^o \)
Vì \(KO\) và \(LO\) lần lượt là phân giác \(\widehat{IKL}\), \(\widehat{ILK}\) nên \(\widehat {OKL} = \dfrac{1}{2}\widehat {IKL},\,\,\widehat {OLK} = \dfrac{1}{2}\widehat {ILK}\)
Suy ra \(\widehat{OKL}+ \widehat{OLK}= \dfrac{1}{2}(\widehat{IKL}+ \widehat{ILK})\)
\(\Rightarrow\) \(\widehat{OKL}+ \widehat{OLK} = \dfrac{1}{2}. 118^o\)
\(\Rightarrow\) \(\widehat{OKL}+ \widehat{OLK} = 59^o\)
\(∆KOL\) có \(\widehat{OKL}+ \widehat{OLK} + \widehat{KOL} =180^o \) (Theo định lí tổng ba góc trong một tam giác)
Mà \(\widehat{OKL}+ \widehat{OLK} = 59^o\) nên \(\widehat{KOL} = 180^o -59^o = 121^o\)
Câu b:
\(ΔKIL\) có \(O\) là giao điểm của hai đường phân giác \(KO\) và \(LO\) nên \(IO\) là đường phân giác của góc \(KIL\) (định lí ba đường phân giác cùng đi qua một điểm).
Do đó: \( \widehat{KIO} = \dfrac{\widehat{KIL}}{2}= \dfrac{62^0}{2} = 31^o\)
Câu c:
Vì \(O\) là giao điểm của ba đường phân giác của tam giác \(IKL\) nên \(O\) cách đều ba cạnh của tam giác \(IKL\). (Theo định lí về tính chất của ba đường phân giác trong tam giác)
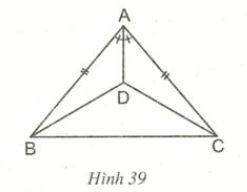
4. Giải bài 39 trang 73 SGK Hình học 7
Cho hình \(39.\)
a) Chứng minh \(∆ABD = ∆ACD.\)
b) So sánh góc \(DBC\) với góc \(DCB.\)
Phương pháp giải
- Chứng minh \(∆ABD = ∆ACD\) theo trường hợp bằng nhau thứ hai của tam giác.
- Chứng minh tam giác \(BDC\) là tam giác cân, từ đó suy ra \(\widehat{DBC}= \widehat{DCB}\).
Hướng dẫn giải
Câu a:
Xét \(∆ABD\) và \(∆ACD\) ta có:
\(AB = AC\) (giả thiết)
\(\widehat{BAD}= \widehat{CAD}\) (giả thiết)
\(AD\) cạnh chung
Vậy \(∆ABD = ∆ACD\) (c.g.c)
Câu b:
Vì \(∆ABD = ∆ACD\) (chứng minh trên)
\( \Rightarrow BD = CD \) ( \(2\) cạnh tương ứng)
\( \Rightarrow ∆BCD\) cân tại \(D\)
\( \Rightarrow \) \(\widehat{DBC}= \widehat{DCB}\) ( tính chất tam giác cân) (điều phải chứng minh).
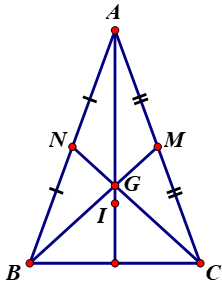
5. Giải bài 40 trang 73 SGK Hình học 7
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(G\) là trọng tâm, \(I\) là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm \(A, G, I\) thẳng hàng.
Phương pháp giải
- Chứng minh ba điểm \(A, G, I\) cùng nằm trên một đường thẳng đó chính là đường trung tuyến đồng thời là tia phân giác của góc BAC.
- Áp dụng tính chất: Trong một tam giác cân hai đường trung tuyến úng với hai cạnh bên bằng nhau.
- Áp dụng tính chất trọng tâm của tam giác.
- Chứng minh G nừm trên tia phân giác của góc BAC.
Hướng dẫn giải
Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB = \frac{2}{3}BM;\,\,\,GC = \frac{2}{3}CN\) (Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\( \Rightarrow \widehat {BAG} = \widehat {CAG}\) (hai góc tương ứng)
\( \Rightarrow G\) thuộc tia phân giác của \(\widehat {BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat {BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat {BAC}\) nên A, G, I thẳng hàng
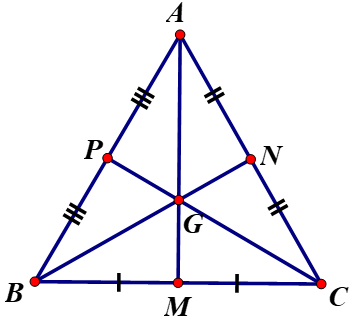
6. Giải bài 41 trang 73 SGK Hình học 7
Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?
Phương pháp giải
- Chứng minh G thuộc 2 trong 2 tia phân giác của 3 góc A, B, C.
- Áp dụng kết quả của bài 40: Tam giác ABC cân thì Trọng tâm G của tam giác ABC nằm trên tia phân phân giác của góc BAC.
- Tương tự suy ra G cũng nằm trên tia phân giác của góc ABC, góc ACB.
Hướng dẫn giải
Giả sử \(∆ABC\) đều có trọng tâm \(G\). Các điểm \(E, N, M\) lần lượt là trung điểm của \(AB, BC, AC.\)
Áp dụng kết quả của bài 40: Tam giác ABC cân thì Trọng tâm G của tam giác ABC nằm trên tia phân phân giác của góc BAC.
Do đó G cách đều hai cạnh AB và AC.
Vì tam giác ABC đều nên tam giác ABC cân tại 3 đỉnh A, B, C.
Xét tam giác ABC cân tại B có G là trọng tâm thì G cũng nằm trên tia phân giác của góc ABC.
Suy ra G cách đều hai cạnh AB và BC.
Vậy G cánh đều ba cạnh của tam giác ABC.
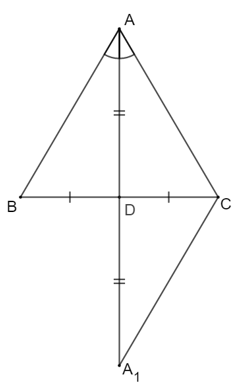
7. Giải bài 42 trang 73 SGK Hình học 7
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
Phương pháp giải
Trong \(∆ABC\), nếu \(AD\) vừa là đường trung tuyến vừa là đường phân giác thì kéo dài \(AD\) một đoạn \(D{A_1}\) sao cho \(D{A_1}= AD.\)
Hướng dẫn giải
Gọi \(AD\) là đường trung tuyến đồng thời là đường phân giác của góc \(A\) trong \(ΔABC.\) Ta chứng minh \(∆ABC\) cân tại \(A.\)
Kéo dài \(AD\) một đoạn \(D{A_1}= AD.\)
Xét \(∆ADC\) và \(∆{A_1}DB\) ta có:
\(DC = DB\) (do \(AD\) là trung tuyến)
\({ \widehat{D}}_1 = {\widehat{D}}_2 \) (\(2\) góc đối đỉnh)
\(AD = D{A_1}\) (do cách vẽ)
Vậy \(∆ADC = ∆{A_1}DB\) (c.g.c)
\(\Rightarrow AC = {A_1}B\) (1)
và \(\widehat{DAC}= \widehat{DA_1B}\)
Mà \(\widehat{BAD}= \widehat{DAC}\) (Vì \(AD\) là phân giác)
\(\Rightarrow \) \(\widehat{BAD}=\widehat{DA_1B}\)
Xét tam giác \(AB{A_1}\) có \( \widehat{DA_1B} = \widehat{BAD}\)
Vậy tam giác \(AB{A_1}\) cân tại \(B\)
\(\Rightarrow AB = {A_1}B\) (2)
Từ (1) và (2) suy ra \(AB = AC\).
Vậy \(∆ABC\) cân tại \(A.\)
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
8. Giải bài 43 trang 73 SGK Hình học 7
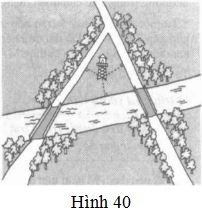
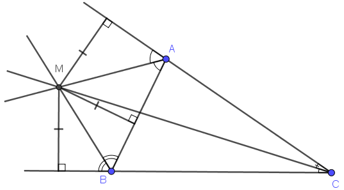
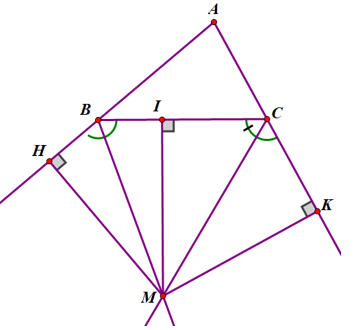
Đố: Có hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau (h. \(40\)).
Hãy tìm một địa điểm để xây dựng một đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhau. Có tất cả mấy địa điểm như vậy?
Phương pháp giải
- Hai con đường và dòng sôngcắt nhau tạo thành một tam giác.
- Xét hai trường hợp đài quan sát nằm trong hoặc nằm ngoài tam giác
- Áp dụng tính chất ba đường phân giác của tam giác: Ba đường phân giác của một tam giác cùng cắt nhau tại một điểm. Điểm đó cách đều ba cạnh của tam giác.
Hướng dẫn giải
Hai con đường cắt nhau và cùng cắt một con sông tạo thành tam giác ABC.
Vì khoảng cách từ điểm cần xây đến hai con đường và bờ sông là như nhau nên địa điểm để xây dựng đài quan sát thỏa mãn đề bài có thể là
- TH1: Giao điểm của ba đường phân giác trong của tam giác ABC.
- TH2: Giao điểm M của hai tia phân giác ngoài và một tia phân giác trong. Ta có ba điểm M như vậy.
Vậy có tất cả 4 điểm có thể xây dựng đài quan sát thỏa mãn điều kiện.
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Giải bài tập SGK Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Giải bài tập SGK Toán 7 Bài 3: Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- doc Giải bài tập SGK Toán 7 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Giải bài tập SGK Toán 7 Bài 5: Tính chất tia phân giác của một góc
- doc Giải bài tập SGK Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Giải bài tập SGK Toán 7 Bài 8: Tính chất đường trung trực của tam giác
- doc Giải bài tập SGK Toán 7 Bài 9: Tính chất ba đường cao của tam giác
- doc Giải bài tập SGK Toán 7 Ôn tập chương 3: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác