Giải bài tập SGK Toán 7 Bài 3: Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
Phần hướng dẫn giải bài tập Bài Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung

1. Giải bài 15 trang 63 SGK Hình học 7
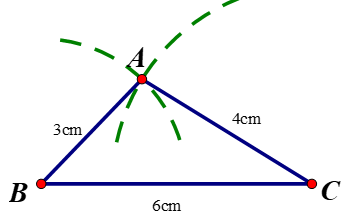
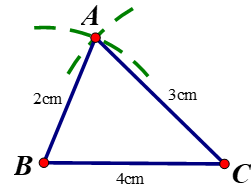
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong các trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế:
a) \(2\,cm, 3\,cm, 6\,cm.\)
b) \(2\,cm, 4\,cm, 6\,cm.\)
c) \(3\,cm, 4\,cm, 6\,cm.\)
Phương pháp giải
- Khi xét độ dài ba đoạn thẳng có thỏa mãn bất đẳng thức tam giác hay không ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại.
- Định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hướng dẫn giải
Câu a:
Ta có \(6-3=3>2\), do đó ba độ dài \(2\,cm, 3\,cm, 6\,cm\) không là ba cạnh của tam giác.
Câu b:
Vì \(6 = 2 + 4\) nên ba độ dài là \(2\,cm, 4\,cm, 6\,cm\) không là ba cạnh của một tam giác.
Câu c:
Ta có: \(4 - 3 < 6 < 4 + 3\), do đó ba độ dài \(3\,cm, 4\,cm, 6\,cm\) là ba cạnh của một tam giác.
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A.
- Nối AB, AC ta được tam giác cần dựng.
2. Giải bài 16 trang 63 SGK Hình học 7
Cho tam giác \(ABC\) với hai cạnh \(BC = 1\,cm, AC = 7\,cm\). Hãy tìm độ dài cạnh \(AB\), biết rằng độ dài này là một số nguyên (cm). Tam giác \(ABC\) là tam giác gì?
Phương pháp giải
- Áp dụng hệ quả bất đẳng thức tam giác: Trong một tam giác, độ dài một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại và bé hơn tổng độ dài hai cạnh đó.
- So sánh độ dài 3 cạnh của tam giác để kết luận tam giác ABC là tam giác gì.
Hướng dẫn giải
Trong tam giác \(ABC\), theo bất đẳng thức tam giác ta có:
\( AC - BC < AB < AC + BC\)
Thay độ dài \(BC = 1\,cm, AC = 7\,cm\) ta được:
\(7 - 1 < AB < 7 + 1\)
\(6 < AB < 8\) (1)
Vì độ dài \(AB\) là một số nguyên thỏa mãn (1) nên \(AB = 7\,cm.\)
Do đó \(∆ABC\) cân tại \(A\) vì \(AB = AC = 7\,cm.\)
3. Giải bài 17 trang 63 SGK Hình học 7
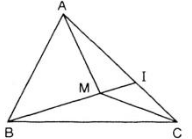
Cho tam giác \(ABC\) và \(M\) là một điểm nằm trong tam giác. Gọi \(I\) là giao điểm của đường thẳng \(BM\) và cạnh \(AC\).
a) So sánh \(MA\) với \(MI + IA\), từ đó chứng minh \(MA + MB < IB + IA.\)
b) So sánh \(IB\) với \(IC + CB\), từ đó chứng minh \(IB + IA < CA + CB\).
c) Chứng minh bất đẳng thức \(MA + MB < CA + CB.\)
Phương pháp giải
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
- Áp dụng tính chất của bất phương trình: Nếu X< Y thì X + Z < Y + Z.
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hướng dẫn giải
Câu a:
\( M\) nằm trong tam giác \(ABC\) nên ba điểm \(A, M, I\) không thẳng hàng.
Áp dụng bất đẳng thức tam giác vào \(∆AMI\) ta có:
\(MA < MI + IA\) (1)
Cộng \(MB\) vào hai vế của (1) ta được:
\(MA + MB < MB + MI + IA\)
Mà \(MB + MI = IB\)
\(\Rightarrow MA + MB < IB + IA\) (điều phải chứng minh).
Câu b:
Ba điểm \(B, I, C\) không thẳng hàng.
Áp dụng bất đẳng thức tam giác vào \(∆BIC\) ta có:
\(IB < IC + BC\) (2).
Cộng \(IA\) vào hai vế của (2) ta được:
\(IB + IA < IA + IC + BC\)
Mà \(IA + IC = AC\)
\(\Rightarrow IB + IA < AC + BC\) (điều phải chứng minh).
Câu c:
Vì \(MA + MB < IB + IA\) (chứng minh trên)
\(IB + IA < AC + BC\) (chứng minh trên)
Suy ra \(MA + MB < CA + CB\) (điều phải chứng minh).
4. Giải bài 18 trang 63 SGK Hình học 7
Cho các bộ ba đoạn thẳng có độ dài như sau:
a) \(2\,cm; 3\,cm; 4\,cm\)
b) \(1\,cm; 2\,cm; 3,5\,cm\)
c) \(2,2\,cm; 2\,cm; 4,2\,cm\)
Hãy vẽ tam giác có độ dài ba cạnh lần lượt là một trong các bộ ba ở trên (nếu vẽ được). Trong trường hợp không vẽ được, hãy giải thích.
Phương pháp giải
- Khi xét độ dài ba đoạn thẳng có thỏa mãn bất đẳng thức tam giác hay không ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại.
- Định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hướng dẫn giải
Câu a:
Ba độ dài \(2\,cm, 3\,cm, 4\,cm\) thỏa mãn bất đẳng thức: \(3 - 2 < 4 < 3 + 2\) nên chúng là ba cạnh của tam giác.
Dựng tam giác có độ dài ba cạnh là \(2\,cm, 3\,cm, 4\,cm\)
- Vẽ \(BC = 4\,cm\)
- Dựng cung tròn tâm \(B\) bán kính \(2\,cm\) ; cung tròn tâm \(C\) bán kính \(3\,cm\). Hai cung tròn cắt nhau tại \(A\).
- Nối \(AB, AC\) ta được tam giác \(ABC\) cần dựng.
Câu b:
Vì \(1cm+2cm < 3,5cm\) nên bộ ba đoạn thẳng có độ dài \(1\,cm; 2\,cm; 3,5\,cm\) không là ba cạnh của tam giác.
Câu c:
Vì \(2,2cm + 2cm = 4,2cm\) nên bộ ba đoạn thẳng có độ dài \(2,2\,cm; 2\,cm; 4,2\,cm\) không là ba cạnh của tam giác.
5. Giải bài 19 trang 63 SGK Hình học 7
Tìm chu vi của một tam giác cân biết độ dài hai cạnh của nó là \(3,9\,cm\) và \(7,9\,cm.\)
Phương pháp giải
Áp dụng bất đẳng thức tam giác để xác định độ dài cạnh bên và cạnh đáy của tam giác cân: Trong một tam giác, độ dài một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại và bé hơn tổng độ dài hai cạnh đó.
- Chu vi tam giác là tổng độ dài 3 cạnh của tam giác đó.
Hướng dẫn giải
Theo đề bài, tam giác đã cho là tam giác cân và hai cạnh của nó là \(3,9\,cm\) và \(7,9,cm.\)
Suy ra, cạnh bên của tam giác có thể có độ dài là 3,9cm hoặc 7,9cm.
TH1: Giả sử cạnh bên có độ dài là 3,9cm
Vì \(3,9cm + 3,9cm = 7,8cm < 7,9cm\) (không thỏa mãn bất đẳng thức tam giác) nên loại
TH2: Giả sử cạnh bên có độ dài là 7,9cm
Vì \(3,9cm + 7,9cm = 11,8cm > 7,9cm\) (thỏa mãn bất đẳng thức tam giác) nên nhận
Vậy tam giác cân có độ dài cạnh bên là \(7,9\,cm\) và độ dài cạnh đáy là \(3,9\,cm.\)
Chu vi tam giác đó là:
\(3,9 + 7,9 +7,9= 19,7\; (cm)\)
6. Giải bài 20 trang 64 SGK Hình học 7
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác \(ABC\). Giả sử \(BC\) là cạnh lớn nhất. Kẻ đường vuông góc \(AH\) đến đường thẳng \(BC\) (\(H \in BC\)).
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở bài 1 để chứng minh \(AB + AC > BC.\)
b) Từ giả thiết về cạnh \(BC\), hãy suy ra hai bất đẳng thức tam giác còn lại.
Phương pháp giải
- Áp dụng nhận xét trong tam giác vuông thì cạnh huyền là cạnh lớn nhất.
Hướng dẫn giải
Câu a:
\(∆ABC\) có cạnh \(BC\) lớn nhất nên chân đường vuông góc kẻ từ \(A\) phải nằm giữa \(B\) và \(C\)
Hay \(H\) nằm giữa \(B\) và \(C\) \(\Rightarrow HB + HC = BC\)
Trong \(∆AHC\) vuông tại \(H\) ta có: \(HC < AC\) (1) (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất)
Trong \(∆AHB\) vuông tại \(H\) ta có: \(HB < AB\) (2) (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất)
Cộng theo vế hai bất đẳng thức (1), (2) ta có:
\(HB + HC < AC + AB\)
Vì \(HB + HC = BC\) nên \(BC < AC + AB.\)
Câu b:
\(BC\) là cạnh lớn nhất nên suy ra \(AB < BC\) và \(AC < BC\)
Vì \(AB, AC > 0\) nên ta có: \(AB < BC + AC; AC < BC + AB\)
7. Giải bài 21 trang 64 SGK Hình học 7
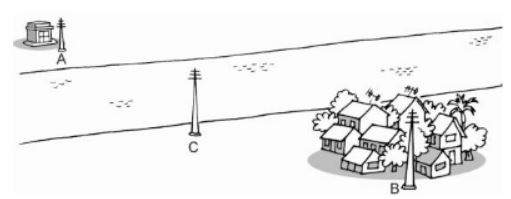
Một trạm biến áp và một khu dân cư được xây dựng cách xa hai bờ sông tại địa điểm \(A\) và \(B\).
Hãy tìm trên bờ sông gần khu dân cư một địa điểm \(C\) để xây dựng một cột mắc dây đưa điện từ trạm biến áp về cho khu dân cư sao cho độ dài đường dây dẫn là gần nhất.
Phương pháp giải
Dựa vào định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hướng dẫn giải
- Nếu \(C\) nằm trên đoạn thẳng \(AB\) (A, B, C thẳng hàng), tức là:
\(AC + BC = AB\) (1)
- Nếu \(A,B,C\) không thẳng hàng thì ba điểm \(A, B, C\) tạo thành một tam giác \(ABC\). Theo bất đẳng thức tam giác ta có:
\(AC + BC > AB\) (2)
Từ (1) và (2) suy ra \(AC+BC \ge AB\)
Do đó \(AC + BC\) ngắn nhất khi \(C\) nằm giữa \(A\) và \(B.\)
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là \(C\) nằm giữa \(A\) và \(B\) (\(A,B,C\) thẳng hàng).
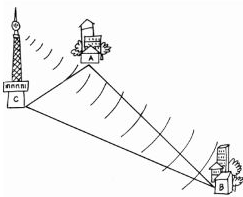
8. Giải bài 22 trang 64 SGK Hình học 7
Ba thành phố \(A, B, C\) là ba đỉnh của một tam giác; biết rằng \(AC = 30\,km, AB = 90\,km\) (hình dưới)
a) Nếu đặt ở \(C\) máy phát sóng truyền thanh có bán kính hoạt động bằng \(60\,km\) thì thành phố \(B\) có nhận được tín hiệu không? Vì sao?
b) Cũng câu hỏi như vậy với máy phát sóng có bán kính hoạt động bằng \(120 \,km.\)
Phương pháp giải
Dựa vào hệ quả: Trong một tam giác, một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại và nhỏ hơn tổng độ dài hai cạnh còn lại.
Hướng dẫn giải
Áp dụng hệ quả của bất đẳng thức tam giác vào tam giác \(ABC\) ta có:
\(AB - AC < BC < AB + AC\)
Thay số ta được: \(90 - 30 < BC < 90 + 30\)
hay \(60 < BC < 120\)
Câu a:
Vì \(BC > 60\) nên nếu đặt tại \(C\) máy phát sóng truyền thanh có bán kính hoạt động bằng \(60\,km\) thì thành phố \(B\) không nhận được tín hiệu.
Câu b:
Vì \(BC < 120\) nên nếu đặt tại \(C\) máy phát sóng truyền thanh có bán kính hoạt động bằng \(120\,km\) thì thành phố \(B\) nhận được tín hiệu.
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Giải bài tập SGK Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Giải bài tập SGK Toán 7 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Giải bài tập SGK Toán 7 Bài 5: Tính chất tia phân giác của một góc
- doc Giải bài tập SGK Toán 7 Bài 6: Tính chất ba đường phân giác của tam giác
- doc Giải bài tập SGK Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Giải bài tập SGK Toán 7 Bài 8: Tính chất đường trung trực của tam giác
- doc Giải bài tập SGK Toán 7 Bài 9: Tính chất ba đường cao của tam giác
- doc Giải bài tập SGK Toán 7 Ôn tập chương 3: Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác