Toán 10 Chương 1 Bài 1: Các định nghĩa

Định nghĩa: Vectơ là một đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.

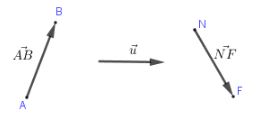
Vectơ có điểm đầu là \(A\), điểm cuối \(B\) kí hiệu \(\overrightarrow{AB}\) và đọc là "vectơ \(AB\)". Khi không cần chỉ rõ điểm đầu, điểm cuối vectơ còn được kí hiệu \(\overrightarrow{a}\), \(\overrightarrow{b}\)...

Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.

Vectơ không: Vectơ có điểm đầu trùng với điểm cuối, ta gọi là vectơ-không.

Định nghĩa: Hai vectơ được gọi là cùng phương khi và chỉ khi chúng có giá song song hoặc trùng nhau.

Nếu hai vectơ cùng phương thì hoặc là chúng cùng hướng, hoặc là chúng ngược hướng.

Ví dụ:

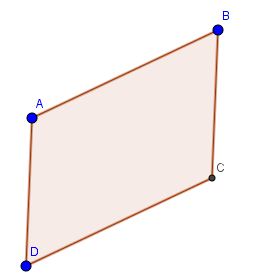
Cho hình bình hành ABCD. chúng ta có các nhận xét sau:

\(AB=CD;AD=BC\)

Vì vậy, ta kết luận: \(\vec{AB}=\vec{DC}; \vec{AD}=\vec{BC}\)

Và \(\vec{AB}=-\vec{CD}; \vec{AD}=-\vec{CB}\).

Định nghĩa

• Hai vectơ được gọi là bằng nhau khi chúng cùng hướng và cùng độ dài.

• Nếu hai vectơ \(\vec{a}\) và \(\vec{b}\) bằng nhau thì ta viết \(\vec{a}=\vec{b}\).

Câu 1: Với hai điểm A, B phân biệt ta có được bao nhiêu vectơ có điểm đầu và điểm cuối là A hoặc B.

Hướng dẫn giải

Với hai điểm A, B phân biệt ta có được 2 vectơ có điểm đầu và điểm cuối là A hoặc B.

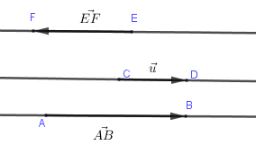
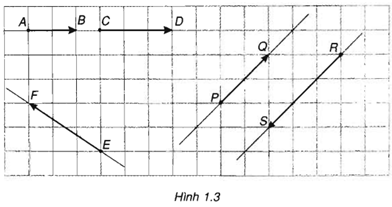
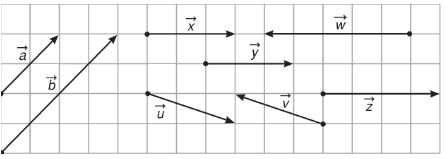
Câu 2: Hãy nhận xét về vị trí tương đối của các giá của các cặp vectơ sau: \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \), \(\overrightarrow {EF} \) và \(\overrightarrow {PQ} \).

Hướng dẫn giải

Quan sát hình vẽ ta thấy:

Giá của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) trùng nhau, cùng có hướng từ trái sang phải.

Giá của hai véc tơ \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) song song, hướng ngược nhau (\(\overrightarrow {PQ} \) hướng lên, \(\overrightarrow {RS} \) hướng xuống).

Giá của hai véc tơ \(\overrightarrow {EF} \) và \(\overrightarrow {PQ} \) cắt nhau.

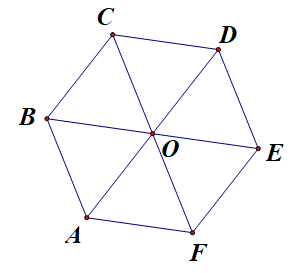
Câu 3: Gọi O là tâm hình lục giác đều ABCDEF. Hãy chỉ ra các vectơ bằng \(\overrightarrow {OA} \)

Hướng dẫn giải

Vectơ bằng vectơ \(\overrightarrow {OA} \) là vectơ \(\overrightarrow {DO} \), \(\overrightarrow {CB} \), \(\overrightarrow {EF} \).

Câu 1: Hãy nêu những điểm khác nhau giữa vectơ và tia?

Câu 2: Cho lục giác đều ABCDEF tâm O, viết các vectơ bằng với vectơ \(\vec {BC}\)

Câu 1: Khẳng định nào là không đúng?

A. Nếu hai vectơ khác vectơ không cùng hướng với nhau thì có giá song song hoặc trùng nhau

B. Vectơ không cùng phương với mọi vectơ

C. Hai vectơ có cùng phương với vectơ thứ ba thì chúng cùng hướng

D. Hai vectơ khác vectơ không ngược hướng nhau thì cùng phương

Câu 2: Cho đoạn thẳng AB có trung điểm M. Hãy tìm khẳng định đúng?

A. \(\vec{AM}=\vec{BM}\)

B. \(\vec{AM}=-\vec{BM}\)

C. \(\vec{AM}=\vec{AB}\)

D. \(\vec{AM}=-\vec{AB}\)

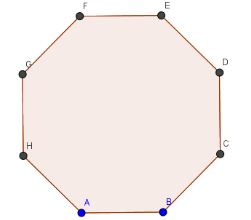
 Câu 3: Cho bát giác đều ABCDEFGH. Vectơ bằng với vectơ \(\overrightarrow {BC} \) là:

A. \(\overrightarrow {FG} \)

B. \(\overrightarrow {ED} \)

C. \(\overrightarrow {DE} \)

D. \(\overrightarrow {GF} \)

Câu 4: Trong hình bên có số cặp vectơ bằng nhau là:

A. 1

B. 2

C. 3

D. 4

Câu 5: Cho bát giác đều ABCDEFGH tâm I. Có bao nhiêu vectơ khác vectơ không, cùng phương với vectơ \(\overrightarrow {AB} \) và nhận các đỉnh của bát giác là gốc và ngọn?

A. 1

B. 3

C. 5

D. 7

Câu 6: Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?

A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các đỉnh của ngũ giác.

B. Có 5 vectơ gốc O có độ dài bằng nhau.

C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác.

D. Các vectơ khác 0→ có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau

Câu 7: Cho 3 điểm phân biệt A, B, C sao cho \(\overrightarrow {CA} \) và \(\overrightarrow {CB} \) ngược hướng 

Hình vẽ nào trong các hình vẽ bên là đúng?

A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Câu 8: Cho tam giác ABC. Mệnh đề nào sau đây là đúng?

A. Với mọi điểm E trên đường thẳng BC, vectơ \(\overrightarrow {AE} \) không cùng phương với vectơ \(\overrightarrow {BC} \).

B. Vectơ \(\overrightarrow {AE} \) có thể cùng phương với vectơ \(\overrightarrow {BC} \).

C. Tập hợp các điểm M sao cho \(\overrightarrow {AM} \) cùng phương với \(\overrightarrow {BC} \) là một đường thẳng qua A.

D. Tập hợp các điểm N sao cho \(\overrightarrow {AN} \) cùng hướng với \(\overrightarrow {BC} \) là đường thẳng qua A, song song với BC.

Câu 9: Cho 4 điểm A, B, C, D thỏa mãn điều kiện \(\overrightarrow {AB}  = \overrightarrow {DC} \). Khẳng định nào sau đây là đúng?

A. ABCD là hình bình hành

B. \(\overrightarrow {AD}  = \overrightarrow {CB} \)

C. \(\overrightarrow {CB}  = \overrightarrow {BD} \)

D. ABCD là hình bình hành nếu trong 4 điểm A, B, C, D không có ba điểm nào thẳng hàng.

Câu 10: Khẳng định nào sau đây sai?

A. Vectơ – không là vectơ có phương tùy ý.

B. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương với nhau.

C. Hai vectơ cùng phương với một vectơ thứ ba khác 0→ thì cùng phương với nhau.

D. Điều kiện cần để hai vectơ bằng nhau là chúng có độ dài bằng nhau.

Bài học này chúng ta sẽ bắt đầu với khái niệm vectơ, một khái niệm hoàn toàn mới. Đây là khái niệm cơ bản và nền tảng, làm cơ sở cho Hình học của cả lớp 10, 11, 12.