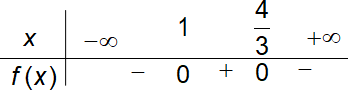Toán 10 Chương 4 Bài 5: Dấu của tam thức bậc hai
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Dấu của tam thức bậc hai. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Định lí về dấu của tam thức bậc hai
- Định nghĩa: Tam thức bậc hai đối với là biểu thức có dạng \(f(x) = a{x^2} + bx + c,\) trong đó \(a,b,c\) là những hệ số \(,a \ne 0.\)
Ví dụ 1:
a.\(f(x) = {x^2} +2x+3\) là tam thức bậc hai với \(a=1 \ne 0, b=2,c=3 \)
b.\(f(x) = x^2-1\) là tam thức bậc hai với \(a=1 \ne 0, b=0, c=-1\)
Chú ý: Nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) cũng là nghiệm của tam thức bậc hai \(f(x) = a{x^2} + bx + c,\Delta = {b^2} - 4ac\;(\Delta ' = b{'^2} - ac)\) được gọi là biệt thức(biệt thức thu gọn ) của tam thức bậc hai.
- Định lý về Dấu của tam thức bậc hai
Cho \(f(x) = a{x^2} + bx + c,\Delta = {b^2} - 4ac\)
- Nếu \(\Delta < 0\) thì f(x) luôn cùng dấu với hệ số a với mọi \(x \in R\)
- Nếu \(\Delta = 0\) thì f(x) luôn cùng dấu với hệ số a trừ khi \(x = - \frac{b}{{2a}}\)
- Nếu \(\Delta > 0\) thì f(x) cùng dấu với hệ số a khi \(x < {x_1}\) hoặc \(x > {x_2}\) trái dấu với hệ số a khi \({x_1} < x < {x_2}\) trong đó \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\) là hai nghiệm của f(x)
Các kết quả trên được thể hiện qua các bảng sau:
- Với \(\Delta < 0\)
- Với \(\Delta = 0\)
- Với \(\Delta > 0\)
- Cách xét dấu tam thức bậc hai
- Tìm nghiệm tam thức (bấm máy)
- Lập bảng xét dấu dựa vào dấu của hệ số a.
- Dựa vào bảng xét dấu và kết luận.
1.2. Bất phương trình bậc hai một ẩn
- Định nghĩa: Bất phương trình bậc hai ẩn x là bất phương trình dạng \(a{x^2} + bx + c < 0\) (hoặc
\(a{x^2} + bx + c \le 0,a{x^2} + bx + c > 0,a{x^2} + bx + c \ge 0\)), trong đó \(a,b,c\) là những số thực đã cho \(,a \ne 0.\).
Ví dụ 2: \({3x^2} +2 < 0;3{x^2} - 6x + 3 > 0\)
- Giải bất phương trình bậc hai
Giải bất phương trình bậc hai \(a{x^2} + bx + c < 0\) thực chất là tìm các khoảng mà trong đó \(f(x) = a{x^2} + bx + c\) cùng dấu với hệ số a ( trường hợp a < 0) hay trái dấu với hệ số a ( trường hợp a > 0)
2. Bài tập minh họa
Câu 1:
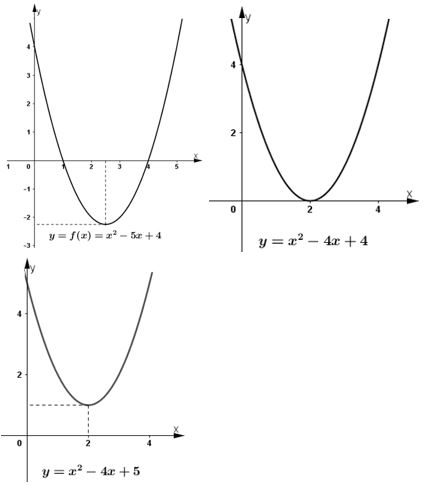
a) Xét tam thức bậc hai f(x) = x2 – 5x + 4. Tính f(4), f(2), f(-1), f(0) và nhận xét về dấu của chúng.
b) Quan sát đồ thị hàm số y = x2 – 5x + 4 (h.32a)) và chỉ ra các khoảng trên đó đồ thị ở phía trên, phía dưới trục hoành.
c) Quan sát các đồ thị trong hình 32 và rút ra mối liện hệ về dấu của giá trị f(x) = ax2 + bx + c ứng với x tùy theo dấu của biệt thức Δ = b2 – 4ac
Hướng dẫn giải
Xét f(x) = x2 – 5x +4
\(\begin{array}{l}
f\left( 4 \right) = {4^2} - 5.4 + 4 = 0\\
f\left( 2 \right) = {2^2} - 5.2 + 4 = - 2 < 0\\
f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 5.\left( { - 1} \right) + 4 = 10 > 0\\
f\left( 0 \right) = {0^2} - 5.0 + 4 = 4 > 0
\end{array}\)
Câu 2: Xét dấu các tam thức: f(x) = 3x2 + 2x – 5;
Hướng dẫn giải
f(x) = 3x2 + 2x – 5 có hai nghiệm phân biệt x = 1; x = -5/3, hệ số a = 3 >0.
Ta có bảng xét dấu f(x) như sau:
Câu 3: Giải bất phương trình \( - 3{x^2} + 7x - 4 < 0\)
Hướng dẫn giải:
Ta đặt \(f(x) = - 3{x^2} + 7x - 4\)
\({ - 3{x^2} + 7x - 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{x = \frac{4}{3}}
\end{array}} \right.}\)
Hệ số a = -3 < 0
Bảng xét dấu
Vậy tập nghiệm của bất phương trình là \(T = \left( { - \infty ;1} \right) \cup \left( {\frac{4}{3}; + \infty } \right).\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Xét dấu tam thức \(f(x) = 4{x^2} + 3x - 7.\)
Câu 2: Xét dấu biểu thức \(f(x) = \frac{{{4x^2} + 4x + 1}}{{{x^2} - 9}}\)
Câu 3: Giải bất phương trình \( - 4{x^2} + 9x - 5 < 0\)
3.2. Bài tập trắc nghiệm
Câu 1: Để bất phương trình \(\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\) nghiệm đúng \(\forall x \in \left[ { - 5;3} \right]\), tham số a phải thỏa điều kiện:
A. \(a \ge 3\)
B. \(a \ge 4\)
C. \(a \ge 5\)
D. \(a \ge 6\)
Câu 2: Với giá trị nào của m thìphương trình \(\sqrt {{x^2} - 2m} + 2\sqrt {{x^2} - 1} = x\) vô nghiệm?
A. \(m \le \frac{2}{3}\)
B. \(\left[ \begin{array}{l} m < 0\\ m > \frac{2}{3} \end{array} \right.\)
C. \(0 \le m \le \frac{2}{3}\)
D. m = 0
Câu 3: Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}} {{x^2} - 3x - 4 \le 0}\\ {{x^3} - 3\left| x \right|x - {m^2} + 6m \ge 0} \end{array}} \right.\). Để hệ có nghiệm, các giá trị thích hợp của tham số m là:
A. \(2 \le m \le 8\;\)
B. \(-8 \le m \le 2\;\)
C. \(-2 \le m \le 8\;\)
D. \(-8 \le m \le -2\;\)
Câu 4: Hệ bất phương trình: \(\left\{ \begin{array}{l} {x^2} - 5x + 4 \le 0\\ {x^2} - ({m^2} + 3)x + 2({m^2} + 1) \le 0 \end{array} \right.\) có tập nghiệm biểu diễn trên trục số có độ dài bằng 1, với giá trị của m là:
A. m = 0
B. \(m = \sqrt 2 \)
C. \(m = -\sqrt 2 \)
D. Tất cả đều đúng
3.3. Trắc nghiệm Online
4. Kết luận
Qua bài học này, các em cần nắm được các nội dung sau:
- Khái niệm cơ bản về Dấu của tam thức bậc hai.
- Phương pháp để giải bất phương trình bất phương trình bậc hai một ẩn.