Toán 10 Chương 3 Bài 2: Phương trình đường tròn

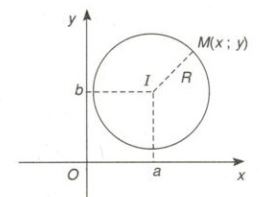
Trong mặt phẳng Oxy cho đường tròn (C) tâm I(a;b) bán kính R.

Ta có \(M\left( {x;y} \right) \subset \left( C \right) \Leftrightarrow IM = R\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} = R\\ \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2} \end{array}\)

Vì vậy, phương trình \({{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} = {R^2}}\) được gọi là phương trình đường tròn tâm I(a;b) bán kính R

Chú ý: Phương trình đường tròn có tâm là gốc tọa độ O và có bán kính R là: 

\(x^2+x^2=R^2\)

Phương trình đường tròn \({{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} = {R^2}}\) có thể viết lại dưới dạng \({x^2} + {y^2} - 2{\rm{ax}} - 2by + c = 0\) trong đó \(c=a^2+b^2-R^2\).

Ngược lại, phương trình \({x^2} + {y^2} - 2{\rm{ax}} - 2by + c = 0\) là phương trình của đường tròn (C) khi và chỉ khi \({a^2} + {b^2} - c > 0\). Khi đó đường tròn (C) có tâm I(a;b) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} \)

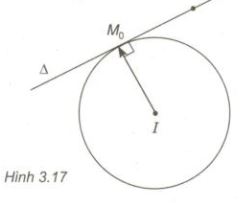
Cho điểm \(M_0\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn tâm I(a;b). Gọi \(\Delta\) là tiếp tuyến của (C) tại \(M_0\)

Ta có \(M_0\) thuộc \(\Delta\) và vectơ \(\overrightarrow {I{M_0}} = \left( {{x_0} - a;{y_0} - b} \right)\) là vectơ pháp tuyến của \(\Delta\). Do đó, \(\Delta\) có phương trình là 

\(\left( {{x_0} - a} \right)\left( {x - {x_0}} \right) + \left( {{y_0} - b} \right)\left( {y - {y_0}} \right) = 0\)

Đây chính là phương trình tiếp tuyến của đường tròn \({{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} = {R^2}}\) tại điểm \(M_0\) trên đường tròn.

Câu 1: Tìm tâm và bán kính của các đường tròn sau:

a) \({x^2} + {y^2} + 8{\rm{x}} - 6y + 16 = 0\)

b) \(4{x^2} + 4{y^2} + 5{\rm{x}} - 16y + 10 = 0\)

Hướng dẫn giải

a)

\(\begin{array}{l} {x^2} + {y^2} + 8{\rm{x}} - 6y + 16 = 0\\ \Leftrightarrow {x^2} + 8{\rm{x}} + 16 + {y^2} - 6y + 9 = 9\\ \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^2} = {3^2} \end{array}\)

Nên đường tròn có tâm I(-4;3) và bán kính R = 3.

b)

 \(\begin{array}{l} 4{x^2} + 4{y^2} + 5{\rm{x}} - 16y + 10 = 0\\ \Leftrightarrow {x^2} + {y^2} + \frac{{5{\rm{x}}}}{4} - 4y + \frac{5}{2} = 0\\ \Leftrightarrow {x^2} + 2.x.\frac{5}{8} + \frac{{25}}{{64}} + {y^2} - 4y + 4 = \frac{{121}}{{64}}\\ \Leftrightarrow {\left( {x + \frac{5}{8}} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {\frac{{11}}{8}} \right)^2} \end{array}\)

Nên đường tròn có tâm \(I\left( {\frac{{ - 5}}{8};2} \right)\) và bán kính \(R = \frac{{11}}{8}\)

Câu 2: Viết phương trình đường tròn đi qua 3 điểm: A(1;2), B(3;4) C(1;6)

Hướng dẫn giải

Tâm I của đường tròn này là giao điểm của đường trung trực của AB và BC.

Phương trình đường trung trực  AB: x + y - 5 = 0

Phương trình đường trung trực BC: x - y + 3 = 0

Nên tâm I (1;4) và R = 2

Vậy phương trình đường tròn: (C): \({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} = 4\)

Câu 1: Tìm tâm và bán kính của các đường tròn sau:

a) \(x^2+ y^2- 4x -4y - 1 = 0\)

b) \(4x^2+ 9y^2+ 4x - 12y - 11 = 0\)

c) \(x^2 + y^2 - 6x + 4y - 3 = 0\)

Câu 2: Lập phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(-1; 4) và đi qua M(1; -2);

b) (C) có tâm I(2; -1) và tiếp xúc với đường  thẳng \(d : x - y + 3 = 0\)

c) (C) có đường kính AB với A(2; 3) và B(6; 6)

Câu 3: Lập phương trình đường tròn đi qua ba điểm: A(1; 2); B(3; 4); C(4; -3)

Câu 1: Cho đường tròn (C) có phương trình x²+y²+2x-8y=0. Khi đó đường tròn có tâm I và bán kính R với

A. I(2;-8), R=2√2

B. I(1;-4), R=3

C.  I(-1;4), R=3

D. I(1;-4), R=2√2

Câu 2: Phương trình đường tròn đi qua ba điểm A(-1; 3), B(1; 4), C(3; 2) là:

A. \({x^2} + {y^2} - \frac{5}{3}x - \frac{{11}}{3}y + \frac{2}{3} = 0\)

B. \({x^2} + {y^2} - \frac{5}{2}x - \frac{{11}}{3}y - \frac{2}{3} = 0\)

C. \({x^2} + {y^2} - \frac{5}{6}x - \frac{{11}}{6}y - \frac{2}{3} = 0\)

D. \({x^2} + {y^2} - \frac{5}{6}x - \frac{{11}}{6}y + \frac{2}{3} = 0\)

Câu 3: Cho đường tròn (C) có phương trình x²+y²-6x+4y-12=0. Phương trình tiếp tuyến của đường tròn tại điểm A(-1; 1) là:

A. – 4x + 3y – 7 = 0

B. 4x + 3y + 1= 0

C.  3x + 4y – 1 = 0

D. 3x – 4y + 7 = 0

Câu 4: Cho đường tròn (C) có tâm I(2; 5) và tiếp xúc với đường thẳng Δ: 3x – 4y – 6 = 0. Khi đó (C) có bán kính là:

A. R=2

B. R=2√2

C. R=3

D. R=4

Câu 5:  Đường tròn có tâm nằm trên đường thẳng Δ: x + 2y – 6 = 0 và tiếp xúc với hai trục tọa độ. Khi đó bán kính của đường tròn là

A. R = 2 hoặc R = 4

B.  R = 2 hoặc R = 6

C. R = 3 hoặc R = 6

D.  R = 3 hoặc R = 4

Qua bài học này, các em cần nắm được những nội dung sau:

• Phương pháp để lập phương trình của một đường tròn.
• Làm được các dạng toán liên quan đến đường tròn.