Toán 10 Ôn tập chương 5 Thống kê

• Dấu hiệu là một vấn đề mà người điều tả quan tâm.
• Đơn vị điều tra là mỗi đối tượng điều tả.
• Mẫu là một tập hợp con hữu hạn các đơn vị điều tra.
• Kích thước mẫu là số phần tử của mẫu.
• Mẫu số liệu là giá trị của dấu hiệu thu được trên mẫu.
• Trình bày một mẫu số liệu có 2 cách chính: dạng bảng và dạng biểu đồ.

- Số trung bình cộng (ký hiệu \(\overline x \)): 

\(\bar x = \frac{1}{n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}) = {f_1}{x_1} + {f_2}{x_2} + ... + {f_k}{x_k}\)

hoặc \(\bar x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) = {f_1}{c_1} + {f_2}{c_2} + ... + {f_k}{c_k}\)

- Số trung vị (ký hiệu M_e): Cho mẫu số liệu có kích thước n được sắp xếp theo thứ tự không giảm (hoặc không tăng)

• Nếu n lẻ thì M_e là số đứng chính giữa dãy ( số hạng thứ \(\frac{{n + 1}}{2}\)).
• Nếu n chẵn thì M_e là  trung bình cộng của 2 số đứng giữa dãy (số hạng thứ \(\frac{n}{2}\) và số hạng thứ \(\frac{n}{2} + 1\)).

- Mốt (ký hiệu \(M_0\)): Giá trị có tần số lớn nhất.

- Phương sai (ký hiệu s²):

\(\begin{array}{l}
{s^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{x_k} - \overline x } \right)}^2}} \right]\\
 = {f_1}{\left( {{x_1} - \overline x } \right)^2} + {f_2}{\left( {{x_2} - \overline x } \right)^2} + ... + {f_k}{\left( {{x_k} - \overline x } \right)^2}
\end{array}\)

hoặc

\(\begin{array}{l}
{s^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\
 = {f_1}{\left( {{c_1} - \overline x } \right)^2} + {f_2}{\left( {{c_2} - \overline x } \right)^2} + ... + {f_k}{\left( {{c_k} - \overline x } \right)^2}
\end{array}\)

- Độ lệch chuẩn (ký hiệu s): \(s = \sqrt {{s^2}} \)

Câu 1: Điểm trung bình các môn học của học sinh được cho trong bảng sau:

a) Hãy tính điểm trung bình của học sinh? (không được áp dụng công

thức \(\bar x = \frac{1}{n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k})\)

b) Hãy tính phương sai và độ lệch chuẩn của bảng phân bố tần số, tần suất trên.

Hướng dẫn giải

a) Điểm trung bình của học sinh là:

\(\begin{array}{*{20}{l}}
{\bar x = {f_1}{x_1} + {f_2}{x_2} + {f_3}{x_3} + {f_4}{x_4} + {f_5}{x_5} + {f_6}{x_6}}\\
{ = \frac{{9,09}}{{100}}.7,5 + \frac{{18,18}}{{100}}.7,8 + \frac{{27,27}}{{100}}.8,0 + \frac{{18,18}}{{100}}.8,4 + \frac{{18,18}}{{100}}.9,0 + \frac{{9,09}}{{100}}.9,5}\\
{ \approx 8,3}
\end{array}\)

b) Phương sai s²

 \(\begin{array}{l}
\begin{array}{*{20}{l}}
{{s^2} = {f_1}{{\left( {{x_1} - \bar x} \right)}^2} + {f_2}{{\left( {{x_2} - \bar x} \right)}^2} + ... + {f_k}{{\left( {{x_k} - \bar x} \right)}^2}}
\end{array}\\
 = \frac{{9,09}}{{100}}{\left( {7,5 - 8,3} \right)^2} + \frac{{18,18}}{{100}}{\left( {7,8 - 8,3} \right)^2} + \frac{{27,27}}{{100}}{\left( {8,0 - 8,3} \right)^2}\\
 + \frac{{18,18}}{{100}}{\left( {8,4 - 8,3} \right)^2} + \frac{{18,18}}{{100}}{\left( {9,0 - 8,3} \right)^2} + \frac{{9,09}}{{100}}{\left( {9,5 - 8,3} \right)^2}\\
 \approx 0,35
\end{array}\)

Độ lệch chuẩn

 \(s = \sqrt {{s^2}}  \approx 0,59\)

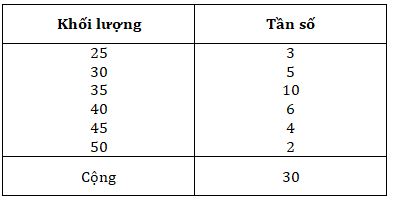
Câu 2: Cho bảng phân bố tần số khối lượng 30 quả trứng gà của một ổ trứng gà:

a) Tính số trung bình, số trung vị, mốt

b) Hãy chọn giá trị đại diện cho các số liệu thống kê đã cho về quy mô và độ lớn

c) Giả sử có rổ trứng gà thứ hai có \(\overline {{x_2}}  = 36,5\)g, \({s_2} = 10\)g, hãy xét xem trứng gà ở rổ nào có  khối lượng đều hơn.

Hướng dẫn giải

a) Số trung bình cộng:

\(\overline x  = \) (25.3+30.5+35.10+40.6+45.4+50.2)/30 = 36,5 g

Số trung vị: \({M_e} = 35g;\)

Mốt: \({M_0} = 35g\)

b)Ta chọn số trung bình  = 36,5 g để làm giá trị đại diện cho các số liệu thống kê đã cho ở quy mô và độ lớn.

c) Phương sai:

Độ lệch chuẩn \({s_1} = \sqrt {s_1^2}  = 6,73\)

Rổ trứng thứ nhất và rổ trứng thứ hai có cùng đơn vị đo và \(\overline {{x_1}}  = \overline {{x_2}}  = 36,5g;{s_1} = 6,73g < 10g = {s_2}\). Suy ra trứng gà ở rổ thứ nhất đồng đều hơn.

Câu 1: 400 quả trứng được phân thành năm lớp căn cứ trên khối lượng (đơn vị gam) của chúng. Ta có bảng phân bố tần số ghép lớp:

a) Tính số trung bình.

b) Tính phương sai và độ lệch chuẩn.

Câu 2: Một người lái xe thường xuyên đi lại giữa hai điểm A và B thời gian đi (tính bằng phút) được ghi lại trong bảng phân bố tần số sau:

a) Tính thời gian trung bình mà người đó đi từ A đến B.

b) Tính phương sai và độ lệc chuẩn

Câu 1: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là:

A. Tần suất 

B. Số trung bình 

C. Số trung vị 

D. Mốt 

Câu 2: Tỉ số giữa tần số và số các số liệu thống kê được gọi là:

A. Tần suất 

B. Mốt 

C. Phương sai 

D. Số trung bình 

Câu 3:  Số lần xuất hiện của một giá trị trong mẫu số liệu thống kê được gọi là:

A. Tần suất 

B. Tần số 

C. Số trung vị 

D. Mốt 

Câu 4: Đại lượng đo mức độ biến động, chênh lệch giữa các giá trị trong mẫu số liệu thống kê gọi là:

A. Độ lệch chuẩn 

B. Phương sai 

C. Số trung vị 

D. Tần số 

Câu 5: Điểm thi học kỳ của một học sinh như sau:

4    6    2    7    3    5    9    8    7    9    10

Số trung bình và số trung vị lần lượt là:

A. 6,22 và 7

B. 6,36 và 7

C. 7 và 6

D. 6 và 6

Qua bài học này, các em cần nắm được những nội dung sau:

• Khái quát được nội dung phần Thống kê đã được học.
• Làm được các bài tập của chương.