Toán 10 Chương 1 Bài 3: Tích của vectơ với một số
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Tích của vectơ với một số. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Định nghĩa tích của một vectơ và một số
Tích của vectơ \(\vec{a}\) với số thực k là một vectơ, kí hiệu là \(k\vec{a}\), được xác định như sau:
-
Nếu \(k\geq 0\) thì vectơ \(k\vec{a}\) cùng hướng với vectơ \(\vec{a}\).
-
Nếu \(k<0\) thì vectơ \(k\vec{a}\) ngược hướng với vectơ \(\vec{a}\).
-
Độ dài của vectơ \(k\vec{a}\) bằng \(|k|.|\vec{a}|\).
1.2. Các tính chất của phép nhân vectơ với số
Với hai vectơ bất kì \(\vec{a}\), \(\vec{b}\) và mọi số thực k, l ta có:
- \(k\left( {l\overrightarrow a } \right) = \left( {kl} \right)\overrightarrow a\)
- \(\left( {k + l} \right)\overrightarrow a = k\overrightarrow a + l\overrightarrow a \)
- \(k\left( {\overrightarrow a + \overrightarrow b } \right) = k\overrightarrow a + k\overrightarrow b ;\,\,\,k\left( {\overrightarrow a - \overrightarrow b } \right) = k\overrightarrow a - k\overrightarrow b \)
- \(k\overrightarrow a = \overrightarrow 0 \) khi và chỉ khi \(k = 0\) hoặc \(\vec{a} =\vec{0}\).
1.3. Điều kiện để hai vectơ cùng phương
Vectơ \(\vec{b}\) cùng phương với vectơ \(\vec{a}\neq \vec{0}\) khi và chỉ khi tồn tại số k sao cho \(\vec{b}=k\vec{a}\)
Ứng dụng vào ba điểm thẳng hàng:
Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là có số k sao cho \(\vec{AB}=k\vec{AC}\)
1.4. Biểu thị một vectơ qua hai vectơ không cùng phương
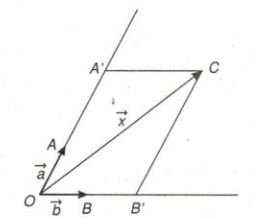
Dựa vào hình trên, ta có định lí sau:
Cho hai vectơ không cùng phương \(\vec{a}\) và \(\vec{b}\). Khi đó mọi vectơ \(\vec{x}\) đều có thể hiển thị một cách duy nhất qua hai vectơ \(\vec{a}\) và \(\vec{b}\), nghĩa là có cặp số duy nhất m và n sao cho:
\(\vec{x}=m\vec{a}+n\vec{b}\)
2. Bài tập minh họa
Câu 1: Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \) . Xác định độ dài và hướng của vectơ \(\overrightarrow a + \overrightarrow a\)
Hướng dẫn giải
Ta có:
\(\overrightarrow a + \overrightarrow a = 2\overrightarrow a \)
Độ dài của vecto \(\overrightarrow a + \overrightarrow a\) bằng 2 lần độ dài của vecto \(\overrightarrow a\)
Hướng của vecto \(\overrightarrow a + \overrightarrow a\) cùng hướng với vecto \(\overrightarrow a\) (vì 2 > 0).
Câu 2: Tìm vectơ đối của các vectơ: \(k\overrightarrow a ;\,\,3\overrightarrow a - 4\overrightarrow b \)
Hướng dẫn giải
Vectơ đối của các vectơ \(k\overrightarrow a \) là vectơ -\(k\overrightarrow a \)
Vectơ đối của các vectơ \(3\overrightarrow a - 4\overrightarrow b \) là vectơ -(\(3\overrightarrow a - 4\overrightarrow b \)) hay \( - 3\overrightarrow a + 4\overrightarrow b \).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác OAB vuông cân với \(OA = OB = a\) . Tính độ dài của các vectơ \(\overrightarrow {AO} + \overrightarrow {OB} + \overrightarrow {AB} ;\) \(3\overrightarrow {OA} - 2\overrightarrow {OB} \)
Câu 2: Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có hệ thức: \(\overrightarrow {BA} - \overrightarrow {BC} = \overrightarrow {DA} - \overrightarrow {DC} \) .
Câu 3: Cho tam giác ABC. M là trung điểm của BC. Chứng minh rằng: \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 2MC. Khi đó khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
B. \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
C. \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AC} \)
D. \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
Câu 2: Cho tứ giác ABCD; X là trọng tâm của tam giác BCD, G là trọng tâm tứ giác ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {GA} + \overrightarrow {GX} = \overrightarrow 0 \)
B. \(\overrightarrow {GA} +3 \overrightarrow {GX} = \overrightarrow 0 \)
C. \(\overrightarrow {GB} + \overrightarrow {GX} = \overrightarrow 0 \)
D. \(\overrightarrow {GC} + \overrightarrow {GX} = \overrightarrow 0 \)
Câu 3: Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?
A. \(a\overrightarrow {GA} + b\overrightarrow {GB} + c\overrightarrow {GC} = \overrightarrow 0 \)
B. \(a\overrightarrow {GA} + b\overrightarrow {GB} - c\overrightarrow {GC} = \overrightarrow 0 \)
C. \(a\overrightarrow {GA} - b\overrightarrow {GB} + c\overrightarrow {GC} = \overrightarrow 0 \)
D. \( - a\overrightarrow {GA} + b\overrightarrow {GB} + c\overrightarrow {GC} = \overrightarrow 0 \)
Câu 4: Tìm khẳng định sai:
A. Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương
B. Hai vectơ cùng hướng với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương
C. Ba vectơ \(\vec{a},\vec{b},\vec{c}\) khác \(\vec{0}\) đôi một cùng phương thì ít nhất có hai vectơ cùng phương
D. Để \(\vec{a}\) và \(\vec{b}\) bằng nhau thì \(|\vec{a}|=|\vec{b}|\)
Câu 5: Cho vectơ \(\overrightarrow a ,\overrightarrow b \) và các số thực m, n, k. Khẳng định nào sau đây là đúng?
A. Từ đẳng thức \(m\vec {a} = n\vec {b} \) suy ra m = n
B. Từ đẳng thức \(k\vec {a} = k\vec {kb} \) luôn suy ra \(\vec a = \vec b \)
C. Từ đẳng thức \(k\vec {a} = k\vec {kb} \) luôn suy ra k = 0
D. Từ đẳng thức \(m\vec {a} = n\vec {b} \) và \(\vec a \ne \vec 0\) suy ra m = n
Câu 6: Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \). Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?
A. k < 0
B. k = 1
C. 0 < k < 1
D. k > 1
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Tích của vectơ với một số Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Định nghĩa tính chất tích của một vectơ với một số.
- Nhận biết hai vectơ cùng phương.
- Cách biểu thị một vectơ theo hai vectơ không cùng phương.