Toán 10 chương 3 Bài 3: Phương trình đường elip
Mời các em cùng tham khảo nội dung bài giảng Phương trình đường elip do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Định nghĩa đường elip
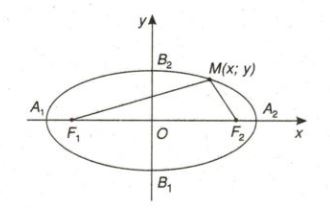
Cho hai điểm cố định F1, F2 và một độ dài không đổi 2a lớn hơn F1F2. Elip là tập hợp các điểm M trong mặt phẳng sao cho
F1M+F2M=2a
Các điểm F1 và F2 gọi là các tiêu điểm của elip. Độ dài F1F2 gọi là tiêu cự của elip.
1.2. Phương trình chính tắc của elip
Cho elip (E) có các tiêu điểm F1 và F2. Điểm M thuộc elip khi và chỉ khi F1M+F2M=2a. Chọn hệ trục tọa độ Oxy sao cho F1=(-c;0) và F2=(c;0). Khi đó phương trình chính tắc của elip là:
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
trong đó b2 = a2 - c2
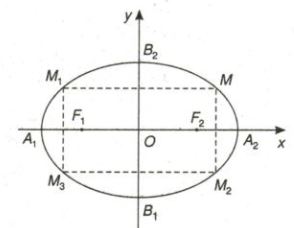
1.3. Hình dạng của elip
- (E) có trục đối xứng là Ox, Oy và có tâm đối xứng là O
- Các điểm A1, A2, B1, B2 gọi là các đỉnh của elip
- Đoạn thẳng A1A2 gọi là trục lớn, đoạn thẳng B1B2 gọi là trục nhỏ của elip.
1.4. Liên hệ giữa đường tròn và đường elip
- Từ hệ thức b2 = a2 - c2 ta thấy nếu tiêu cự càng nhỏ thì b càng gần a, tức là trục nhỏ của elip càng gần trục lớn. Lúc đó elip có dạng gần như đường tròn.
- Cho đường tròn (C) có phương trình \({x^2} + {y^2} = {a^2}\). Với mỗi điểm M(x;y) thuộc đường tròn, xét điểm M'(x';y') sao cho \(\left\{ \begin{array}{l} x' = x\\ y' = \frac{b}{a}y \end{array} \right.\left( {0 < b < a} \right)\)
thì tập hợp các điểm M' có tọa độ thỏa phương trình \(\frac{{{x'^2}}}{{{a^2}}} + \frac{{{y'^2}}}{{{b^2}}} = 1\) là một elip (E)
Ta nói đường tròn (C) được co thành elip (E).
2. Bài tập minh họa
Câu 1: Xác định độ dài các trục, tọa độ các tiêu điểm, tọa độ các đỉnh của elip có phương trình
\(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
Hướng dẫn giải
Ta có a2 = 9⇒ a = 3, b2 = 1 ⇒ b = 1
Vậy c2 = a2 - b2 = 9 - 1 = 8 ⇒ c = \(2\sqrt 2 \)
Độ dài trục lớn là A1A2 = 2a = 6
Độ dài trục nhỏ là: B1B2 = 2b = 2
Tiêu điểm là: \({F_1}\left( { - 2\sqrt 2 ;0} \right),{F_2}\left( {2\sqrt 2 ;0} \right)\)
Tọa độ các đỉnh là \({A_1}\left( { - 3;0} \right),{A_2}\left( {3;0} \right),{B_1}\left( {0; - 1} \right),{B_2}\left( {0;1} \right)\)
Câu 2: Lập phương trình chính tắc của elip, biết:
a) (E) đi qua điểm \(M\left( {\frac{3}{{\sqrt 5 }};\frac{4}{{\sqrt 5 }}} \right)\) và M nhìn hai tiêu điểm \({F_1},{F_2}\) dưới một góc vuông.
b) (E) đi qua \(M\left( {\sqrt 3 ;\frac{{\sqrt 6 }}{2}} \right)\) và một tiêu điểm F nhìn trục nhỏ dưới góc 60o.
Hướng dẫn giải
a) Do (E) đi qua M nên \(\frac{9}{{5{a^2}}} + \frac{{16}}{{5{b^2}}} = 1\) (1); Lại có \({\widehat {{F_1}MF}_2} = {90^0} \Leftrightarrow OM = \frac{1}{2}{F_1}{F_2} = c \Leftrightarrow c = \sqrt 5 \)
Như vậy ta có hệ điều kiện \(\left\{ \begin{array}{l}
\frac{9}{{5{a^2}}} + \frac{{16}}{{5{b^2}}} = 1\\
{a^2} - {b^2} = 5
\end{array} \right.\). Giải hệ ta được \({a^2} = 9;{b^2} = 4 \Rightarrow (E):\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
b) Tiêu điểm F nhìn trục nhỏ dưới góc 60o nên tam giác FB1B2 đều (B1, B2 là hai đỉnh trên trục nhỏ), suy ra \(c = b\sqrt 3 \Rightarrow a = 2b\), từ đó tìm ra \((E):\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{\frac{9}{4}}} = 1\)
Câu 3: Cho elip \((E):\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\). Tìm điểm \(M \in (E)\) sao cho \(M{F_1} = 2M{F_2}\).
Hướng dẫn giải
Gọi \(M(x;y) \Rightarrow M{F_1} = 2 + \frac{{\sqrt 3 }}{2}x;M{F_2} = 2 - \frac{{\sqrt 3 }}{2}x\). Từ \(M{F_1} = 2M{F_2} \Rightarrow x = \frac{4}{{3\sqrt 3 }}\)
Từ đó tìm ra \(y = \pm \frac{{\sqrt {23} }}{{3\sqrt 3 }}\). Vậy có hai điểm M cần tìm là \(M\left( {\frac{4}{{3\sqrt 3 }}; \pm \frac{{\sqrt {23} }}{{3\sqrt 3 }}} \right)\).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Xác đinh độ dài các trục, tọa độ tiêu điểm, tọa độ các đỉnh và vẽ các elip có phương trình sau:
a) \(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\)
b) \(9x^2 + 4y^2 = 1\)
c) \(25x^2 + 4y^2 = 9\)
Câu 2: Lập phương trình chính tắc của elip, biết:
a) Trục lớn và trục nhỏ lần lươt là 12 và 9
b) Trục lớn bằng 15 và tiêu cự bằng 12
Câu 3: Lập phương trình chính tắc của elip trong các trường hợp sau:
a) Elip đi qua các điểm M(-1;2) và \(N(1;-\frac{7}{3})\)
b) Elip có một tiêu điểm là \(F_1(\sqrt{2};0)\) và điểm \(M(2;\frac{\sqrt{4}}{3})\) nằm trên elip.
3.2. Bài tập trắc nghiệm
Câu 1: Phương trình chính tắc của elip có độ dài trục lơn bằng 8, độ dài trục nhỏ bằng 6 là:
A. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{36} = 1\)
B. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{{9}} + \frac{{{y^2}}}{16} = 1\)
D. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Câu 2: Phương trình của elip có 1 tiêu điểm F2(1;0) và đi qua điểm M(2; -2/√5) là:
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)
B. 4x2+5y2=1
C. \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\)
D. 5x2+4y2=1
Câu 3: Cho elip có phương trình 4x2+9y2=36. Khi đó hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 12
C. 24
D. 36
Câu 4: Cho elip (E) có phương trình
\(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\)
Đường thẳng nào sau đây cắt (E) tại hai điểm đối xứng nhau qua trục Oy?
A. y=2x
B. y=3
C. x=3
D. y=10
Câu 5: Cho elip (E) có phương trình
\(\frac{{{x^2}}}{{169}} + \frac{{{y^2}}}{{25}} = 1\)
với hai tiêu điểm là F1,F2. Với điểm M bất kì trên (E) thì chu vi tam giác MF1F2là:
A. 50
B. 36
C. 34
D. Thay đổi phụ thuộc vào vị trí M
3.3. Trắc nghiệm Online
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Những nội dung cơ bản nhất về Phương trình đường elip
- Phương pháp giải các dạng toán liên quan đến đường elip.