Toán 10 Ôn tập Chương 3: Phương pháp tọa độ trong mặt phẳng

Trong mặt phẳng Oxy, cho đường thẳng \(\Delta\) đi qua M0(x0;y0) và có VTCP \(\overrightarrow u  = \left( {{u_1};{u_2}} \right)\). Phương trình tham số của \(\Delta\):

\(\left\{ \begin{array}{l}
x = {x_0} + t{u_1}\\
y = {y_0} + t{u_2}
\end{array} \right.\)

Trong mặt phẳng Oxy, cho đường thẳng \(\Delta\) đi qua M0(x0;y0) và nhận làm vectơ pháp tuyến thì phương trình tổng quát của \(\Delta\) là:

\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

\({\rm{cos}}\widehat {\left( {{\Delta _1},{\Delta _2}} \right)} = c{\rm{os}}\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}\)

\(d\left( {{M_0},\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Trong mặt phẳng Oxy cho đường tròn (C) tâm I(a;b) bán kính R. Phương trình chính tắc của đường tròn (C) là:

\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

Câu 1: Cho tam giác ABC, biết phương trình ba cạnh của tam giác là

AB: x – 3y – 1 = 0, BC: x + 3y + 7 = 0, CA: 5x – 2y + 1 = 0

Hãy viết phương trình đường cao AH của tam giác ABC

Hướng dẫn giải

Tọa độ đỉnh A là nghiệm của hệ phương trình

\(\left\{ \begin{array}{l}
x - 3y - 1 = 0\\
5x - 2y + 1 = 0
\end{array} \right. \Rightarrow A\left( { - \frac{5}{{13}}; - \frac{6}{{13}}} \right)\)

Vì \(AH \bot BC\) nên đường thẳng AH có VTPT là \(\overrightarrow {{u_{BC}}}  = \left( {3; - 1} \right)\)

Do đó phương trình đường cao AH của tam giác ABC là:

\(3\left( {x + \frac{5}{{13}}} \right) - \left( {y + \frac{6}{{13}}} \right) = 0 \Leftrightarrow 39x - 13y + 9 = 0\)

Câu 2: Cho hình chữ nhật ABCD có đỉnh A(7; 4) và phương trình hai cạnh: 7x – 3y + 5 = 0, 3x + 7y – 1 = 0. 

Tính diện tích hình chữ nhật ABCD.

Hướng dẫn giải

Ta kiểm tra thấy đỉnh A(7; 4) không nằm trên các đường thẳng d1: 7x-3y+5=0, d2: 3x+7y-1=0 nên đây là các cạnh CB, CD. Ta có

\(\begin{array}{l}
{S_{ABCD}} = AB.AD = d\left( {A,BC} \right).d\left( {A,CD} \right)\\
 = \frac{{\left| {7.7 - 3.4 + 5} \right|}}{{\sqrt {{7^2} + {{\left( { - 3} \right)}^2}} }}.\frac{{\left| {3.7 - 7.4 - 1} \right|}}{{\sqrt {{3^2} + {7^2}} }} = \frac{{1008}}{{29}}
\end{array}\)

Câu 3:  Viết phương trình đường tròn có tâm nằm trên đường thẳng Δ: x + y – 3 =0 và đi qua hai điểm A(-1; 3), B(1; 4)

Hướng dẫn giải

Do tâm nằm trên đường thẳng ∆: x +y – 3 = 0 nên tâm I(x; 3 – x). Mà đường tròn đi qua A(-1; 3), B(1;4) nên IA2 = IB2 <=> (x+1)2+(-x)2=(x-1)2+(-1-x)2

\( \Leftrightarrow x = \frac{1}{2} \Rightarrow I\left( {\frac{1}{2};\frac{5}{2}} \right)\)

Bán kính \(R = IA = \sqrt {{{\left( {\frac{1}{2} + 1} \right)}^2} + {{\left( {\frac{5}{2} - 3} \right)}^2}}  = \frac{{\sqrt {10} }}{2}\)

Vậy phương trình đường tròn là 

\({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{5}{2}} \right)^2} = \frac{5}{2} \Leftrightarrow {x^2} + {y^2} - x - 5y + 4 = 0\)

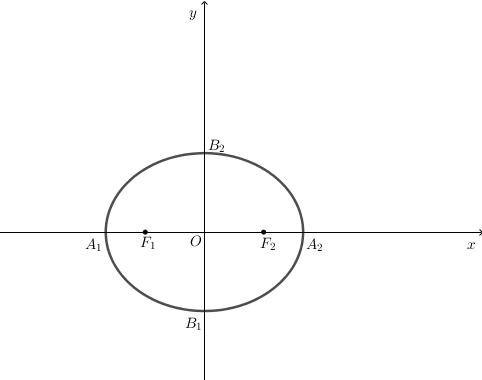
Câu 4: Cho elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{25}} = 1\)

Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.

Hướng dẫn giải

Ta có a2 = 25⇒ a = 5, b2 = 16 ⇒ b = 4

Vậy c2 = a2 - b2 = 25 - 16 = 9 ⇒ c = 3

Các đỉnh: \({A_1}\left( { - 5;0} \right),{A_2}\left( {5;0} \right),{B_1}\left( {0; - 4} \right),{B_2}\left( {0;4} \right)\)

Các tiêu điểm: \({F_1}\left( { - 3;0} \right),{F_2}\left( {3;0} \right)\)

Câu 1: Cho đường thẳng d: 2x−3y+3 = 0 và điểm A(1;0)

a) Với điều kiện nào của x và y thì điểm M(x, y) thuộc nửa mặt phẳng có bờ d và chứa gốc tọa độ O? Chứng minh điểm A nằm trong nửa mặt phẳng đó.

b) Tìm điểm đối xứng với điểm O qua đường thẳng d.

c) Tìm điểm M trên d sao cho chu vi tam giác OMA nhỏ nhất.

Câu 2: Cho đường tròn (C): x²+y² = 9 và điểm A(-1;4)

a) Viết phương trình của các tiếp tuyến của (C) kẻ từ A.

b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.

Câu 3: Cho \(\left( E \right):\frac{{{x^2}}}{25} + \frac{{{y^2}}}{9} = 1\) và hypebol \(\left( H \right):\frac{{{x^2}}}{25} - \frac{{{y^2}}}{9} = 1\).

a) Tìm tọa độ các tiêu điểm của (E) và (H).

b) Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.

c) Tìm tọa độ các giao điểm của (E) và (H).

Câu 4: Cho đường thẳng Δ: x−2y−2m = 0 và elip \(\left( E \right):\frac{{{x^2}}}{25} + \frac{{{y^2}}}{16} = 1\).

a) Với giá trị nào của m thì Δ cắt (E) tại hai điểm phân biệt?

b) Với giá trị nào của m thì Δ cắt (E) tại một điểm duy nhất?

Câu 1: Phương trình tổng quát của đường thẳng ∆ đi qua điểm M(1;3) và có vectơ pháp truyến \(\overrightarrow n  = \left( {5; - 2} \right)\) là:

A.  5(x+1) – 2(y+3) = 0

B. 5(x – 1) – 2(y – 3) = 0

C. (x – 5) + 3(y+2) = 0

D. (x+5) + 3(y – 2) = 0

Câu 2: Cho các điểm M(1; 1), N(3; -2), P(-1; 6). Phương trình các đường thẳng qua M cách đều N, P là

A. x – 2y + 1 = 0 và y = 1

B. 2x – y – 1 = 0 và x – y = 0

C. 2x + y – 3 = 0 và x = 1

D. 2x – 3y + 1 = 0 và 2x + y – 3 = 0

Câu 3: Cho đường tròn tiếp xúc với cả đường thẳng d₁: x+2y-4=0, d₂: x+2y+6=0. Khi đó diện tích hình tròn là

A. 5π

B. 10π

C. 20π

D. 40π

Câu 4: Cho đường tròn (C) có đường kính là AB với A(5; 1), B(1; -3). Khi đó phương trình của (C) là:

A. x²+y²+2x+2y+9=0

B.  x²+y²-6x+2y+2=0

C. x²+y²-2x-2y-7=0

D. x²+y²-6x+2y+15=0

Câu 5: Phương trình chính tắc của elip có độ dài trục nhỏ bằng 12, độ dài tiêu cự bằng 8 là

A. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\)

B. \(\frac{{{x^2}}}{{52}} + \frac{{{y^2}}}{{36}} = 1\)

C. \(\frac{{{x^2}}}{{208}} + \frac{{{y^2}}}{{144}} = 1\)

D. \(\frac{{{x^2}}}{{144}} + \frac{{{y^2}}}{{80}} = 1\)

Câu 6: Cho elip có phương trình: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\). Đường thẳng x = 1 cắt elip theo dây cung có độ dài là:

A. \(\frac{{\sqrt {105} }}{2}\)

B. \(\frac{{\sqrt {53} }}{2}\)

C. \(\frac{{\sqrt {87} }}{2}\)

D. \(\frac{{\sqrt {19} }}{2}\)

Qua bài học này, các em đạt được những mục tiêu sau:

• Nắm được kiến thức về Phương pháp tọa độ trong không gian.
• Ôn lại phương pháp giải toán liên quan.