Toán 10 Chương 5 Bài 4: Phương sai và độ lệch chuẩn

- Phương sai là trung bình cộng của các bình phương độ lệch của mỗi số liệu thống kê. 

- Công thức tính phương sai:

• Trường hợp bảng phân bố tần số, tần suất

\(\begin{array}{l}
{s^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{x_k} - \overline x } \right)}^2}} \right]\\
 = {f_1}{\left( {{x_1} - \overline x } \right)^2} + {f_2}{\left( {{x_2} - \overline x } \right)^2} + ... + {f_k}{\left( {{x_k} - \overline x } \right)^2}
\end{array}\)

Trong đó \(n_i;\,\,f_i\) lần lượt là tần số, tần suất cua giá trị x_i; n là số các số liệu thống kê (n=n₁+n₂+...+n_k); \({\overline x }\) là số trung bình cộng của các số liệu đã cho.

• Trường hợp bảng phân bố tần số, tần suất ghép lớp

\(\begin{array}{l}
{s^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\
 = {f_1}{\left( {{c_1} - \overline x } \right)^2} + {f_2}{\left( {{c_2} - \overline x } \right)^2} + ... + {f_k}{\left( {{c_k} - \overline x } \right)^2}
\end{array}\)

Trong đó \(c_i;\,\,n_i;\,\,f_i\) lần lượt là giá trị đại diện, tần số, tần suất của lớp thứ i; n là số các số liệu thống kê (n=n₁+n₂+...+n_k); \({\overline x }\) là số trung bình cộng của các số liệu đã cho.

- Phương pháp tính phương sai: 

• Tính trung bình cộng.
• Tính độ lệch của mỗi số liệu thống kê.
• Áp dụng công thức.

- Ngoài ra có thể dùng công thức:

\({s^2} = \overline {{x^2}}  - {\left( {\overline x } \right)^2}\)

trong đó \(\overline {{x^2}} \) là trung bình cộng của các bình phương số liệu thống kê và

\(\overline {{x^2}}  = \frac{1}{n}\sum\limits_{i = 1}^k {{n_i}{x^2}_i}  = \sum\limits_1^k {{f_i}{x^2}_i} \) (đối với bảng phân bố tần số, tần suất)

\(\overline {{x^2}}  = \frac{1}{n}\sum\limits_{i = 1}^k {{n_i}{c_i}^2}  = \sum\limits_1^k {{f_i}{c_i}^2} \) (đối với bảng phân bố tần số, tần suất ghép lớp)

- Căn bậc hai của phương sai được gọi là độ lệch chuẩn. Ký hiệu là s và \(s = \sqrt {{s^2}} \)

- Ý nghĩa: Phương sai s² và độ lệch chuẩn s đều được dùng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình cộng). Nhưng khi cần chú ý đến đơn vị đo thì ta dùng s vì s có đơn vị đo với dấu hiệu được nghiên cứu.

Câu 1:  Tính số trung bình cộng, phương sai, độ lệch chuẩn của bảng sau

Hướng dẫn giải

• Số trung bình cộng:

\(\displaystyle \overline x  = \frac{{16,7}}{{100}}.16 + \frac{{43,3}}{{100}}.18 \) \(+ \dfrac{{36,7}}{{100}}.20 + \dfrac{{3,3}}{{100}}.22 = 18,5\)

• Phương sai:

\(\displaystyle {s^2} = {{16,7} \over {100}}{(16 - 18,5)^2}\) \(\displaystyle + {{43,3} \over {100}}{(18 - 18,5)^2}  + {{36,7} \over {100}}{(20 - 18,5)^2} \) \(\displaystyle + {{3,3} \over {100}}{(22 - 18,5)^2} \approx 2,382\)

• Độ lệch chuẩn:

\(s = \sqrt {{s^2}}  = \sqrt {2,382}  \approx 1,54\)

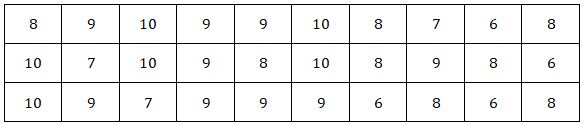
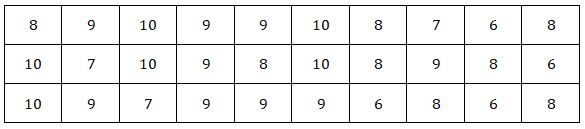
Câu 2: Hai xạ thủ cùng tập bắn, mỗi người đã bắn 30 viên đạn vào bia. Kết quả được ghi lại ở các bảng sau.

Điểm số của xạ thủ A

Điểm số của xạ thủ B

a) Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê cho ở hai bảng trên.

b) Xét xem trong lần tập bắn này, xạ thủ nào bắn chụm hơn?

Hướng dẫn giải

a) Điểm số của xạ thủ A có: \(\overline x  \approx 8,3\)điểm, \(s_1^2 \approx 1,6;{s_1} \approx 1,27\)điểm.

Điểm số của xạ thủ B có \(\overline y  \approx 8,4\)điểm, \(s_2^2 \approx 1,77;{s_1} \approx 1,33\)điểm.

b) \(\overline x  \approx \overline y  = 8,4\)điểm, \(s_1^2 > s_1^2\), như vậy mức độ phân tán của các điểm số (so với số trung bình) của xạ thủ A là bé hơn.

Vì vậy, trong lần tập bắn này, xạ thủ A bắn chụm hơn.

Câu 1: Hai lớp 10C, 10D của một trường Trung học phổ thông đồng thời làm bài thi môn Ngữ văn theo cùng một đề thi. Kết quả thi được thình bày ở hai bảng phân bố tần số sau đây:

Điểm thi ngữ văn của lớp 10C

Điểm thi ngữ văn của lớp 10D

a) Tính các số trung bình cộng, phương sai, độ lệch chuẩn của các bảng phân bố tần số đã cho.

b) Xét xem kết quả làm bài thi của môn Ngữ văn ở lớp nào là đồng đều hơn?

Câu 2: Cho hai bảng phân bố tần số ghép lớp

Khối lượng của nhóm cá mè thứ 1

Khối lượng của nhóm cá mè thứ 2

a) Tính các số trung bình cộng của các bảng phân bố tần số ghép lớp đã cho.

b) Tính phương sai của các bảng phân bố tần số ghép lớp đã cho.

c) Xét xem nhóm cá nào có khối lượng đồng đều hơn?

Câu 1: Nếu đơn vị của số liệu là kg thì đơn vị của phương sai là?

A. kg

B. kg^₂

C. Không có đơn vị 

D. kg/2

Câu 2: Tỉ số giữa tần số và kích thước mẫu được gọi là

A. Mốt 

B. Phương sai 

C. Tần suất 

D. Số trung vị

Câu 3: Chọn câu đúng trong bốn phương án trả lời đúng sau đây:

Độ lệch chuẩn là?

A. Bình phương của phương sai 

B. Một nửa của phương sai

C. Căn bậc hai của phương sai 

D. Không phải là các công thức trên.

Câu 4: Cho dãy số liệu thống kê: 1, 2, 3, 4, 5, 6, 7, 8. Độ lệch chuẩn của dãy số liệu thống kê gần bằng

A. 2,30

B. 3,30

C. 4,30

D. 5,30

Qua bài học này, các em cần nắm được những nội dung sau:

• Các cách tính Phương sai và độ lệch chuẩn.
• So sánh mức độ phân tán của các số liệu thống kê dựa vào số trung bình cộng.