Toán 10 Chương 2 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
Mời các em cùng tham khảo nội dung bài giảng Các hệ thức lượng trong tam giác và giải tam giác do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1.Tóm tắt lý thuyết
1.1. Định lí côsin trong tam giác
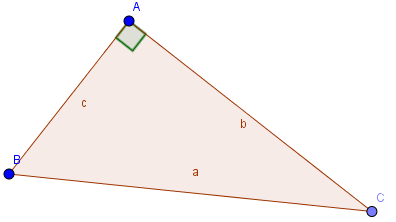
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
\(\eqalign{
& {a^2} = {b^2} + {c^2} - 2bc.{\mathop{\rm cosA}\nolimits} (1) \cr
& {b^2} = {a^2} + {c^2} - 2ac{\mathop{\rm cosB}\nolimits} (1) \cr
& {c^2} = {a^2} + {b^2} - 2ab\cos C(3) \cr} \)
\(\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc}\)
\(\cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}\)
\(\cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}\)
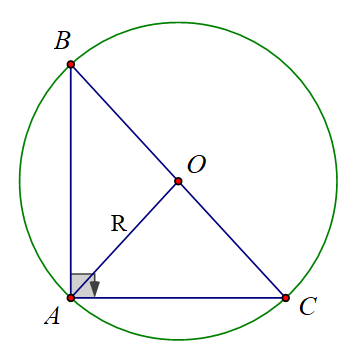
1.2. Định lí sin trong tam giác
Định lí: Trong tam giác \(ABC\) bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là
\(\frac{a}{sin A}= \frac{b}{sin B} = \frac{c}{sin C} = 2R\)
với \(R\) là bán kính đường tròn ngoại tiếp tam giác
1.3. Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
Cho tam giác ABC có đường trung tuyến AM.
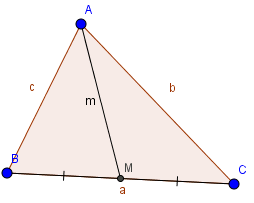
Gọi \(m_a;m_b;m_c\) lần lượt là các đường trung tuyến ứng với các cạnh a, b, c. Khi đó:
\(m_{a}^{2}=\frac{b^2+c^2}{2}-\frac{a^2}{4}\)
\(m_{b}^{2}=\frac{a^2+c^2}{2}-\frac{b^2}{4}\)
\(m_{c}^{2}=\frac{a^2+b^2}{2}-\frac{c^2}{4}\)
1.4. Diện tích tam giác
Ta kí hiệu ha, hb và hc là các đường cao của tam giác \(ABC\) lần lượt vẽ từ các đình \(A, B, C\) và \(S\) là diện tích tam giác đó.
Diện tích \(S\) của tam giác \(ABC\) được tính theo một trong các công thức sau
\(S=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c\)
\(S=\frac{1}{2}ab.sinC=\frac{1}{2}ac.sinB=\frac{1}{2}bc.sinA\)
\(S=\frac{abc}{4R}\)
\(S=pr\)
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
1.5. Giải tam giác và ứng dụng thực tế
Giải tam giác là tính độ dài các cạnh và số đo các góc của tam giác dựa trên điều kiện cho trước.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại
b) Giải tam giác khi biết hai cạnh và góc xen giữa
Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng định lí cosin để tính góc
\(\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc}\)
\(\cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}\)
\(cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}\)
Chú ý:
- Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
- Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
2. Bài tập minh họa
Câu 1: Cho tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến ma của tam giác ABC đã cho.
Hướng dẫn giải
\(\eqalign{
& m_a^2 = {{2({b^2} + {c^2}) - {a^2}} \over 4} = {{2({8^2} + {6^2}) - {7^2}} \over 4} = {{151} \over 4} \cr
& \Rightarrow {m_a} = {{\sqrt {151} } \over 2} \cr} \)
Câu 2: Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.
Chứng minh hệ thức: \({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = 2R\)
Hướng dẫn giải
Do tam giác ABC vuông tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC ⇒ BC = a = 2R
Ta có:
\(\eqalign{
& \sin A = \sin {90^0} = 1 = {a \over a} = {a \over {2R}} \cr
& \Rightarrow {a \over {\sin A}} = 2R \cr
& \sin B = {b \over a} = {b \over {2R}} \Rightarrow {b \over {\sin B}} = 2R \cr
& \sin C = {c \over a} = {c \over {2R}} \Rightarrow {c \over {\sin C}} = 2R \cr} \)
Câu 3: Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
Hướng dẫn giải
Theo định lí sin ta có:
\({a \over {\sin A}} = 2R \Rightarrow R = {a \over {2\sin A}}\)
Tam giác ABC đều nên A = 600
\(\eqalign{
& \Rightarrow \sin A = {{\sqrt 3 } \over 2} \cr
& \Rightarrow R = {a \over {2\sin A}} = {a \over {2.{{\sqrt 3 } \over 2}}} = {a \over {\sqrt 3 }} \cr} \)
Câu 4: Dựa vào công thức (1) và định lý sin. Hãy chứng minh: \(S = {{abc} \over {4R}}\)
Hướng dẫn giải
Theo định lý Sin, ta có:
\({c \over {\sin C}} = 2R \Rightarrow \sin C = {c \over {2R}}\)
Khi đó:
\(S = {1 \over 2}ab.\sin C = {1 \over 2}ab.{c \over {2R}} = {{abc} \over {4R}}\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác ABC vuông tại A có \(\widehat B = {37^o}\) và cạnh a=48cm. Tính \(\widehat C\), cạnh b, cạnh c và đường cao ha
Câu 2: Cho tam giác ABC biết các cạnh a = 25cm; b = 36cm và c = 53cm. Tính các góc \(\widehat A,\,\,\widehat B,\,\,\widehat C\)
Câu 3: Tính diện tích S của tam giác có số đo các cạnh lần lượt là 3, 4 và 5.
3.2. Bài tập trắc nghiệm
Câu 1: Diện tích tam giác ABC có độ dài các cạnh là 6, 8, 10 là:
A. \(20\)
B. \(24\)
C. \(36\)
D. \(48\)
Câu 2: Cho tam giác ABC có các cạnh a, b, c lần lượt là 10, 15, 18. Độ dài đường trung tuyến \(b_m\) bằng:
A. \(\approx 11,39\)
B. \(\approx 12,48\)
C. \(\approx 13,23\)
D. \(\approx 15,61\)
Câu 3: Cho đường tròn (O;3) nội tiếp tam giác ABC vuông tại A. Biết rằng tam giác BDE đều (như hình vẽ). Diện tích tam giác ABC là:
A. \(9+9\sqrt{3}\)
B. \(18+9\sqrt{3}\)
C.\(18+18\sqrt{3}\)
D. \(27+18\sqrt{3}\)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung cơ bản sau:
- Nhớ công thức Định lý cosin, Định lý sin.
- Áp dụng vào giải tam giác.
.JPG)
