Toán 10 Chương 2 Bài 1: Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
Mời các em cùng tham khảo nội dung bài giảng Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Tóm tắt ký thuyết
1.1. Định nghĩa
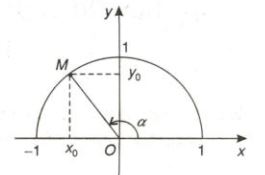
Với mỗi góc \(\alpha(0^o\leq \alpha\leq 180^o)\), ta xác định điểm M trên nửa đường tròn sao cho \(\widehat{MOx}=\alpha\). Giả sử điểm \(M(x_0;y_0)\). Khi đó:
Tung độ \(y_0\) của điểm M được gọi là sin của góc \(\alpha\), ta kí hiệu là \(\sin\alpha\)
Hoành độ \(x_0\) của điểm M được gọi là cosin của góc \(\alpha\), ta kí hiệu là \(\cos\alpha\).
Tỉ số \(\frac{y_0}{x_0}\) \((x_0\neq 0)\) được gọi là tan của góc \(\alpha\), ta kí hiệu là \(\tan\alpha\)
Tỉ số \(\frac{x_0}{y_0}\) \((y\neq 0)\) được gọi là côtan của góc \(\alpha\), ta kí hiệu là \(\cot\alpha\)
Tính chất:
Nếu hai góc bù nhau thì sin của chúng bằng nhau, còn cos, tan và cot của chúng đối nhau, cụ thể là:
-
\(\sin(180^o-\alpha)=\sin\alpha\)
-
\(\cos(180^o-\alpha)=-\cos\alpha\)
-
\(\tan(180^o-\alpha)=-\tan\alpha(\alpha\neq 90^o)\)
-
\(\cot(180^o-\alpha)=-\cot\alpha(0^o<\alpha<180^o)\)
1.2. Giá trị lượng giác của các góc đặc biệt
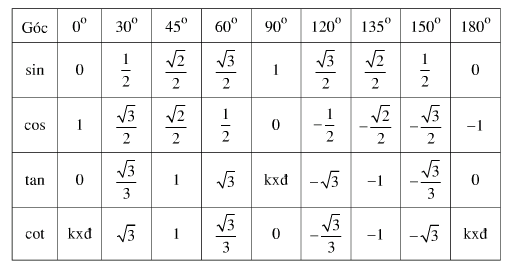
2. Bài tập minh họa
Tìm các giá trị lượng giác của các góc 1200, 1500.
Hướng dẫn giải
Các giá trị lượng giác của góc 120o (ứng với \(\alpha = {150^0}\)) là:
\(\begin{array}{l}
\sin {120^0} = \sin \left( {{{180}^0} - {{120}^0}} \right)\\
= \sin {60^0} = \frac{{\sqrt 3 }}{2}\\
\cos {120^0} = - \cos \left( {{{180}^0} - {{120}^0}} \right)\\
= - \cos {60^0} = - \frac{1}{2}\\
\tan {120^0} = - \tan \left( {{{180}^0} - {{120}^0}} \right)\\
= - \tan {60^0} = - \sqrt 3 \\
\cot {120^0} = - \cot \left( {{{180}^0} - {{120}^0}} \right)\\
= - \cot {60^0} = - \frac{1}{{\sqrt 3 }}
\end{array}\)
Câu 2: Khi nào góc giữa hai vectơ bằng 0o ? Khi nào góc giữa hai vectơ bằng 180o.
Hướng dẫn giải
Góc giữa hai vectơ bằng 0o khi chúng cùng hướng với nhau.
Góc giữa hai vectơ bằng 180o khi chúng ngược hướng với nhau.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho \(\Delta ABC\), chứng minh rằng
a) \(\sin C=\sin (A+B)\).
b) \(\cos C=-\cos (A+B)\).
Câu 2: Cho góc x, với \(\cos x = \frac{3}{5}\) tính \(A = 2{\cos ^2}x + 3{\sin ^2}x\).
Câu 3: Cho hình vuông ABCD. Tính \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {CB} } \right);\,\,\sin \left( {\overrightarrow {BD} ,\overrightarrow {CA} } \right)\)
3.2. Bài tập trắc nghiệm
Câu 1: Giá trị của biểu thức: \(\sin ^2x+\cos ^2x\) là:
A. 0
B. 1
C. \(2\cos ^2x\)
D. \(2\sin ^2x\)
Câu 2: Giá trị của biểu thức \(sin75^o+sin105^o\) là:
A. 0
B. \(2\sin ^275^o\)
C. \(\sin ^275^o\)
D. \(2\sin 75^o\)
Câu 3: Giá trị của biểu thức \(\sin^290^o+\cos^20^o+\tan60^o-\cot45^o\) là:
A. \(\sqrt{3}+1\)
B. \(\sqrt{3}-1\)
C. \(\sqrt{3}+2\)
D. \(\sqrt{3}-2\)
Câu 4: Giá trị của biểu thức: \(\sin45^o+\cos77^o-3\sin33^o+51\cos^288^o+\cot0^o\) là
A. \(\sin 45^o\)
B. \(2\cos 77^o\)
C. \(102\cos 88^o\)
D. không xác định
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Định nghĩa và tính chất quan trọng của giá trị lượng giác.
- Giá trị lượng giác của các góc đặc biệt.