Toán 10 Chương 4 Bài 4: Bất phương trình bậc nhất hai ẩn

Định nghĩa: Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by \le c\) \((ax + by < c;ax + by \ge c;ax + by > c)\) trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.

Ví dụ: Bất phương trình 7x + 3y < -3; 2x +4y > 4;...

Cặp số \((x_0;y_0)\) sao cho \(ax_0+ by_0\le c\) là một bất đẳng thức đúng được gọi là một nghiệm của bất phương trình \(ax + by \le c\).

- Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

- Khái niệm miền nghiệm: Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm bất phương trình \(ax + by \le c{\rm{ }}\) được gọi là miền nghiệm của nó.

- Biểu diễn miền nghiệm: Quy tắc thực hành biểu diễn hình học miền nghiệm ( hay biểu diễn miền nghiệm) của bất phương trình \(ax + by \le c{\rm{ }}\) ( tương tự cho bất phương  \(ax + by \ge c\))

Bước 1: Trên mặt phẳng xy, vẽ đường thẳng \(\Delta :ax + by = c\)

Bước 2: Lấy một điểm \({M_0}\left( {{x_0};{y_0}} \right)\) không thuộc \(\Delta \) ( ta thường lấy gốc tọa độ O)

Bước 3: Tính \(ax_0 + by_0\) và so sánh \(ax_0 + by_0\) với c

Bước 4: Kết luận

• Nếu \(ax_0 + by_0 < c\) thì nửa mặt phẳng bờ \(\Delta \) chứa \({M_0}\) là miền nghiệm của \(ax + by \le c{\rm{ }}\)
• Nếu \(ax_0 + by_0 > c\) thì nửa mặt phẳng bờ \(\Delta \) không chứa \({M_0}\) là miền nghiệm của \(ax + by \le c{\rm{ }}\)

Chú ý: Miền nghiệm của bất phương trình \(ax + by \le c{\rm{ }}\) bỏ đi đường thẳng là miền nghiệm của bất phương trình \(ax + by < c\)

- Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x, y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

- Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính. 

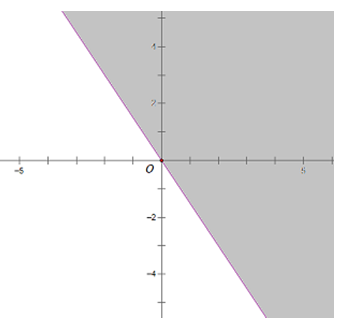
Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn: -3x + 2y > 0.

Hướng dẫn giải

- Vẽ đường thẳng (d): -3x + 2y = 0

- Cho x=0 thì y=0 nên ta được điểm (0;0) thuộc đồ thị hàm số.

- Cho x=2 thì \( - 3.2 + 2y = 0 \Leftrightarrow  - 6 + 2y = 0\) \( \Leftrightarrow 2y = 6 \Leftrightarrow y = 3\) nên ta được điểm (2;3) thuộc đồ thị hàm số.

Vẽ (d):

Lấy điểm A(1; 1), ta thấy A ∉(d) và có: -3.1 + 2.1 < 0 nên nửa mặt phẳng bờ (d) không chưá A là miền nghiệm của bất phương trình. (miền hình không bị tô đậm)

Câu 2: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn

\(\left\{ \matrix{
2x - y \le 3 \hfill \cr
2x + 5y \le 12x + 8 \hfill \cr} \right.\)

Hướng dẫn giải

\(\left\{ \matrix{
2x - y \le 3 \hfill \cr
2x + 5y \le 12x + 8 \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
2x - y \le 3 \hfill \cr
10x -5y \ge -8 \hfill \cr} \right.\)

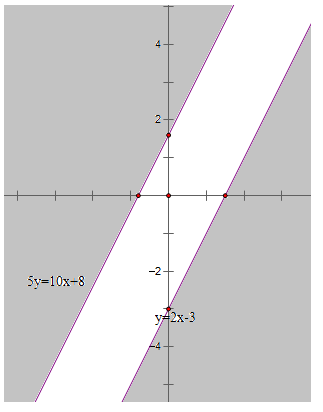
Vẽ hai đường thẳng \(2x - y = 3 \Leftrightarrow y = 2x - 3\) và \(10x - 5y =  - 8 \Leftrightarrow 5y = 10x + 8\) ta được:

Lấy điểm O(0;0), ta thấy O không thuộc cả 2 đường thẳng trên và \(2.0-0 ≤ 3\) và \(10.0-5.0\ge -8\) nên phần được giới hạn bởi 2 đường thẳng trên chứa điểm O( phần ko tô đậm) là nghiệm của hệ bất phương trình.

Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn \(- x + 3y > 4\)

Câu 2: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn 

\(\left\{ \begin{array}{l}
3x - 2y \le 3\\
x + 4y \le 3x + 5 \end{array} \right.\)

Câu 1: Xác định m để phương trình \(\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\) có ba nghiệm phân biệt lớn hơn –1.

A. \(m < - \frac{7}{2}\)

B. \(\left\{ \begin{array}{l} - 2 < m < 1\\ m \ne - \frac{{16}}{9} \end{array} \right.\)

C. \(\left\{ \begin{array}{l} - \frac{7}{2} < m < - 1\\ m \ne - \frac{{16}}{9} \end{array} \right.\)

D. \(\left\{ \begin{array}{l} - \frac{7}{2} < m < - 3\\ m \ne - \frac{{19}}{6} \end{array} \right.\)

Câu 2: Phương trình \(\left( {m + 1} \right){x^2} - 2\left( {m - 1} \right)x + {m^2} + 4m - 5 = 0\) có đúng hai nghiệm x₁, x₂ thoả 2 < x₁ < x₂. Hãy chọn kết quả đúng trong các kết quả sau

A. \( - 2 < m < - 1\)

B. \(m > 1\)

C. \( - 5 < m < - 3\)

D. \( - 2 < m < 1\)

Câu 3: Nghiệm dương nhỏ nhất của bất phương trình \(\left| {\left| {{x^2} - 4x - 5} \right| + 2x + 9} \right| \le \left| {{x^2} - x + 5} \right|\) gần nhất với số nào sau đây

A. 2,8

B. 3

C. 3,5

D. 4,5

Câu 4: Tìm m để \(\left| {4x - 2m - \frac{1}{2}} \right| > - {x^2} + 2x + \frac{1}{2} - m\) với mọi x?

A. m > 3

B. m < 1,5

C. m > 1,5

D. -2 < m < 3

Câu 5: Cho bất phương trình:\(\left| {{x^2} + x + a} \right| + \left| {{x^2} - x + a} \right| \le 2x\)( 1). Khi đó khẳng định nào sau đây đúng nhất?

A. (1) có nghiệm khi \(a \le \frac{1}{4}\)

B. Mọi nghiệm của (1) đều không âm

C. ( 1) có nghiệm lớn hơn 1 khi a < 0.

D. Tất cả đều đúng

Qua bài học này, các em cần nắm được các nội dung sau:

• Khái niệm cơ bản về bất phương trình bậc nhất hai ẩn
• Phương pháp biểu diễn tập nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn.