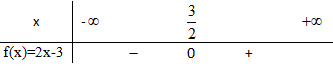Toán 10 Chương 4 Bài 3: Dấu của nhị thức bậc nhất

1.1.1. Nhị thức bậc nhất 

Nhị thức bậc nhất đối với x là biểu thức dạng ax + b, trong đó a và b là hai số cho trước, với a ≠ 0 và a được gọi là hệ số của x hay hệ số của nhị thức.

Ví dụ 1: \(f(x) = 5x - 1;{\rm{ }}g(x) = 4 +7x\)

1.1.2. Dấu của nhị thức bậc nhất

Định lý: Nhị thức bậc nhất f(x) = ax + b cùng dấu với hệ số a khi x lấy các giá trị trong khoảng \(\left( { - \frac{b}{a}; + \infty } \right)\) và trái dấu với hệ số a khi x lấy các giá trị trong khoảng \(\left( { - \infty ; - \frac{b}{a}} \right)\)

Kết quả của định lí trên được tóm tắt trong bảng sau:

Ta gọi bảng này là bảng xét dấu nhị thức f(x) = ax + b.

Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lý vè dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử. Lập bằng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương cũng được xét tương tự.

Ví dụ 2: Xét dấu biểu thức \(f(x) = \frac{{\left( {4x - 1} \right)\left( {x + 2} \right)}}{{ - 3x + 5}}\)

Hướng dẫn giải:

Giải các phương trình 

\(\begin{array}{l}
4x - 1 = 0 \Leftrightarrow x = \frac{1}{4}\\
x + 2 = 0 \Leftrightarrow x =  - 2\\
 - 3x + 5 = 0 \Leftrightarrow x = \frac{5}{3}
\end{array}\)

f(x) không xác định khi \(x = \frac{5}{3}\)

Lập bảng xét dấu chung 

Vậy f(x) > 0 khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( {\frac{1}{4};\frac{5}{3}} \right)\)

f(x) < 0 khi \(x \in \left( { - 2;\frac{1}{4}} \right) \cup \left( {\frac{5}{3}; + \infty } \right)\)

f(x) = 0 khi x = -2 hoặc \(x = \frac{1}{4}\)

Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức f(x).

1.3.1. Bất phương trình tích, bất phương trình chứa ẩn ở mẫu 

Phương pháp chung:

- Đặt điều kiện và quy đồng mẫu thức các phân phức.

- Xét dấu các nhị thức bậc nhất và kết luận nghiệm.

Ví dụ 3: Giải bất phương trình \(\frac{1}{{1 - x}} \ge 1\)

Hướng dẫn giải:

Ta biến đổi tương đương bất phương trình đã cho 

\(\frac{1}{{1 - x}} \ge 1 \Leftrightarrow \frac{1}{{1 - x}} - 1 \ge 0 \Leftrightarrow \frac{x}{{1 - x}} \ge 0\)

Xét dấu biểu thức \(f(x) = \frac{x}{{1 - x}}\) ta suy ra nghiệm của bất phương trình đã cho:

Vậy tập nghiệm của bất phương trình là \(S = \left[ {0;1} \right)\)

1.3.2. Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối 

Bằng cách áp dụng tính chất của giá trị tuyệt đối ta có thể dễ dàng giải các bất phương trình dạng \(\left| {f\left( x \right)} \right| \le a\) và \(\left| {f\left( x \right)} \right| \ge a\) với \(a > 0\) đã cho.

Với \(a>0\) ta có:

\(\left| {f\left( x \right)} \right| \le a \Leftrightarrow  - \,a \le f\left( x \right) \le a\)

\(\left| {f\left( x \right)} \right| \ge a \Leftrightarrow f\left( x \right) \le  - \,a\) hoặc \(f\left( x \right) \ge a\)

Ví dụ 4: Giải bất phương trình |-2x+1|+x-3 < 5

Hướng dẫn giải:

Theo định nghĩa giá trị tuyệt đối ta có: 

\(\left| { - 2x + 1} \right| = \left\{ {\begin{array}{*{20}{l}}
{ - 2x + 1,x \ge \frac{1}{2}}\\
{ - \left( { - 2x + 1} \right),x < \frac{1}{2}}
\end{array}} \right.\)

Giải các hệ bất phương trình:

\(\begin{array}{l}
\left\{ \begin{array}{l}
x \le \frac{1}{2}\\
\left( { - 2x + 1} \right) + x - 3 < 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \le \frac{1}{2}\\
x >  - 7
\end{array} \right. \Leftrightarrow  - 7 < x \le \frac{1}{2}\\
\left\{ \begin{array}{l}
x > \frac{1}{2}\\
\left( {2x - 1} \right) + x - 3 < 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x > \frac{1}{2}\\
x < 3
\end{array} \right. \Leftrightarrow \frac{1}{2} < x < 3
\end{array}\)

Nghiệm của bất phương trình đã cho là hợp của hai khoảng:

\(\left( { - 7;\frac{1}{2}} \right] \cup \left( {\frac{1}{2};3} \right) = \left( { - 7;3} \right)\)

Kết luận: Bằng cách áp dụng tính chất của giá trị tuyệt đối ta có thể dễ dàng giải các bất phương trình dạng \(\left| {f(x)} \right| \le a\) và \(f(x) \ge a\) với a > 0 đã cho.

Ta có:

\(\left| {f(x)} \right| \le a \Leftrightarrow  - a \le f(x) \le a\)

\(f(x) \ge a \Leftrightarrow f(x) \le a \vee f(x) \ge a\)

Câu 1: Xét dấu các nhị thức  \(f(x) = 2x - 5; \,\,\, g(x)=3-4x\)

Hướng dẫn giải:

Xét \(f(x) = 2x - 5\)

Hệ số a = 2 > 0 và có nghiệm là \({x_0} = \frac{5}{2}\)

Vậy f(x) > 0 khi \({x} > \frac{3}{2}\); f(x) < 0 khi \({x} < \frac{3}{2}\)

\(g(x) = 3-4x\) 

Hệ số a = -4 < 0 và có nghiệm \({x_0} = \frac{3}{4}\)

Vậy g(x) > 0 khi \({x} < \frac{3}{4}\); g(x) < 0 khi \({x} > \frac{3}{4}\)

Câu 2: Giải bất phương trình \(\frac{4}{{x - 1}} > \frac{7}{{2x + 1}}\)

Hướng dẫn giải:

\(\begin{array}{l}
\frac{4}{{x - 1}} > \frac{7}{{2x + 1}} \Leftrightarrow \frac{4}{{x - 1}} - \frac{7}{{2x + 1}} > 0\\
 \Leftrightarrow \frac{{4\left( {2x + 1} \right) - 7\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {2x + 1} \right)}} > 0 \Leftrightarrow \frac{{x + 11}}{{\left( {x - 1} \right)\left( {2x + 1} \right)}} > 0
\end{array}\) (*)

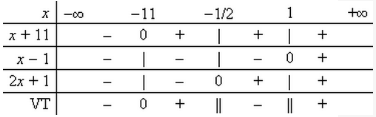
Bảng xét dấu 

Từ bảng xét dấu trên ta suy ra tập nghiệm của bất phương trình (*) là:

\(S = \left( { - 11; - \frac{1}{2}} \right) \cup \left( {1; + \infty } \right)\)

Câu 1: Xét dấu các nhị thức  \(f(x) = 3x - 4;{\rm{ }}g(x) = 2 - 4x\)

Câu 2: Xét dấu biểu thức \(f(x) = \left( {3x - 2} \right)\left( { -2x + 5} \right)\)

Câu 3: Giải bất phương trình x³ - 3x < 0

Câu 4: Giải bất phương trình \(\frac{3}{{x - 2}} > \frac{3}{{3x + 2}}\)

Câu 5: Giải bất phương trình \(\left| {2x + 1} \right| \le x - 1\)

Câu 1: Bất phương trình \(\sqrt { - {x^2} + 6x - 5} > 8 - 2x\) có nghiệm là: 

A. \(3 < x \le 5\)

B. \(2 < x \le 3\)

C. \( - 5 < x \le - 3\)

D. \( - 3 < x \le - 2\)

Câu 2: Bất phương trình: \(\sqrt {2x + 1} < 3 - x\) có nghiệm là:

A. \(\left[ { - \frac{1}{2};4 - 2\sqrt 2 } \right)\)

B. \(\left( {3;4 + 2\sqrt 2 } \right)\)

C. \(\left( {4 - 2\sqrt 2 ;3} \right)\)

D. \(\left( {4 + 2\sqrt 2 ; + \infty } \right)\)

Câu 3: Nghiệm của hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}} {2{x^2} - x - 6 \le 0}\\ {{x^3} + {x^2} - x - 1 \ge 0} \end{array}} \right.\) là:

A. \(-2 \le x \le 3\)

B. \(-1 \le x \le 3\)

C. \(\left[ \begin{array}{l} 1 \le x \le 2\\ x = -1 \end{array} \right.\)

D. \(1 \le x \le 2\)

Câu 4: Bất phương trình: \(\left| {{x^4} - 2{x^2} - 3} \right| \le {x^2} - 5\) có bao nhiêu nghiệm nghiệm nguyên?

A. 0

B. 1

C. 2

D. Nhiều hơn 2 nhưng hữu hạn.

Câu 5: Cho bất phương trình: \({x^2} - 2x \le \left| {x - 2} \right| + ax - 6\). Giá trị dương nhỏ nhất của a để bất phương trình có nghiệm gần nhất với số nào sau đây:

A. 0,5

B. 1,6

C. 2,2

D. 2,6

Qua bài học này, các em cần nắm được các nội dung sau:

• Khái niệm cơ bản về Dấu của nhị thức bậc nhất 

• Phương pháp để giải bất phương trình tích

• Phương pháp giải bất phương trình chứa ẩn ở mẫu thức

• Phương pháp giải bất phương trình chứa ẩn trong dấu giá trị tuyệt đối