Giải bài tập SGK Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Giải các hệ phương trình sau bằng phương pháp cộng đại số.

a) \(\left\{\begin{matrix} 3x + y =3 & & \\ 2x - y = 7 & & \end{matrix}\right.\)

b) \(\left\{\begin{matrix} 2x + 5y =8 & & \\ 2x - 3y = 0& & \end{matrix}\right.\)

c) \(\left\{\begin{matrix} 4x + 3y =6 & & \\ 2x + y = 4& & \end{matrix}\right.\)

d) \(\left\{\begin{matrix} 2x + 3y =-2 & & \\ 3x -2y = -3& & \end{matrix}\right.\)

e) \(\left\{\begin{matrix} 0,3x + 0,5y =3 & & \\ 1,5x -2y = 1,5& & \end{matrix}\right.\)

Phương pháp giải

• Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau.
• Áp dụng quy tắc cộng đại số để được hệ phương trình mới trong đó có một phương trình một ẩn.
• Giải phương trình một ẩn, tìm được nghiệm thay vào phương trình còn lại ta được nghiệm của hệ đã cho. 

Hướng dẫn giải

Câu a

 \(\Leftrightarrow \left\{\begin{matrix} 3x + y =3 & & \\ 5x = 10 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y =-3 & & \\ x = 2 & & \end{matrix}\right.\)

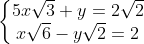
Vậy nghiệm của hệ phương trình là \((x;y)=(2;-3)\)

Câu b

\(\Leftrightarrow \left\{\begin{matrix} 2x + 5y =8 & & \\ 8y = 8& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} x =\frac{3}{2} & & \\ y = 1& & \end{matrix}\right.\)

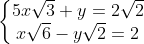
Vậy nghiệm của hệ phương trình là \((x;y)=\left ( \frac{3}{2};1 \right )\)

Câu c

 \(\Leftrightarrow \left\{\begin{matrix} 4x + 3y =6 & & \\ 6x + 3y = 12& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 4x + 3y =6 & & \\ 2x = 6& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y =-2 & & \\ x = 3& & \end{matrix}\right.\)

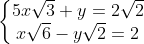
Vậy nghiệm của hệ phương trình là \((x;y)=(3;-2)\)

Câu d

\(\Leftrightarrow \left\{\begin{matrix} 6x + 9y =-6 & & \\ 6x -4y = -6& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 6x + 9y =-6 & & \\ 13y = 0& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} x=-1 & & \\ y = 0& & \end{matrix}\right.\)

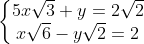
Vậy nghiệm của hệ phương trình là \((x;y)=(-1;0)\)

Câu e

\(\Leftrightarrow \left\{\begin{matrix} 1,2x + 2y =12 & & \\ 1,5x -2y = 1,5& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 1,2x + 2y =12 & & \\ 2,7x = 13,5& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y =3 & & \\ x = 5& & \end{matrix}\right.\)

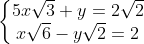
Vậy nghiệm của hệ phương trình là \((x;y)=(5;3)\)

Giải các hệ phương trình sau bằng phương pháp cộng đại số

a) \(\left\{\begin{matrix} x\sqrt{2} - 3y = 1 & & \\ 2x + y\sqrt{2}=-2 & & \end{matrix}\right.\)

b) \(\left\{\begin{matrix} 5x\sqrt{3}+ y = 2\sqrt{2}& & \\ x\sqrt{6} - y \sqrt{2} = 2& & \end{matrix}\right.\)

Phương pháp giải

• Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau.
• Áp dụng quy tắc cộng đại số để được hệ phương trình mới trong đó có một phương trình một ẩn.
• Giải phương trình một ẩn, tìm được nghiệm thay vào phương trình còn lại ta được nghiệm của hệ đã cho. 

Hướng dẫn giải

Câu a

\(\Leftrightarrow \left\{\begin{matrix} 2x - 3y\sqrt{2} = \sqrt{2} & & \\ 2x + y\sqrt{2}=-2 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 2x - 3y\sqrt{2} = \sqrt{2} & & \\4y\sqrt{2}=-2-\sqrt{2} & & \end{matrix}\right.\)

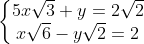
\(\Leftrightarrow \left\{\begin{matrix} x = \frac{-6+\sqrt{2}}{8} & & \\y=-\frac{1+\sqrt{2}}{4} & & \end{matrix}\right.\)

Vậy nghiệm của hệ phương trình là \((x;y)=\left ( \frac{-6+\sqrt{2}}{8};-\frac{1+\sqrt{2}}{4} \right )\)

Câu b

\(\Leftrightarrow \left\{\begin{matrix} 5x\sqrt{6}+ y\sqrt{2} = 4& & \\ x\sqrt{6} - y \sqrt{2} = 2& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 6x\sqrt{6}=6& & \\ x\sqrt{6} - y \sqrt{2} = 2& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} x=\frac{\sqrt{6}}{6}& & \\ y=-\frac{\sqrt{2}}{2}& & \end{matrix}\right.\)

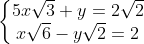
Vậy nghiệm của hệ phương trình là \((x;y)=\left ( \frac{\sqrt{6}}{6};-\frac{\sqrt{2}}{2} \right )\)

Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) \(\left\{\begin{matrix} -5x + 2y = 4 & & \\ 6x - 3y =-7 & & \end{matrix}\right.\)

b) \(\left\{\begin{matrix} 2x - 3y = 11& & \\ -4x + 6y = 5 & & \end{matrix}\right.\)

c) \(\left\{\begin{matrix} 3x - 2y = 10& & \\ x - \dfrac{2}{3}y = 3\dfrac{1}{3} & & \end{matrix}\right.\)

Phương pháp giải

• Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau.
• Áp dụng quy tắc cộng đại số để được hệ phương trình mới trong đó có một phương trình một ẩn.
• Giải phương trình một ẩn, tìm được nghiệm thay vào phương trình còn lại ta được nghiệm của hệ đã cho. 

Hướng dẫn giải

Câu a

 \(\Leftrightarrow \left\{\begin{matrix} 15x -6y = -12 & & \\ 12x - 6y =-14 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} -5x +2y = 4 & & \\ 3x=2 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y = \frac{11}{3} & & \\ x=\frac{2}{3} & & \end{matrix}\right.\)

Vậy nghiệm của hệ phương trình là \((x;y)=\left ( \frac{2}{3};\frac{11}{3} \right )\)

Câu b

 \(\Leftrightarrow \left\{\begin{matrix} -4x +6y = -22& & \\ -4x + 6y = 5 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 0x+0y=27& & \\ -4x + 6y = 5 & & \end{matrix}\right.\) (Vậy hệ phương trình vô nghiệm)

Câu c

 \(\Leftrightarrow \left\{\begin{matrix} 3x - 2y = 10& & \\ 3x -2y = 10 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y = \frac{3}{2}x-5& & \\ 0x=0 & & \end{matrix}\right.\) (Luôn đúng với mọi số thực x)

Vậy hệ có nghiệm là \(\left\{\begin{matrix} x\epsilon \mathbb{R}\\ y=\frac{3}{2}x-5 \end{matrix}\right.\)

Giải hệ phương trình sau:

\(\left\{\begin{matrix} (1 + \sqrt{2})x+ (1 - \sqrt{2})y = 5& & \\ (1 + \sqrt{2})x + (1 + \sqrt{2})y = 3& & \end{matrix}\right.\)

Phương pháp giải

• Trừ vế với vế của phương trình \((1)\) cho phương trình \((2)\) ta được phương trình bậc nhất một ấn (ẩn \(y\).)
• Giải phương trình một ẩn tìm được.
• Thay nghiệm của phương trình một ẩn trên vào phương trình \((1)\) rồi suy ra nghiệm của hệ.

Hướng dẫn giải

\(\Leftrightarrow \left\{\begin{matrix} (1 + \sqrt{2}x)+ (1 - \sqrt{2})y = 5& & \\ y(1-\sqrt{2}-1-\sqrt{2})=2& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} (1 + \sqrt{2}x)+ (1 - \sqrt{2})y = 5& & \\y=-\frac{\sqrt{2}}{2}& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix}x=\frac{-6+7\sqrt{2}}{2} & & \\y=-\frac{\sqrt{2}}{2}& & \end{matrix}\right.\)

Vậy nghiệm của hệ là \((x;y)=\left (\frac{-6+7\sqrt{2}}{2} ;-\frac{\sqrt{2}}{2} \right )\)

Giải hệ các phương trình:

a) \(\left\{\begin{matrix} 2(x + y)+ 3(x - y)=4 & & \\ (x + y)+2 (x - y)= 5& & \end{matrix}\right.\)

b) \(\left\{\begin{matrix} 2(x -2)+ 3(1+ y)=-2 & & \\ 3(x -2)-2 (1+ y)=-3& & \end{matrix}\right.\)

Phương pháp giải

Cách 1: Thực hiện nhân phá ngoặc thu gọn vế trái rồi áp dụng quy tắc cộng đại số để giải hệ phương trình.

Cách 2: Sử dụng phương pháp đặt ẩn phụ

• Đặt điều kiện (nếu có).
• Đặt ẩn phụ và điều kiện của ẩn (nếu có).
• Giải hệ phương trình theo các ẩn đã đặt.
• Thay kết quả tìm được vào ẩn ban đầu để tìm nghiệm của hệ.

Hướng dẫn giải

Câu a

\(\left\{\begin{matrix} 2(x + y)+ 3(x - y)=4 & & \\ (x + y)+2 (x - y)= 5& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 5x-y=4 & & \\ 3x-y= 5& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} y=5x-4 & & \\ 2x=-1& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} y=-\frac{13}{2} & & \\ x=-\frac{1}{2}& & \end{matrix}\right.\)

Vậy nghiệm của hệ là \((x;y)=\left (-\frac{1}{2};-\frac{13}{2} \right )\)

Câu b

\(\left\{\begin{matrix} 2(x -2)+ 3(1+ y)=-2 & & \\ 3(x -2)-2 (1+ y)=-3& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 2x+3y=-1 & & \\ 3x-2y=5& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 6x+9y=-3 & & \\ 6x-4y=10& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} 2x+3y=-1 & & \\ 13y=-13& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x=1 & & \\ y=-1& & \end{matrix}\right.\)

Vậy nghiệm của hệ là \((x;y)=(1;-1)\)

Ta biết rằng: Một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0. Hãy tìm các giá trị của m và n để đa thức sau (với biến số x) bằng đa thức 0: \(P(x) = (3m - 5n + 1)x + (4m - n -10)\).

Phương pháp giải

• Đa thức \(P(x)=ax+b =0 (đa\ thức\ 0) \Leftrightarrow \left\{ \begin{matrix} a=0 & & \\ b = 0 & & \end{matrix}\right.\).
• Giải hệ phương trình trên ta được giá trị cần tìm.

Hướng dẫn giải

Ta có 

\(P(x) = (3m - 5n + 1)x + (4m - n -10)\) có hai hệ số là \(a=(3m - 5n + 1)  \) và \(b=(4m - n -10)\).

Do đó \(P(x) = 0 \Leftrightarrow \left\{\begin{matrix} 3m - 5n +1 = 0 & & \\ 4m - n -10=0& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} 3m - 5n = -1 & & \\ 4m - n =10& & \end{matrix}\right.  \Leftrightarrow \left\{\begin{matrix} 3m - 5n = -1 & & \\ 20m - 5n =50& & \end{matrix}\right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}
3m - 5n - \left( {20m - 5n} \right) = - 1 - 50\\
4m - n = 10
\end{array} \right.\)

\(\Leftrightarrow \left\{\begin{matrix} -17m = -51 & & \\ 4m - n =10& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m = 3 & & \\ -n = 10 - 4.3& & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} m = 3 & & \\ n = 2& & \end{matrix}\right.\)

Vậy \(m=3,\ n=2\) thì đa thức \(P(x) =0\)

Xác định a và b để đồ thị của hàm số \(y = ax + b\) đi qua điểm A và B trong mỗi trường hợp sau:

a) \(A(2; -2)\) và \(B(-1; 3)\)

b) \(A(-4; -2)\) và \(B(2; 1)\)

c) \(A(3; -1)\) và \(B(-3; 2)\)

d) \(A(\sqrt{3}; 2)\) và \(B(0; 2)\)

Phương pháp giải

Xác định \(a,\ b\) để đồ thị hàm số \(y=ax+b\) đi qua hai điểm \(A,\ B\).

• Lần lượt thay tọa độ của \(A,\ B\) vào \(y=ax+b\) thì được hệ phương trình bậc nhất hai ẩn \(a,\ b\).
• Giải hệ phương trình này, ta tìm được \(a,\ b\).

Hướng dẫn giải

Câu a

\(\Leftrightarrow \left\{\begin{matrix} 2a + b = -2 & & \\ 3a = -5& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} b=\frac{4}{3} & & \\ a = -\frac{5}{3}& & \end{matrix}\right.\)

Vậy \(a=-\frac{5}{3};b=\frac{4}{3}\) thỏa bài toán

Câu b

\(\Leftrightarrow \left\{\begin{matrix} -4a + b = -2 & & \\ 6a = 3& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} b = 0 & & \\ a = \frac{1}{2}& & \end{matrix}\right.\)

Vậy \(a=\frac{1}{2};b=0\) thỏa bài toán

Câu c

\(\Leftrightarrow \left\{\begin{matrix} 3a + b = -1 & & \\ 2b = 1& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} a=-\frac{1}{2} & & \\ b = \frac{1}{2}& & \end{matrix}\right.\)

Vậy \(a=-\frac{1}{2};b=\frac{1}{2}\) thỏa bài toán

Câu d

\(\left\{\begin{matrix} a\sqrt{3} + b =2 & & \\ 0. a + b = 2& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} a\sqrt{3} + b =2 & & \\ b = 2& & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} a=0 & & \\ b = 2& & \end{matrix}\right.\)

Vậy \(a=0;b=2\) thỏa bài toán

Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về  dạng hệ hai phương trình bậc nhật hai ẩn rồi giải:

a) \(\left\{\begin{matrix} \frac{1}{x} - \frac{1}{y} = 1& & \\ \frac{3}{x} + \frac{4}{y} = 5& & \end{matrix}\right.\). Hướng dẫn. Đặt \(u=\frac{1}{x};v=\frac{1}{y}\)

b) \(\left\{\begin{matrix} \frac{1}{x - 2} + \frac{1}{y -1} = 2 & & \\ \frac{2}{x - 2} - \frac{3}{y - 1} = 1 & & \end{matrix}\right.\). Hướng dẫn. Đặt \(u=\frac{1}{x-2};v=\frac{1}{y-1}\)

Phương pháp giải

Phương pháp đặt ẩn phụ:

• Đặt điều kiện (nếu có)
• Đặt ẩn phụ và điều kiện của ẩn phụ (nếu có).
• Giải hệ phương trình theo các ẩn phụ đã đặt.
• Trở lại ẩn ban đầu để tìm nghiệm của hệ.

Hướng dẫn giải

Câu a

Điều kiện: \(x \neq 0;y \neq 0\)

Đặt \(u=\frac{1}{x};v=\frac{1}{y}\), ta được hệ mới là:

\(\left\{\begin{matrix} u-v=1\\ 3u+4v=5 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=1+v\\ 3(1+v)+4v=5 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=1+v\\ 7v=2 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u=\frac{9}{7}\\ v=\frac{2}{7} \end{matrix}\right.\)

\(u=\frac{9}{7}\Rightarrow x=\frac{7}{9}\)

\(v=\frac{2}{7}\Rightarrow y=\frac{7}{2}\)

Vậy nghiệm của hệ là \((x;y)=\left (\frac{7}{9};\frac{7}{2} \right )\)

Câu b

Điều kiện: \(x \neq 2;y \neq 1\)

Đặt \(u=\frac{1}{x-2};v=\frac{1}{y-1}\), ta được hệ mới là:

\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ 2u - 3v = 1 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ 2(2-v) - 3v = 1 & & \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} u = 2-v & & \\ -5v = -3 & & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} u = \frac{7}{5} & & \\ v = \frac{3}{5} & & \end{matrix}\right.\)

\(u=\frac{7}{5}\Rightarrow \frac{1}{x-2}=\frac{7}{5}\Leftrightarrow x=\frac{19}{7}\)

\(v=\frac{3}{5}\Rightarrow \frac{1}{y-1}=\frac{3}{5}\Leftrightarrow y=\frac{8}{3}\)

Vậy nghiệm của hệ là \((x;y)=\left (\frac{19}{7};\frac{8}{3} \right )\)