Giải bài tập SGK Toán 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông

Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng $34^{\circ}$ và bóng của một tháp trên mặt đất dài $86m$ (H.30). Tính chiều cao của tháp (làm tròn đến mét).

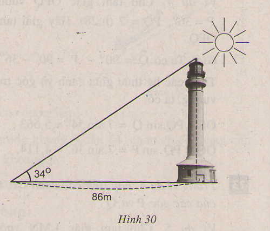
Phương pháp giải

• Tháp đặt vuông góc với mặt đất nên ta có tam giác vuông.
• Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $A$ thì: $AC=AB. \tan B = AB. \cot C$ 

Hướng dẫn giải

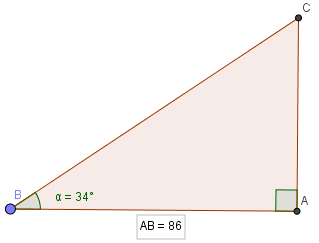
Xét tam giác $ABC$ vuông tại $A$, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

$\tan B = \dfrac{AC}{AB} \Leftrightarrow \tan 34^o = \dfrac{AC}{86}$

$\Leftrightarrow AC = 86. \tan 34^o \approx 58 (m)$

Vậy chiều cao của tháp là: $58 \left ( m \right )$.

Giải tam giác ABC vuông tại A, biết rằng

a) $b=10cm; \widehat{C}=30^{\circ}$

b) $c=10cm; \widehat{C}=45^{\circ}$

c) $a=20cm; \widehat{B}=35^{\circ}$ 

d) $c = 21cm; b = 18cm$

Phương pháp giải

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác $ABC$ vuông tại $A$ thì

 $b=a.\sin B = a . \cos C;$                  $b = c. \tan B = c. \cot C;$

$c=a.\sin C = a. \cos B;$                    $c=b.\tan C = b.\cot B$.  

Hướng dẫn giải

Câu a

$b=10cm; \widehat{C}=30^{\circ}$

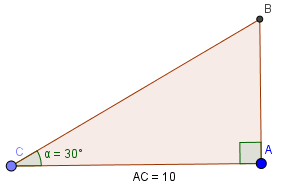
$\widehat{B}=90^{\circ}-30^{\circ}=60^{\circ}$

$AB=AC.tanC=10.tan30^{\circ}\approx 5,774 (cm)$

$BC = \frac{{AC}}{{{\rm{cosC}}}} = \frac{{10}}{{{\rm{cos3}}{{\rm{0}}^ \circ }}} \approx 11,547(cm)$

Câu b

$c=10cm; \widehat{C}=45^{\circ}$

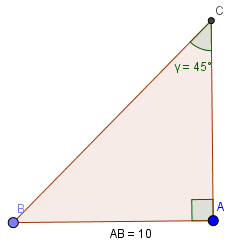
Lưu ý: Tam giác vuông có một góc bằng 45 độ thì tam giác đó vuông cân!

$\Rightarrow \widehat{B}=45^{\circ}$

$\Rightarrow AC=AB=10 (cm)$

$BC=\frac{AB}{sin C}=\frac{10}{\sin45^{\circ}}=10\sqrt{2}\approx 14,142 (cm)$

Câu c

$a=20cm; \widehat{B}=35^{\circ}$ 

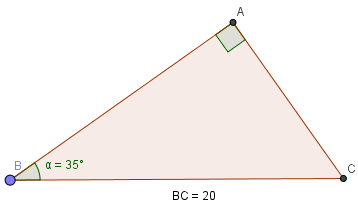
$\widehat{C}=90^{\circ}-35^{\circ}=55^{\circ}$

$AB=BCcosB=20cos35^{\circ}\approx 16,383 (cm)$

$AC= BCsinB=20sin35^{\circ}\approx 11,472 (cm)$

Câu d

c = 21cm; b = 18cm

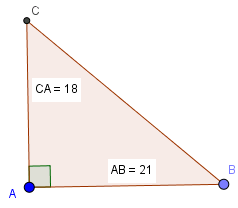
$tanB=\frac{AC}{AB}=\frac{18}{21}\approx 0,857$

$\Rightarrow \left\{\begin{matrix} \widehat{B}\approx 41^{\circ}\\ \widehat{C }\approx 49^{\circ} \end{matrix}\right.$

$BC = \frac{{AC}}{{{\rm{sinB}}}} = \frac{{18}}{{{\rm{sin4}}{{\rm{1}}^ \circ }}} \approx 27,437(cm)$

Nếu tính BC theo định lý Pytago thì

$BC = \sqrt {{{21}^2} + {{18}^2}}  \approx 27,659(cm)$

Kết quả này chính xác hơn vì khi tính toán, ta dùng ngay các số liệu đã cho mà không dùng kết quả trung gian (vì ở trên, góc B đã được làm tròn)

Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc $\alpha$ trong hình 31).

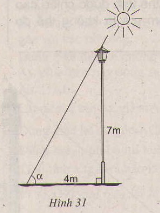
Phương pháp giải

• Dựng tam giác có các cạnh và góc thỏa mãn đề bài.
• Sử dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông $\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề}.$ Từ đó dùng máy tính tính được độ lớn góc $\alpha$.

Hướng dẫn giải

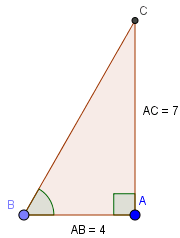
Xét tam giác $ABC$ vuông tại $A$ có $AC=7m,\ AB = 4m,\ \widehat{B}=\alpha .$ Ta cần tính góc $B$.

Theo định nghĩa tỷ số lượng giác của góc nhọn trong tam giác vuông, ta có:

$\tan \alpha = \tan B =\dfrac{AC}{AB}=\dfrac{7}{4} =1,75.$

Bấm máy tính ta được: $\alpha \approx 60^o 15'.$

Một khúc sông rộng khoảng $250m$. Một chiếc thuyền chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu độ? (góc $\alpha$ trong hình 32).

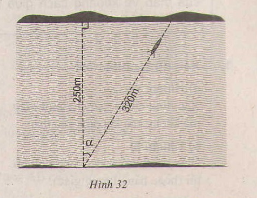
Phương pháp giải

• Dựng tam giác có các cạnh và góc thỏa mãn đề bài.
• Sử dụng định nghĩa tỉ số lượng giác của góc nhọn: $\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}.$ Từ đó dùng máy tính tính được số đo góc $\alpha$. 

Hướng dẫn giải

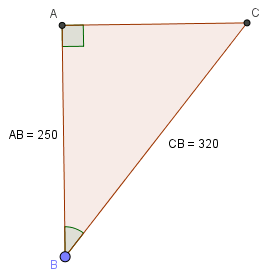
Xét tam giác $ABC$ vuông tại $A$ có $AB=250m,\ BC=320m$. Ta cần tính góc $B$.

Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

$\cos \alpha =\cos B =\dfrac{AB}{BC}=\dfrac{250}{320}=0,78125.$

$\Rightarrow \alpha \approx 38^{\circ}37'$.

Vậy chiếc đò lệch đi một góc gần bằng: $38^{\circ}37'$. 

Cho tam giác ABC, trong đó BC=11cm, $\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}.$ Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính:

a) Đoạn thẳng AN

b) Cạnh AC

Gợi ý: Kẻ BK vuông góc với AC.

Phương pháp giải

- Tam giác $ABC$ vuông tại $A$ thì $\widehat{B}+\widehat{C}=90^o$.

- Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác $ABC$ vuông tại $A$ thì

• $b=a.\sin B \Rightarrow a=\dfrac{b}{\sin B}$
• $b= a . \cos C \Rightarrow a=\dfrac{b}{\cos C}$

Hướng dẫn giải

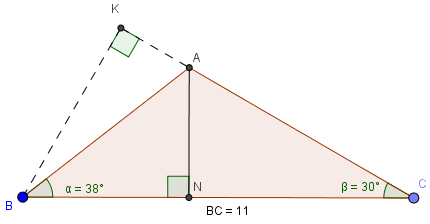
Câu a

Dựng  tại K

Ta có

$\widehat{KBC}=90^o-\widehat{ACB}=60^o$

$\widehat{KBA}=\widehat{KBC}-\widehat{ABC}=60^o-38^o=22^o$

Xét tam giác KBC vuông tại K ta có:

$BK=BCsinC=11sin30^{\circ}=5,5(cm)$

Xét tam giác KBA vuông tại K ta có: 

$AB=\frac{BK}{cos22^{\circ}}=\frac{5,5}{\cos22^{\circ}}\approx 5,932 (cm)$

Xét tam giác ABN vuông tại N ta có:

$AN= ABsin38^{\circ}\approx 5,932sin38^{\circ}\approx 3,652(cm)$

Câu b

Xét tam giác ANC vuông tại N ta có:

$AC=\frac{AN}{sin C}=\frac{3,652}{sin30^{\circ}}\approx 7,304(cm)$

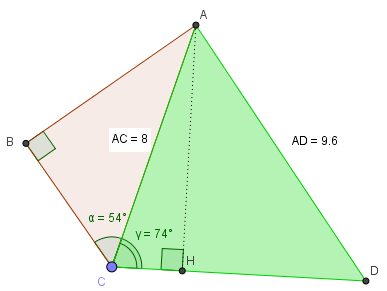
Trong hình 33

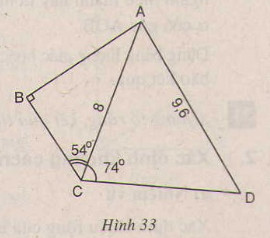
$AC=8cm, AD=9,6cm, \widehat{ABC}=90^{\circ}, \widehat{ACD}=74^{\circ}.$

Hãy tính

a) AB

b) $\widehat {ADC}$

Phương pháp giải

a) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $B$ thì: $AB=AC. \sin C$.

b) Kẻ thêm đường cao để làm xuất hiện tam giác vuông (Kẻ $AH ⊥ CD$)

• Sử dụng hệ thức về cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $A$ khi đó: $AB=BC. \sin C$ hoặc $AC=AB. \sin B$.
• Biết $\sin \alpha$ dùng máy tính ta tính được số đo góc $\alpha$.

Hướng dẫn giải

Câu a

Xét tam giác ABC vuông tại B có:

 $AB=ACsinC=8sin 54^{\circ}\approx 6,472(cm)$

Câu b

Dựng $AH\perp CD$ tại H (H thuộc CD)

Xét tam giác ACH vuông tại H có:

 $AH=ACsinC=8sin74^{\circ}\approx 7,690(cm)$

Xét tam giác AHD vuông tại H có:

$\begin{array}{l} \sin D = \frac{{AH}}{{AD}} \approx \frac{{7,690}}{{9,6}} \approx 0,8010\\  \Rightarrow \widehat D \approx {53^ \circ } \end{array}$

Một con thuyền với vận tốc $2km/h$ vượt qua một khúc sông nước chảy mạnh mất $5$ phút. Biết rằng đường đi của con thuyền tạo với bờ một góc $70^{\circ}$. Từ đó đã có thể tính được chiều rộng của khúc sông chưa? Nếu có thể hãy tính kết quả (làm tròn đến mét). 

Phương pháp giải

• Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông: $\Delta{ABC}$ vuông tại $A$, khi đó:$AB=BC. \sin C;$    $AC=BC.\sin B$. 
• Công thức liên hệ giữa quãng đường $(S)$, vận tốc $(v)$ và thời gian $(t)$ là: $S=v.t$.

Hướng dẫn giải

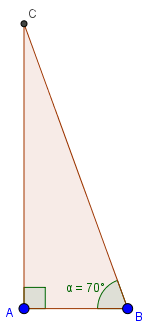
Xét tam giác ABC vuông tại A có góc B bằng 70 độ:

Gọi BC là đoạn đường con thuyền đi được trong 5 phút, AC là chiều rộng khúc sông.

Quãng đường thuyền đi được trong 5 phút bằng $\frac{1}{12}$ giờ là:

$BC=2.\frac{1}{12}=\frac{1}{6}(km)\approx 166,67(m)$

Chiều rộng AC của khúc sông là

$AC=BCsin\widehat{ABC}=166,67.sin70^o\approx 156,6(m)$