Giải bài tập SGK Toán 9 Bài: Luyện tập

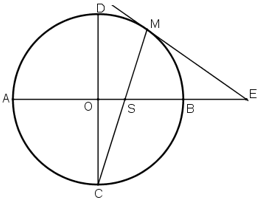
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES = EM.

Phương pháp giải

Để chứng minh  \(SE =EM\) ta cần chứng minh tam giác SEM cân tại E. 

Hướng dẫn giải

Vì AB và CD là hai đường kính vuông góc với nhau nên \( \overset\frown{AC}=\overset\frown{BC}=\overset\frown{BD}=\overset\frown{AD} \)

Ta có: \(\widehat{ESM}\)  là góc có đỉnh ở bên trong đường tròn nên 

\(\widehat{MSE}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AC}+\text{sđ}\overset\frown{MB} \right) \)

\(\widehat{CME}\)  là góc tạo bởi tia tiếp tuyến và dây cung nên

\( \begin{aligned} \widehat{CME}&=\dfrac{1}{2}.\text{sđ}\overset\frown{CBM} \\ & =\dfrac{1}{2}.\left( \text{sđ}\overset\frown{CB}+\text{sđ}\overset\frown{BM} \right) \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{AC}+\text{sđ}\overset\frown{BM} \right)=\widehat{MSE} \\ \end{aligned}\)

Vậy \(\widehat{MSE}=\widehat{SME} \) hay tam giác SEM cân tại E

Suy ra \(SE =EM\)

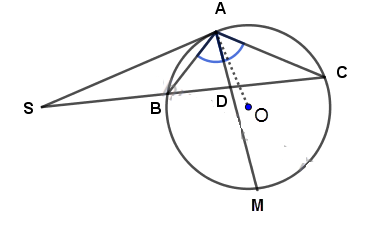
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyến SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh \(SA = SD.\)

Phương pháp giải

Chứng minh \(\widehat{SAD}=\widehat{SDA}\)

Áp dụng định lý góc có đỉnh ở bên trong đường tròn.

Gọi M là giao điểm của AD và đường tròn (O)

\(\widehat{ADB} \)  là có đỉnh ở bên trong đường tròn nên \(\widehat{ADB}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{MC} \right) \)

\(\widehat{SAD} \)  là góc tạo bởi tia tiếp tuyến và dây cung nên 

\(\widehat{SAD}=\dfrac{1}{2}.\text{sđ}\overset\frown{ABM}\)

Hướng dẫn giải

Gọi M là giao điểm của AD và đường tròn (O)

Có \( \widehat{BAC}\)  là góc nội tiếp chắn cung BC.

AM là phân giác của \(\widehat{BAC}\) nên

 \(\widehat{BAM}=\widehat{CAM}\Rightarrow \overset\frown{BM}=\overset\frown{CM}\) (trong một đường tròn, hai góc nội tiếp bằng nhau chắn các cung bằng nhau)

Xét đường tròn (O) có:

\(\widehat{ADB} \)  là có đỉnh ở bên trong đường tròn nên \(\widehat{ADB}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{MC} \right) \)

\(\widehat{SAD} \)  là góc tạo bởi tia tiếp tuyến và dây cung nên 

\( \begin{aligned} \widehat{SAD}&=\dfrac{1}{2}.\text{sđ}\overset\frown{ABM} \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{BM} \right) \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{MC} \right) \\ & =\widehat{ADS} \\ \end{aligned} \)

Vậy tam giác SAD cân tại S. Suy ra \(SA=SD.\)

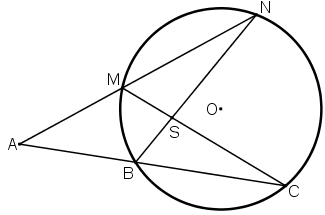
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn. Chứng minh \(\widehat{A}+\widehat{BSM}=2.\widehat{CMN}\)

Phương pháp giải

Ta chứng minh:

\(\widehat{BSM}\)  là góc có đỉnh ở bên trong đường tròn nên

\(\widehat{BSM}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{CN} \right) \)

\(\widehat{A} \) là góc có đỉnh nằm ngoài đường tròn nên 

\(\widehat{A}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CN}-\text{sđ}\overset\frown{BM} \right) \)

suy ra: \(\widehat{A}+\widehat{BSM}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CN}-\text{sđ}\overset\frown{BM} \right)+\dfrac{1}{2}\left( \text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{CN} \right)\)

Hướng dẫn giải

Trong đường tròn (O) có

\(\widehat{CMN} \) là góc nội tiếp chắn cung CN nên \(\widehat{CMN}=\dfrac{1}{2}\text{sđ}\overset\frown{CN} \)

\(\widehat{BSM}\)  là góc có đỉnh ở bên trong đường tròn nên

\(\widehat{BSM}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{CN} \right) \)

\(\widehat{A} \) là góc có đỉnh nằm ngoài đường tròn nên 

\(\widehat{A}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CN}-\text{sđ}\overset\frown{BM} \right) \)

Ta có:

\( \begin{aligned} \widehat{A}+\widehat{BSM}&=\dfrac{1}{2}\left( \text{sđ}\overset\frown{CN}-\text{sđ}\overset\frown{BM} \right)+\dfrac{1}{2}\left( \text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{CN} \right) \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{CN}-\text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{BM}+\text{sđ}\overset\frown{CN} \right) \\ & =2.\dfrac{1}{2}\text{sđ}\overset\frown{CN}=2\widehat{CMN} \\ \end{aligned} \)

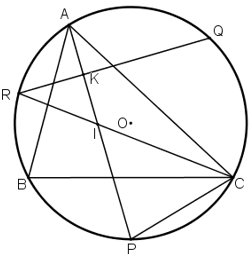
Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.

a) Chứng minh \(AP\bot QP\)

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Phương pháp giải

a) Chứng minh:

\(\widehat{AKR}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\widehat{PCQ} \right)\\ \widehat{AKQ}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AQ}+\text{sđ}\overset\frown{RBP} \right)\)

Suy ra: \( \begin{aligned} \widehat{AKQ}=\widehat{AKR} \\ \end{aligned}\)

Mà: \(\widehat{AKR}+\widehat{AKQ}={{180}^{o}}\)

Vậy ta có điều cần phải chứng minh

b) Chứng minh: \(\begin{aligned} & \widehat{PIC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\overset\frown{PC} \right) \\ \end{aligned} \)

Hướng dẫn giải

a) Vì P, Q, R lần lượt là các điểm chính giữa của các cung BC, AC, AB nên ta có: 

\(\overset\frown{AR}=\overset\frown{RB};\overset\frown{AQ}=\overset\frown{QC};\overset\frown{BP}=\overset\frown{PC} \)

Gọi K là giao điểm của AP và QR.

Ta có:

\(\widehat{AKR}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\widehat{PCQ} \right)\\=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\overset\frown{PC}+\text{sđ}\overset\frown{QC} \right)\\ \widehat{AKQ}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AQ}+\text{sđ}\overset\frown{RBP} \right)\\=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AQ}+\text{sđ}\overset\frown{RB}+\text{sđ}\overset\frown{BP} \right) \)

Mà \( \overset\frown{AR}=\overset\frown{RB};\overset\frown{AQ}=\overset\frown{QC};\overset\frown{BP}=\overset\frown{PC}\)

 Nên ta có:

\( \begin{aligned} \widehat{AKQ}&=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AQ}+\text{sđ}\overset\frown{RBP} \right) \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{AQ}+\text{sđ}\overset\frown{RB}+\text{sđ}\overset\frown{BP} \right) \\ & =\dfrac{1}{2}\left( \text{sđ}\overset\frown{QC}+\text{sđ}\overset\frown{AR}+\text{sđ}PC \right) \\ & =\widehat{AKR} \\ \end{aligned}\)

Lại có 

\(\begin{aligned} & \widehat{AKR}+\widehat{AKQ}={{180}^{o}} \\ & \Rightarrow 2\widehat{AKR}={{180}^{o}} \\ & \Rightarrow \widehat{AKR}={{90}^{o}} \\ & \Rightarrow AP\bot RQ \\ \end{aligned} \)

 b)  Ta có:

\(\begin{aligned} & \widehat{PIC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\overset\frown{PC} \right) \\ & \widehat{PCI}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{RBP} \right)=\dfrac{1}{2}\left( \text{sđ}\overset\frown{RB}+\text{sđ}\overset\frown{BP} \right)\\&=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AR}+\text{sđ}\overset\frown{BC} \right)=\widehat{PIC} \\ \end{aligned} \)

 Vậy CPI cân tại P.

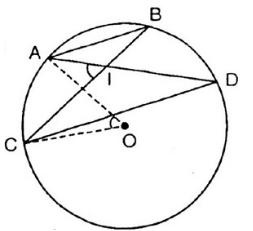
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I.

Chứng minh: \(\widehat{AOC}=\widehat{AIC}\)

Phương pháp giải

Biểu diễn số đo góc AIC và góc AOC theo số đo cung AC

Hướng dẫn giải

Ta có:

\(\overset\frown{AC}=\overset\frown{BC}\) (hai cung bị chắn bởi hai dây song song)

\(\widehat{AIC}\)  là góc có đỉnh ở bên trong đường tròn nên:

\(\widehat{AIC}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AC}+\text{sđ}\overset\frown{BD} \right)=\dfrac{1}{2}.2\text{sđ}\overset\frown{AC}=\text{sđ}\overset\frown{AC} \)

\(\widehat{AOC} \) là góc ở tâm nên \(\widehat{AOC}=\text{sđ}\overset\frown{AC} \)

Do đo: \(\widehat{AIC}=\widehat{AOC} \)