Giải bài tập SGK Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Phần hướng dẫn giải bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
Mục lục nội dung
1. Giải bài 1 trang 68 SGK Toán 9 tập 1
2. Giải bài 2 trang 68 SGK Toán 9 tập 1
3. Giải bài 3 trang 69 SGK Toán 9 tập 1
4. Giải bài 4 trang 69 SGK Toán 9 tập 1
5. Giải bài 5 trang 69 SGK Toán 9 tập 1
6. Giải bài 6 trang 69 SGK Toán 9 tập 1
7. Giải bài 7 trang 69 SGK Toán 9 tập 1

1. Giải bài 1 trang 68 SGK Toán 9 tập 1
Hãy tính x và y trong mỗi hình sau (hình 4a, b)
.png)
Phương pháp giải
- Sử dụng định lí Pytago trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), khi đó: \(BC^2=AC^2+AB^2\).
- Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền: \(b^2=a.b',\ c^2=a.c'\)
Hướng dẫn giải
Câu a
Đặt tên các đỉnh của tam giác như hình sau:
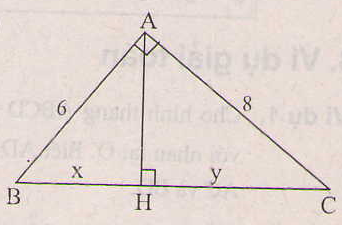
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH
\(AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6\)
\(HC=BC=BH=10-3,6=6,4\)
Câu b
Ta vẽ hình và đặt tên thích hợp:
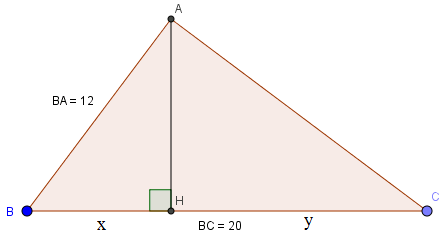
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH, ta có:
\(AB^2=BH.BC=20.x\Rightarrow x=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\)
\(HC=BC-BH=20-7,2=12,8\)
2. Giải bài 2 trang 68 SGK Toán 9 tập 1
Hãy tính x và y trong hình dưới đây
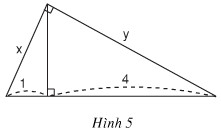
Phương pháp giải
- Tính độ dài cạnh huyền.
- Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền. Biết hình chiếu và cạnh huyền ta tính được cạnh góc vuông. \(b^2=a.b',\ c^2=a.c'\)
Hướng dẫn giải
Nhận thấy rằng, cạnh huyền có độ lớn là: \(1+4=5\)
Áp dụng hệ thức lượng trong tam giác vuông đó là bình phương cạnh góc vuông bằng cạnh huyền nhân hình chiếu của cạnh ấy trên cạnh huyền, ta được:
\(x^2=1.5\Leftrightarrow x=\sqrt{5}\)
\(y^2=5.4\Leftrightarrow y=2\sqrt{5}\)
3. Giải bài 3 trang 69 SGK Toán 9 tập 1
Hãy tính x và y trong hình sau (h.6)
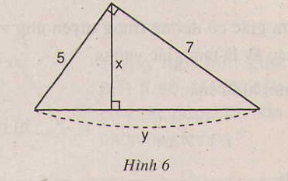
Phương pháp giải
- Sử dụng định lí Pytago để tính cạnh huyền.
- Sử dụng hệ thức liên quan đến đường cao để tính đường cao: \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\)
- Hoặc sử dụng công thức: \(b.c = h.a\)
Hướng dẫn giải
Ta có y có vai trò là cạnh huyền của tam giác vuông nên: \(y=\sqrt{5^2+7^2}=\sqrt{74}\)
Áp dụng công thức tính đường cao trong tam giác vuông, ta có
\(\frac{1}{x^2}=\frac{1}{5^2}+\frac{1}{7^2}\)
\(\Rightarrow x=\sqrt{\frac{5^2.7^2}{5^2+7^2}}=\frac{35\sqrt{74}}{74}\)
4. Giải bài 4 trang 69 SGK Toán 9 tập 1
Hãy tính x và y trong hình sau
.png)
Phương pháp giải
- Sử dụng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\). Biết \(h,\ c'\) tính được \(b'\).
- Tính độ dài cạnh huyền: \(a=b'+c'\).
- Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a\). Biết \(a,\ b'\) tính được \(b\).
Hướng dẫn giải
Đặt tên như trong hình vẽ, áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có
\(AH=\sqrt{1^2+2^2}=\sqrt{5}\)
Áp dụng hệ thức lượng trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền và hình chiếu, ta có
\(AH^2=BH.BC\Leftrightarrow (\sqrt{5})^2=1.(1+x)\)
\(\Rightarrow x=4\)
Áp dụng định lí Pytago vào tam giác AHC vuông tại H, ta có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
5. Giải bài 5 trang 69 SGK Toán 9 tập 1
Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền
Phương pháp giải
- Dùng định lí Pytago để tính cạnh huyền.
- Dùng hệ thức \(h.a=b.c\). Biết hai cạnh góc vuông \(b,\ c\) và cạnh huyền \(a\) tính được đường cao \(h\).
- Biết cạnh huyền \(a\) và các cạnh góc vuông \(a,\ c\). Dùng các hệ thức \(b^2=b'.a\); \(c^2=c'.a\) suy ra \(b' =\dfrac{b^2}{a};\ c'=\dfrac{c^2}{a}\).
Hướng dẫn giải
.png)
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)
Áp dụng hệ thức lượng vào các tam giác ABC vuông tại A, AHB vuông tại H, AHC vuông tại H, ta có:
\(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4\)
\(AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{3^2}{5}=1,8\)
\(CH=BC-BH=5-1,8=3,2\)
6. Giải bài 6 trang 69 SGK Toán 9 tập 1
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.
Phương pháp giải
- Tính cạnh huyền: \(a=b' +c'\).
- Dùng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a;\ c^2=c'.a\), biết hình chiếu \(b',\ c'\) và cạnh huyền \(a\), tính được \(a,\ b\).
Hướng dẫn giải
.png)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH, ta có:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{1.2}=\sqrt{2}\)
Áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có:
\(AH=\sqrt{BH^2+AH^2}=\sqrt{1+2}=\sqrt{3}\)
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{3^2-3}=\sqrt{6}\)
7. Giải bài 7 trang 69 SGK Toán 9 tập 1
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2 = ab) như trong hai hình sau:
.png)
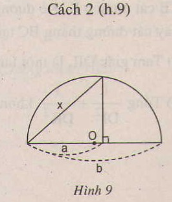
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông
Phương pháp giải
- Đặt tên các điểm và nối các điểm lại để xuất hiện tam giác.
- Dùng dấu hiệu: "tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó là tam giác vuông" để chứng minh tam giác vuông.
- Dùng các hệ thức sau để chứng minh \(x\) là trung bình nhân của \(a,\ b\)
- \(b^2=a.b',\ c^2=a.c'\) \((1)\)
- \(h^2=b'.c'\) \((2)\)
- Nêu các bước để vẽ được đoạn trung bình nhân.
Hướng dẫn giải
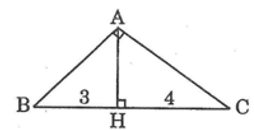
Giả sử tam giác ABC có góc BAC = 90o, AH ⊥ BC, BH = 3, CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC = 3.(3 + 4) = 3.7 = 21 ⇒ AB = √21
AC2 = CH.BC = 4.(3 + 4) = 4.7 = 28 ⇒ AC = √28 = 2√7
8. Giải bài 8 trang 70 SGK Toán 9 tập 1
Tìm x và y trong mỗi hình sau
.png)
.png)
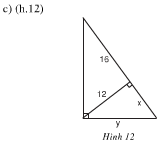
Phương pháp giải
Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(b',\ c'\) tính được \(h\).
Dùng hệ thức liên quan đến đường cao và hai cạnh góc vuông \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\) để tính \(y\).
Dùng định lí Pytago trong tam giác vuông để tính \(x\).
Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(h,\ b'\) tính được \(c'\).
Dùng định lí Pytago trong tam giác vuông.
Hướng dẫn giải
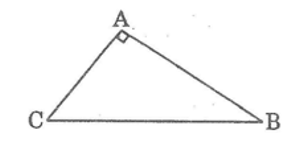
Giả sử tam giác ABC có góc (BAC) = 900
Theo đề bài, ta có: BC – AB = 1 (cm) (1)
AB + AC – BC = 4 (cm) (2)
Từ (1) và (2) suy ra: BC – AB + AB + AC – BC = 4 + 1 = 5 (cm)
Theo định lí Pi-ta-go, ta có: BC2 = AB2 + AC2 (3)
Từ (1) suy ra: BC = AB + 1 (4)
Thay (4) vào (3) ta có
(AB + 1)2 = AB2 + AC2
⇔ AB2 + 2AB + 1 = AB2 + 52
⇔ 2AB = 24 ⇔ AB = 12 (cm)
Thay AB = 12 (cm) vào (1) ta có: BC = 12 + 1 = 13 (cm)
9. Giải bài 9 trang 70 SGK Toán 9 tập 1
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và Tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng
a) Tam giác DIL là một tam giác cân
b) Tổng \(\frac{1}{{D{I^2}}} + \frac{1}{{D{K^2}}}\) không đổi khi I thay đổi trên cạnh AB
Phương pháp giải
a) Chứng minh hai tam giác bằng nhau\((\Delta{ADI}\) và \(\Delta{CDL})\) từ đó suy ra hai cạnh tương ứng bằng nhau.
b) Sử dụng hệ thức lượng trong tam giác vuông: \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\) để đưa tổng đã cho về tổng của các số không đổi.
Hướng dẫn giải
câu a: Ta có: \(\widehat{ADI}=\widehat{IKB}\) (so le trong)
\(\widehat{CDL}=\widehat{IKB}\) (vì cùng phụ với góc L)
Vậy \(\widehat{CDL}=\widehat{ADI}\)
Xét hai tam giác vuông IAD và LCD có:
\(\widehat{IAD}=\widehat{LCD}=90^o\)
\(AD=CD\)
\(\widehat{CDL}=\widehat{ADI}\)
Vậy \(\Delta IAD=\Delta LCD (g.c.g)\)
\(\Rightarrow ID=DL\)
Vậy tam giác DIL vuông tại D
Câu b: Ta có
\(DI=DL\Rightarrow \frac{1}{DI^2}=\frac{1}{DL^2}\)
Xét tam giác DKL vuông tại D có đường cao DC, ta có:
\(\frac{1}{CD^2}=\frac{1}{DL^2}+\frac{1}{DK^2}\)
Theo cmt, ta viết lại là:
\(\frac{1}{CD^2}=\frac{1}{DI^2}+\frac{1}{DK^2}\)
Mà hình vuông ABCD cố định nên CD không đổi, vậy:
\(\frac{1}{DI^2}+\frac{1}{DK^2}\) luôn không đổi khi I thay đổi trên AB!
