Giải bài tập SGK Toán 9 Bài: Luyện tập

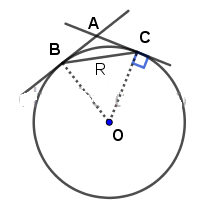
Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính $\widehat{ABC},\widehat{BAC}$.

Phương pháp giải

- Xét tam giác OBC là tam giác đều vì $OB=OC=BC=R$

Tìm số đo các góc: $\widehat{BOC}$, $\widehat{ABC}, \widehat{ACB}$

- Xét tam giác ABC, áp dụng định lý tổng ba góc trong tam giác tìm góc $\widehat{BAC}$

Hướng dẫn giải

Tam giác OBC là tam giác đều vì $OB=OC=BC=R$

Suy ra $\widehat{BOC}={{60}^{o}}\Rightarrow \text{sđ}\overset\frown{BC}={{60}^{o}}$

Ta có:

$\widehat{ABC}$  là góc tạo bởi tia tiếp tuyến và dây cung chắn cung bC nên:

$\widehat{ABC}=\dfrac{1}{2}\text{sđ}\overset\frown{BC}=\dfrac{1}{2}{{.60}^{o}}={{30}^{o}}$

Tương tự, ta cũng có: $\widehat{ACB}$  là góc tạo bởi tia tiếp tuyến và dây cung chắn cung bC nên:

$\widehat{ACB}=\dfrac{1}{2}\text{sđ}\overset\frown{BC}=\dfrac{1}{2}{{.60}^{o}}={{30}^{o}}$

Trong tam giác ABC, áp dụng định lý tổng ba góc trong tam giác ta có:

$\begin{aligned} & \widehat{ABC}+\widehat{BAC}+\widehat{ACB}={{180}^{o}} \\ & \Leftrightarrow {{30}^{o}}+\widehat{BAC}+{{30}^{o}}={{180}^{o}} \\ & \Leftrightarrow \widehat{BAC}={{120}^{o}} \\ \end{aligned}$

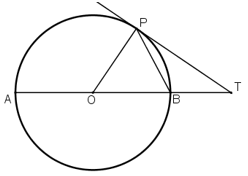
Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T).

Chứng minh $\widehat{BTP}+2\widehat{TPB}=90^o$

Phương pháp giải

Chứng minh

* $\widehat{PTO}+\widehat{POT}={{90}^{o}} (1)$

*$\begin{aligned} & \widehat{BPT}=\dfrac{1}{2}\text{sđ}\overset\frown{BP}=\dfrac{1}{2}\widehat{BOP} \\ & \Rightarrow \widehat{BOP}=2\widehat{BPT} \\ \end{aligned} (2)$

Từ (1) và (2) ta được điều cần chứng minh

Hướng dẫn giải

Vì PT là tiếp tuyến của đường tròn (O) tại P nên $\widehat{OPT}={{90}^{o}}$

Suy ra $\widehat{PTO}+\widehat{POT}={{90}^{o}} (1)$

Xét đường tròn O ta có:

$\widehat{TPB}$  là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BP nên 

$\begin{aligned} & \widehat{BPT}=\dfrac{1}{2}\text{sđ}\overset\frown{BP}=\dfrac{1}{2}\widehat{BOP} \\ & \Rightarrow \widehat{BOP}=2\widehat{BPT} \\ \end{aligned} (2)$

Từ (1) và (2) ta có:

$\widehat{BTP}+2\widehat{TPB}={{90}^{o}}$

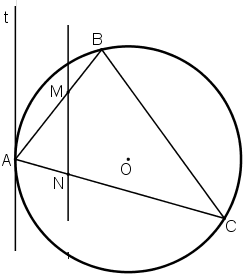
Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh $AB.AM = AC.AN.$

Phương pháp giải

- Chứng minh $\widehat{AMN}=\widehat{ACB}$

- Xét $\Delta ABC$  và $\Delta ANM$ chứng minh $\Delta ABC\backsim \Delta ANM\,\,(g.g)$

- Suy ra tỉ số đồng dạng $\dfrac{AB}{AN}=\dfrac{AC}{AM}$ từ đó ta được điều cần chứng minh.

Hướng dẫn giải

Xét đường tròn (O) có:

$\widehat{tAB}=\widehat{ACB}$ (góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AB)

Lại có $MN//tt’$ nên $\widehat{tAB}=\widehat{AMN}$ (hai góc so le trong)

Suy ra $\widehat{AMN}=\widehat{ACB}$

Xét $\Delta ABC$  và $\Delta ANM$ có:

+) $\widehat{A}$ chung

+) $\widehat{AMN}=\widehat{ACB}$

Suy ra $\Delta ABC\backsim \Delta ANM\,\,(g.g)$

Có: $\dfrac{AB}{AN}=\dfrac{AC}{AM}\Rightarrow AB.AM=AC.AN$ (cặp cạnh tương ứng tỉ lệ)

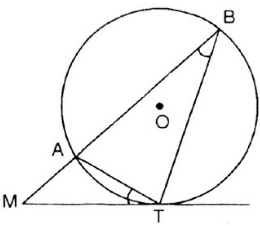
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.

Phương pháp giải

Chứng minh $\Delta MAT\backsim \Delta MTB$

Suy ra tỉ số đồng dạng: $\dfrac{MT}{MB}=\dfrac{MA}{MT}$ từ đó ta được điều phái chứng minh

Hướng dẫn giải

Trong đường tròn (O) có:

$\widehat{MTA}=\widehat{MBT}$ (góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AT)

Xét $\Delta MAT$  và $\Delta MTB$  có:

+) $\widehat{MTA}=\widehat{MBT}$

+) $\widehat{M}$  chung.

Suy ra $\Delta MAT\backsim \Delta MTB\,\,(g.g)$

Có $\dfrac{MT}{MB}=\dfrac{MA}{MT}\Rightarrow M{{T}^{2}}=MA.MB$ (cặp cạnh tương ứng tỉ lệ)

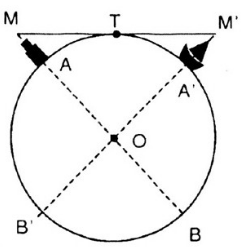
Trên bờ biển có một ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát ở độ cao 10m so với mực nước biển và bán kính Trái Đất gần bằng 6400km (h.30)?

Hướng dẫn: Áp dụng kết quả của bài tập 34.

Phương pháp giải

Sử dụng kết quả của bài tập 34.

- Tính độ dài TM, TM' dưa vào hai công thức $M{{T}^{2}}=MA.MB$ và $MT{{'}^{2}}=M'A'.M'B'$

- Số km để người quan sát tàu bắt đầu thấy ngọn hải đăng là $MM'=MT+TM'$

Hướng dẫn giải

Dựng hình vẽ như hình trên:

Áp dụng kết quả bài 34 ta có: 

$\begin{aligned} & \begin{aligned} M{{T}^{2}}&=MA.MB \\ & =MA\left( MA+AB \right) \\ & =0,04.(0,04+2.6400) \\ & =512,0016 \\ \end{aligned} \\ \Rightarrow &MT\approx 22,63\,\,(km) \\ \end{aligned}$

Tương tự ta tính M’T:

$\begin{aligned} & \begin{aligned} MT{{'}^{2}}&=M'A'.M'B' \\ & =0,01.(0,01+6400.2) \\ & =128,0001 \\ \end{aligned} \\ \Rightarrow& M'T\approx 11,31\left( km \right) \\ \end{aligned}$

Ta có: $MM'=MT+TM'\approx 22,63+11,31=33,94\left( km \right)$

Vậy khi cách ngọn hải đăng 33,94 km thì người quan sát tàu bắt đầu thấy ngọn hải đăng.