Giải bài tập SGK Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau

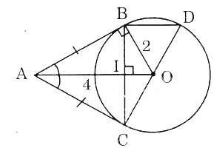
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết \(OB = 2cm, OA = 4cm\).

Phương pháp giải

a) Tính chất hai tiếp tuyến cắt nhau: cho (O;R) với hai tiếp tuyến AB, AC. Khi đó:

+) AB = AC

+) AO là phân giác của góc BAC

b) Sử dụng tính chất: nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác thì tam giác đó là tam giác vuông

c) +) Dùng định nghĩa tỉ số lượng giác trong tam giác vuông: \(\sin \alpha = \dfrac{cạnh\ đối}{cạnh\ huyền}\) để tính số đo góc.

+) Tam giác cân có một góc bằng \(60^o\) thì là tam giác đều.

+) Dùng định lí Pytago: \(\Delta{ABC}\) vuông tại A thì \(BC^2=AC^2+AB^2\)

Hướng dẫn giải

a) Ta có: \(AB = AC\) (tính chất của hai tiếp tuyến cắt nhau)

Suy ra \(ΔABC\) cân tại A.

Lại có \(\widehat{BAO}=\widehat{CAO} \) (tính chất của hai tiếp tuyến cắt nhau)

Suy ra \(AO ⊥ BC\). 

b) Gọi I là giao điểm của AO và BC. 

Suy ra \(BI = IC\) (định lí đường kính và dây cung).

Xét \(ΔCBD\) có :

\(CI = IB\)

\(CO = OD\) (cùng bằng bán kính)

\( \Rightarrow BD // IO\) (IO là đường trung bình của \(\Delta BCD\)) 

\(\Rightarrow BD // AO.\)

c) Áp dụng định lí Pytago trong tam giác vuông OAC:

\(\begin{align} & O{{A}^{2}}=A{{B}^{2}}+O{{B}^{2}} \\ & \Rightarrow AB=\sqrt{O{{A}^{2}}-O{{B}^{2}}}\text{=}\sqrt{{{4}^{2}}-{{2}^{2}}}\text{ =2}\sqrt{3}\text{ }\left( cm \right) \\ \end{align}\)

Trong tam giác vuông OAB có

\(\begin{aligned} & \sin \widehat{OAB}=\dfrac{OB}{OA}=\dfrac{2}{4}=\dfrac{1}{2} \\ & \Rightarrow \widehat{OAB}={{30}^{o}}\Rightarrow \widehat{BAC}=2\widehat{OAB}={{2.30}^{o}}={{60}^{o}} \\ \end{aligned}\)

Tam giác ABC cân tại A có \(\widehat{A}={{60}^{o}}\) nên là tam giác đều.

Do đó \(AB = BC = AC = 2\sqrt3 (cm)\).

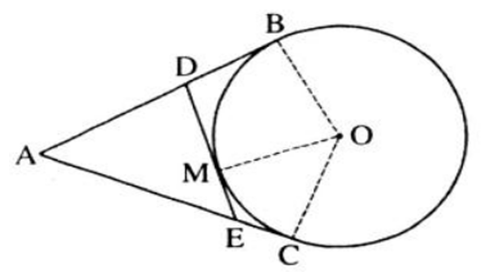
Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Phương pháp giải

+) Sử dụng tính chất hai tiếp tuyến cắt nhau: cho \((O;R)\) với hai tiếp tuyến \(AB,\ AC\) tại \(B,\ C\) của \((O)\) khi đó \(AB=AC\).

+) Chu vi tam giác \(ABC\) là: \(C_{\Delta{ABC}}=AB+BC+AC\). 

Hướng dẫn giải

Theo tính chất hai tiếp tuyến cắt nhau ta có:
 \(DM = DB, EM = EC, AB = AC\)
Chu vi tam giác ADE bằng:
\(\begin{align} AD + DE + AE &= AD + DM + ME + AE \\ &= AD + DB + EC + AE \\ &= AB + AC = 2AB \end{align}\)

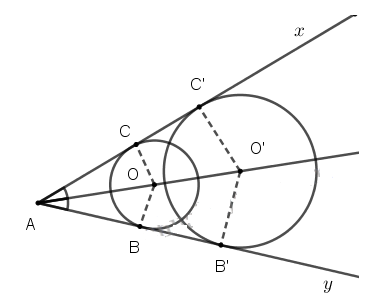
Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?

Phương pháp giải

Vẽ đường tròn tiếp xúc với hai cạnh của góc xAy và dự đoán tâm nằm trên đường đặc biệt nào của góc xAy.

Hướng dẫn giải

Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh của góc xAy. 

Suy ra Ax, Ay là các tiếp tuyến của đường tròn (O).

Suy ra \(\widehat{xAO}=\widehat{yAO}\) (tính chất hai tiếp tuyến cắt nhau)

Hay AO là tia phân giác của góc xAy.

Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.

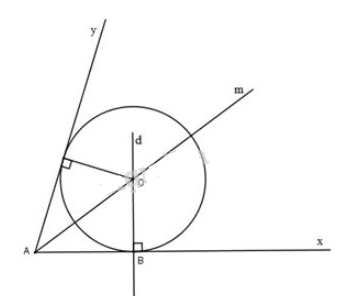
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Phương pháp giải

Bài toán dựng hình chia làm \(4\) bước:

Bước 1. Phân tích: giả sử hình cần dựng đã được vẽ. Lập luận để tìm cách dựng được hình.

Bước 2. Dựng hình: Dựa vào bước phân tích trên liệt kê thứ tự các phép dựng hình cơ bản.

Bước 3. Chứng minh: Bằng lí luận, chứng minh hình vừa dựng thỏa mãn tất cả các giả thiết của bài toán.

Bước 4. Biện luận: thiết lập điều kiện giải được của bài toán. Tức là xét xem bài toán giải được trong trường hợp nào và có bao nhiêu nghiệm. 

Hướng dẫn giải

Phân tích: Giả sử đã dựng được hình thỏa mãn đề bài. Khi đó:

Đường tròn \((O)\) tiếp xúc với hai cạnh của góc \(xAy\) nên tâm \(O\) nằm trên tia phân giác \(Am\) của góc \(xAy\)

Đường tròn \((O)\) tiếp xúc với \(Ax\) tại \(B\) nên tâm \(O\) nằm trên đường thẳng \(d\perp Ax\) tại \(B\). 

Vậy \(O\) là giao điểm của tia \(Am\) với đường thẳng \(d\).

Cách dựng

- Dựng tia phân giác Am của góc \(xAy\).

- Qua \(B\) dựng đường thẳng \(d\perp Ax\), cắt tia \(Am\) tại \(O\).

- Dựng đường tròn \((O;OB)\), đó là đường tròn phải dựng.

Chứng minh

Vì \(OB\perp Ax\) tại \(B\) nên đường tròn \((O;OB)\) tiếp xúc với \(Ax\) tại \(B\). 

Vì \(O\) nằm trên tia phân giác của góc \(xAy\) nên \(O\) cách đều hai cạnh của góc \(xAy\). Do đó đường tròn \((O;OB)\) tiếp xúc với \(Ay\).

Biện luận. Bài toán luôn có một nghiệm hình.