Giải bài tập SGK Toán 9 Bài: Luyện tập
Nội dung giải SGK môn Toán lớp 9 trang 119, 120 được eLib biên soạn và tổng hợp bên dưới đây sẽ giúp các em học sinh học vừa ôn tập kiến thức vừa củng cố kĩ năng làm bài. Thông qua hệ thống 7 bài tập có hướng dẫn giải chi tiết để các em có thể đối chiếu với bài làm của mình từ đó có kế hoạch học tập phù hợp. Mời các em cùng tham khảo.
Mục lục nội dung

1. Giải bài 23 trang 119 SGK Toán 9 tập 2
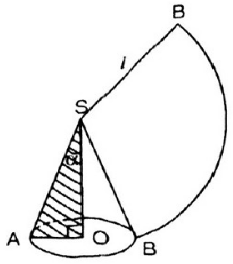
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc α của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).
Phương pháp giải
+) Diện tích hình quạt có số đo n0 của đường tròn bán kính R là: \(S=\dfrac{\pi R^2 n}{360}\)
+) Diện tích xung quanh của hình nón bán kính đáy R và đường sinh l là: \(S_{xq}=\pi Rl.\)
Hướng dẫn giải
Diện tích hình quạt :
\(S_{quạt} = \dfrac{\pi r^2 n^o}{360^o}= \dfrac{\pi.l^2.90}{360}=\dfrac{\pi.l^2}4.\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)
Theo đầu bài ta có: \({S_{xq}} = S_{quạt} \Rightarrow πrl= \dfrac{\pi.l^2}4.\)
Vậy l = 4r.
Suy ra \(\sin \alpha =\dfrac {OA}{SA}= \dfrac{r}l = \dfrac {1}4\) (vì l = 4r)
Vậy \(\alpha= {14^0}28'.\)
2. Giải bài 24 trang 119 SGK Toán 9 tập 2
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là \(120^o\). Tang của nửa góc ở đỉnh của hình nón là:
|
(A) \(\dfrac{\sqrt 2} 4\) |
(B) \(\dfrac{\sqrt 2}{2}\) |
(C) \(\sqrt 2\) |
(D) \(2\sqrt{2}\) |
Hãy chọn kết quả đúng.
Phương pháp giải
+) Ta có: \(h^2=l^2-r^2.\)
+) Gọi góc cần tính là \(\alpha.\) Khi đó: \(\tan \alpha=\dfrac{r}{h}.\)
Hướng dẫn giải
Độ dài cung tròn hình quạt là:
\(l=\dfrac {\pi rn}{180}=\dfrac{\pi.16.120}{180}=\dfrac{32\pi}{3}\,cm\)
Suy ra chu vi đáy hình nón là \(\dfrac {32\pi}{3}\) cm.
Do vậy
\(2\pi r=\dfrac{32\pi}{3}\Rightarrow r=\dfrac{16}{3}\,cm\)
Đường cao hình nón là. \(\sqrt{16^2-\dfrac{16^2}9}=\dfrac {32\sqrt{3}}{2}\,cm\)
Tang góc nửa đường tròn là:
\(\tan\alpha=\dfrac{r}{h}=\dfrac{16}{3}:\dfrac{32\sqrt{3}}{2}=\dfrac{\sqrt{2}}{4}\)
3. Giải bài 25 trang 119 SGK Toán 9 tập 2
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là \(a, b\) (\(a < b\)) và độ dài đường sinh là \(l\) (\(a, b, l\) có cùng đơn vị đo).
Phương pháp giải
Hình nón cụt có r1, r2 là các bán kính đáy, l là độ dài đường sinh có diện tích xung quanh là: Sxq=π(r1+r2)l
Hướng dẫn giải
Theo công thức tính diện tích xung quanh của hình nón cụt, ta có:
\(S_{xq}=\pi(r_1+r_2)l=\pi(a+b)l\)
4. Giải bài 26 trang 119 SGK Toán 9 tập 2
Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):
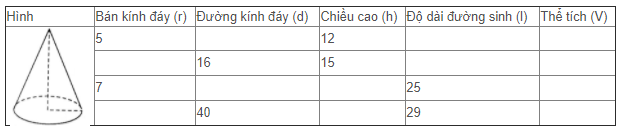
Phương pháp giải
Cho hình nón có chiều cao h, bán kính đáy r và đường sinh l. Khi đó:
+) Đường kính đáy: d = 2r.
+) Thể tích hình nón: \(V=\dfrac{1}{3} \pi r^2h.\)
+) Mối quan hệ \(l^2=h^2+r^2.\)
Hướng dẫn giải
Lấy \(\pi=3,14\)
+ Dòng thứ nhất: Khi r = 5cm; h = 12cm ta có
- Đường kính d = 2r = 2.5 = 10cm
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.5^2}.12 = 100\pi=314 \left( {c{m^3}} \right)\)
+ Dòng thứ hai: Khi d = 16cm; h = 15cm ta có
- Bán kính \(r = \dfrac{d}{2} = \dfrac{{16}}{2} = 8cm\)
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {{15}^2}} = 17\,cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.8^2}.15 = 320\pi =1004,8\left( {c{m^3}} \right)\)
+ Dòng thứ ba: Khi r = 7cm; l = 25cm ta có
- Đường kính d = 2r = 2.7 = 14cm
- Vì \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{25}^2} - {7^2}} = 24cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.7^2}.24 = 392\pi \approx 1230,9\left( {c{m^3}} \right)\)
+ Dòng thứ tư: Khi d = 40cm; l = 29cm ta có
- Đường kính \(r = \dfrac{d}{2} = \dfrac{{40}}{2} = 20cm\)
- Vì \({l^2} = {h^2} + {r^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{20}^2}} = 21cm\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.20^2}.21 = 2800\pi =8792 \left( {c{m^3}} \right)\)
Ta được bảng sau:
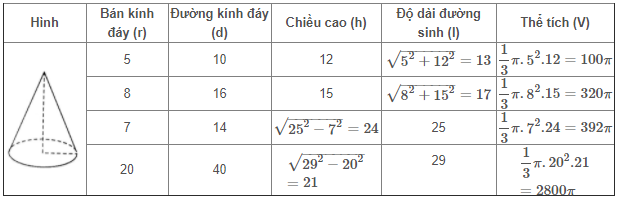
5. Giải bài 27 trang 119 SGK Toán 9 tập 2
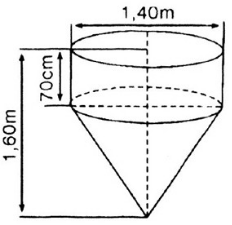
Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 100. Hãy tính:
a) Thể tích của dụng cụ này.
b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).
Phương pháp giải
Công thức tính:
- Hình trụ có chiều cao h và bán kính đáy r có: \(V=\pi r^2.h;\,\,S_{xq}=2\pi r h\)
- Hình nón có chiều cao h và bán kính đáy r là: \(V=\dfrac 1 3 \pi r^2.h;\,\,S_{xq}=\pi rl=\pi r\sqrt{h^2+r^2}\)
- Diện tích xung quanh hình trụ: \(S_{xq \, \, trụ}= 2\pi rh.\)
- Diện tích xung quanh hình nón: \(S_{xq \, \, nón}= \pi rl.\)
Hướng dẫn giải
a) Thể tích của dụng cụ bằng tổng thể tích của một hình trụ có chiều cao là \(70 cm =0,7 m\), bán kính đáy 0,7 m và hình nón có chiều cao 0,9 m và bán kính đáy 0,7 m.
- Thể tích hình trụ là:
\(V_1=\pi r^2h=\pi.0,7^2.0,7\approx 1,08\,m^3\)
- Thể tích hình nón là:
\(V_2=\dfrac 1 3 \pi r^2.h=\dfrac 1 3 .\pi.0,7^2.0,9\approx0,46\,m^3\)
Vậy thể tích của dụng cụ là:
\(V=V_1+V_2\approx 1,08+0,46=1,54\,m^3\)
b) Diện tích mặt ngoài của dụng cụ bằng tổng diện tích xung quanh của một hình trụ có chiều cao là \(70 cm =0,7 m\), bán kính đáy 0,7 m và hình nón có chiều cao 0,9 m và bán kính đáy 0,7 m.
- Diện tích xung quanh hình trụ là:
\(S_1=2\pi rh=2\pi.0,7.0,7\approx3,08\,m^2\)
- Diện tích xung quanh của hình nón là:
\(S_2=\pi rl=\pi.r.\sqrt{h^2+r^2}=\pi.0,7.\sqrt{0,9^2+0,7^2}\approx 2,51\,m^2\)
Diện tích xung quanh của dụng cụ là:
\(S=S_1+S_2\approx 3,08+2,51=5,59\,m^2\)
6. Giải bài 28 trang 120 SGK Toán 9 tập 2
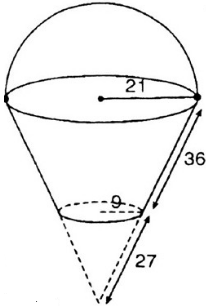
Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm).
a) Hãy tính diện tích xung quanh của xô.
b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu?
Phương pháp giải
+) \(S_{xq \, \, xô}= S_{xq \, \, hình \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn} - S_{xq \, \, hình \, \, nón \, \, nhỏ}.\)
+) \(S_{xq \, \, nón}=\pi rl.\)
+) \(V_{nón}=\dfrac{1}{3}\pi r^2h.\)
Hướng dẫn giải
a) Diện tích xung quanh của xô là:
\(S_{xq}=\pi(r_1+r_2)l=\pi(21+9).36=1080\pi\,cm^2\)
b)Dung tích của xô bằng thể tích của hình nón cụt có đáy nhỏ là 9, đáy lớn là 21 và độ dài đường sinh là 36.
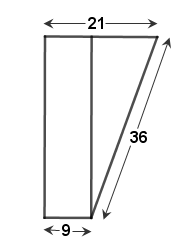
Chiều cao của hình nón cụt là: \(\sqrt{36^2-(21-9)^2}=24\sqrt 2\)
Thể tích hình nón là: \(\dfrac 1 3 \pi h (r_1^2+r_2^2+r_1r_2)=\dfrac 1 3 \pi 24\sqrt 2(9^2+21^2+9.21)\approx25258,31\,cm^3\)
7. Giải bài 29 trang 120 SGK Toán 9 tập 2
Cối xay gió của Đôn-ki-hô-tê (từ tác phẩm của Xéc-van-téc (Cervantès).
Phần trên của cối xay gió có dạng một hình nón (h.102). Chiều cao của hình nón là 42cm và thể tích của nó là 17 600 cm3.
Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đên chữ số thập phân thứ hai).
Phương pháp giải
Thể tích hình nón: \(V=\dfrac{1}{3} \pi r^2 h \Rightarrow r= \sqrt{\dfrac{3V}{\pi h}}.\)
Hướng dẫn giải
Ta có:
\(\dfrac 1 3 \pi r^2 h=17600\\ \Rightarrow \dfrac 1 3 \pi r^2 42=17600\\ \Rightarrow r^2\approx 400\\ \Rightarrow r=20\,cm\)
Bán kính đáy của hình nón là 20 cm
Tham khảo thêm
- doc Giải bài tập SGK Toán 9 Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- doc Giải bài tập SGK Toán 9 Bài 3: Hình cầu. Diện tích hình cầu và thể tích hình cầu
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập