Giải bài tập SGK Toán 9 Bài 6: Cung chứa góc

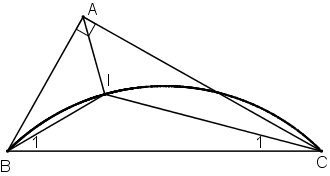
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Phương pháp giải

Xét tam giác IBC

Ta có: \(\widehat{IBC}+\widehat{BIC}+\widehat{BCI}={{180}^{o}}\)

Từ đó ta tính được \(\widehat{BIC} \). 

Chứng minh I luôn nhìn BC dưới một góc không đổi.

Hướng dẫn giải

Xét tam giác ABC vuông tại A ta có:

\(\widehat{BAC}={{90}^{o}} \)

\(\Rightarrow \widehat{B}+\widehat{C}={{90}^{o}} \)

Có IB và IC lần lượt là tia phân giác của góc B và góc C nên 

\(\begin{aligned} & \widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}=\dfrac{1}{2}.\widehat{B}; \\ & \widehat{{{C}_{1}}}=\widehat{{{C}_{2}}}=\dfrac{1}{2}.\widehat{C} \\ & \Rightarrow \widehat{{{B}_{2}}}+\widehat{{{C}_{2}}}=\dfrac{1}{2}\widehat{B}+\dfrac{1}{2}\widehat{C}=\dfrac{1}{2}\left( \widehat{B}+\widehat{C} \right)=\dfrac{1}{2}{{.90}^{o}}={{45}^{o}} \\ \end{aligned}\)

Trong tam giác IBC có:

\(\begin{aligned} & \widehat{IBC}+\widehat{BIC}+\widehat{BCI}={{180}^{o}} \\ & \Leftrightarrow \widehat{{{B}_{2}}}+\widehat{{{C}_{2}}}+\widehat{BIC}={{180}^{o}} \\ & \Leftrightarrow {{45}^{o}}+\widehat{BIC}={{180}^{o}} \\ & \Leftrightarrow \widehat{BIC}={{135}^{o}} \\ \end{aligned} \)

Như vậy, điểm I nhìn đoạn BC cố định góc \(135^o\) không đổi.

Vậy quỹ tích của I là cung chứa góc \(135^o\) dựng trên đoạn thẳng BC.

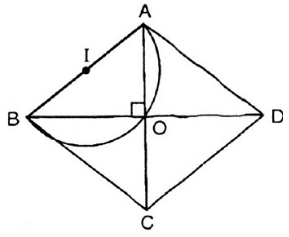
Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo của các hình thoi đó.

Phương pháp giải

- Thông thường, bài toán quỹ tích ta làm theo các bước:

Bước 1: Dự đoán quỹ tích

Bước 2: Chứng minh quỹ tích: gồm Phần thuận và Phần đảo

Bước 3: Kết luận.

- Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

Hướng dẫn giải

Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.

Chứng minh: 

Phần thuận:

Ta đã biết rằng hai đường chéo hình thoi vuông góc với nhau hay \(AC \bot BD\) tại O.

Vậy điểm O nhìn AB cố định dưới góc \(90^0.\)

Suy ra: Quỹ tích điểm O là nửa đường tròn đường kính AB.

Phần đảo: 

Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.

+ Lấy điểm O thuộc nửa đường tròn đường kính AB

+ Lấy C đối xứng với A qua O

+ Lấy D đối xứng với B qua O.

Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường

⇒ ABCD là hình bình hành.

Mà O thuộc nửa đường tròn đường kính AB 

\(⇒ \widehat {AOB} = {90^0}\)

⇒ AC ⊥ DB

⇒ Hình bình hành ABCD là hình thoi.

Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)

Dựng một cung chứa góc \(55^o\) trên đoạn thẳng \(AB = 3cm.\)

Phương pháp giải

Cách vẽ cung chứa góc \( \alpha\) dựng trên đoạn AB

+ Vẽ tia Ax tạo với AB một góc \(\alpha\)

+ Vẽ đường thẳng \(Ay \bot Ax\)

+ Vẽ đường trung trực d của đoạn thẳng AB. Gọi O là giao của Ay với d.

+ Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.

Cung AmB là một cung chứa góc \(\alpha\)

Hướng dẫn giải

Dựng hình:

- Kẻ đoạn thẳng \(AB=3 cm\).

- Dựng góc \(BAx=55^o\).

- Qua A kẻ đường thẳng Ay vuông góc với Ax.

- Dựng đường thẳng d là trung trực của AB.

- Ay và d cắt nhau tại O.

- Dựng đường tròn tâm O bán kính OA. 

Cung lớn AB là cung cần dựng.

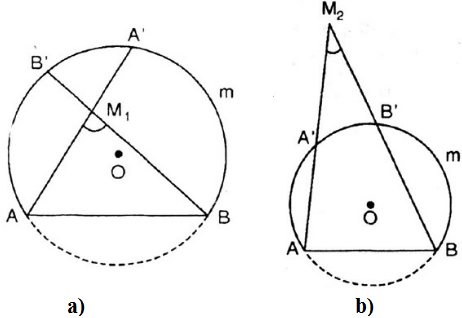
Gọi cung chứa góc \(55^o\) ở bài tập 46 là cung \(AmB\). Lấy điểm \(M_1\) nằm bên trong và điểm \(M_2\) nằm bên ngoài đường tròn chứa cung này sao cho \(M_1, M_2\) và cung \(AmB\) nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:

a) \(\widehat{AM_1B}>55^o\)

b) \(\widehat{AM_2B}<55^o\)

Phương pháp giải

a) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn

Nên ta có: \(\widehat{A{{M}_{1}}B}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{A'B'}+\text{sđ}\overset\frown{AB} \right)\)

b) Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

Nên ta có: \(\widehat{A{{M}_{2}}B}=\dfrac{1}{2}\left( \text{sđ}\overset\frown{AB}\text{-sđ}\overset\frown{A'B'} \right)\)

Hướng dẫn giải