Giải bài tập SGK Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn

Vẽ một tam giác vuông có một góc nhọn $34^{\circ}$ rồi viết các tỉ số lượng giác của góc $34^{\circ}$.

Phương pháp giải

- Vẽ tam giác thỏa mãn yêu cầu đề bài. 

- Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:

$\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};$         $\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}$;

$\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};$             $\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.$

Hướng dẫn giải

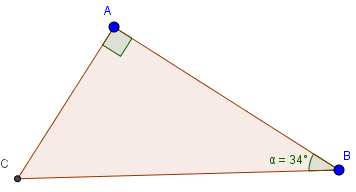
Vẽ tam giác $ABC$ vuông tại $A$ với $\widehat{B}=34^{\circ}$.

Để vẽ được tam giác đề yêu cầu, chúng ta thực hiện các bước như sau:

B1. Vẽ đoạn thẳng $AB$ với độ dài bất kì.

B2. Từ $A$ dựng tia $Ax$ vuông góc với đoạn thẳng $AB$

B3. Từ $B$ dùng thước đo góc vẽ tia $By$ sao cho góc $ABy$ bằng $34$ độ.

B4. $Ax$ và $By$ cắt nhau tại $C$. 

B5. Nối các điểm lại với nhau ta được tam giác $ABC$ cần dựng.

Tỉ số lượng giác của góc $\widehat{B}=34^o$ là

$\sin 34^o=\sin B=\dfrac{AC}{BC}$

$\cos 34^o=\cos B=\dfrac{AB}{BC}$

$\tan 34^o=\tan B=\dfrac{AC}{AB}$

$\cot 34^o=\tan C=\dfrac{AB}{AC}$

Cho tam giác ABC vuông tại C, trong đó $AC= 0,9 m$, $BC=1,2 m$. Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A

Phương pháp giải

- Dùng định lí Pytago để tính độ dài cạnh huyền.

- Dựa vào định nghĩa tỉ số lượng giác để tính các tỉ số lượng giác của góc $B$.

$\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};$         $\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}$;

$\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};$             $\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.$

- Dựa vào định lí về tỉ số lượng giác của hai góc phụ nhau: " Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tan góc này bằng cotang góc kia" để từ các tỉ số lượng giác của góc $B$ tính tỉ số lượng giác của góc $A$.

Hướng dẫn giải

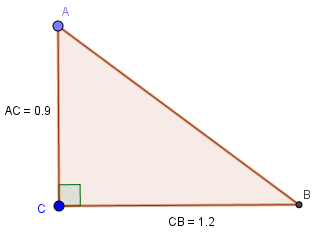
Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

$AB=\sqrt{AC^2+BC^2}=\sqrt{0,9^2+1,2^2}=1,5$

Từ đó, ta có

$sinA=cosB=\frac{BC}{AB}=\frac{4}{5}$

$sinB=cosA=\frac{AC}{AB}=\frac{3}{5}$

$tanA=cotB=\frac{BC}{AC}=\frac{4}{3}$

$tanB=cotA=\frac{AC}{BC}=\frac{3}{4}$

Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 450: $sin 60^{\circ},cos75^{\circ}, sin52^{\circ}30', cotg82^{\circ}, tg80^{\circ}$

Phương pháp giải

Nếu $\alpha$ và $\beta$ là hai góc phụ nhau (tức $\alpha + \beta=90^o \Rightarrow \alpha = 90^o - \beta)$ thì ta có

$\sin \alpha =\cos (90^o -\alpha)= \cos \beta$;           

$\sin \beta = \cos (90^o- \beta)=\cos \alpha$;         

$\tan \alpha =\cot (90^o - \beta)=\cot \beta$;

$\tan \beta = \cot (90^o - \alpha)=\cot \alpha$.

Hướng dẫn giải

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có

$\sin 60^o=\cos (90^o-60^o)=\cos 30^o$

$\cos 75^o=\sin (90^o-75^o)=\sin 15^o$

$\sin 52^o30'=\cos (90^o-52^o 30')=\cos 37^o 30'$

$\cot 82^o=\tan (90^o - 82^o)=\tan 8^o$

$\tan 80^o=\cot (90^o - 80^o)=\cot 10^o$.

Dựng góc nhọn $\alpha$, biết

a) $sin\alpha =\frac{2}{3}$

b) $cos\alpha =0,6$

c) $\tan \alpha  = \frac{3}{4}$

d) $cotg\alpha  = \frac{3}{2}$

Phương pháp giải

• Dựng một tam giác vuông có hai cạnh là $m$ và $n$ (trong đó $m,\ n$ là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)
• Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc $\alpha$.

Hướng dẫn giải

Câu a

$sin\alpha =\frac{2}{3}$

Chúng ta tính cạnh còn lại bằng định lí Pytago:

$=\sqrt{3^2-2^2}=\sqrt{5}$

Vậy ta sẽ vẽ một góc vuông, và vẽ hai độ lớn là $2$ và $\sqrt{5}$

Hình trên cho ta thấy

$sin\alpha =sinACB=\frac{2}{3}$

Câu b

$cos\alpha =0,6=\frac{3}{5}$

Tương tự câu a, ta sẽ tính độ lớn cạnh góc vuông còn lại bằng Pytago:

$=\sqrt{5^2-3^2}=4$

Vậy ta sẽ vẽ một góc vuông, và vẽ hai độ lớn là $3$ và $4$

Hình trên cho ta thấy:

$cos\alpha =cosABC=\frac{3}{5}=0,6$

Câu c

Đối với bài này, ta sẽ vẽ tam giác vuông có hai cạnh có độ lớn là $3$ và $4$

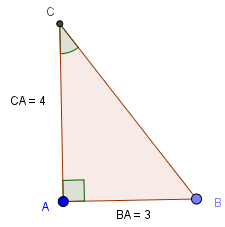
Hình trên cho ta thấy

$tan\alpha =tanACB=\frac{3}{4}$

Câu d: Cũng tương tự với câu c:

$cotg \alpha  = \frac{3}{2}$

Đối với bài này, ta sẽ vẽ tam giác vuông có hai cạnh có độ lớn là $3$ và $2$

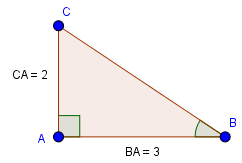
Hình trên cho ta thấy

$cot\alpha =cotABC=\frac{3}{2}$

Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn  tùy ý, ta có:

a) $tg\alpha =\frac{sin\alpha }{cos\alpha}$

$cotg\alpha =\frac{cos\alpha }{sin\alpha }$

$tg\alpha.cotg\alpha =1$

b) $sin{\alpha ^2} + \cos{\alpha ^2} = 1$

Gợi ý: Sử dụng định lý Py-ta-go

Phương pháp giải

- Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:

$\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};$         $\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}$;

$\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};$             $\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.$

- Sử dụng định lí Pytago trong tam giác vuông: $\Delta{ABC}$ vuông tại $A$, khi đó: $BC^2=AB^2+AC^2$ 

Hướng dẫn giải

Ta sẽ sử dụng hình trên để chứng minh các câu trên.

 $\widehat{\alpha}=\widehat{ABC}$

Câu a: Ta có

$\frac{sin\alpha}{cos\alpha}=\frac{AC}{BC}:\frac{AB}{BC}=\frac{AC}{BC}.\frac{BC}{AB}=\frac{AC}{AB}$

$=tanABC=tan\alpha$

Tương tự, ta có

$\frac{cos\alpha}{sin\alpha}=\frac{AB}{BC}:\frac{AC}{BC}=\frac{AB}{BC}.\frac{BC}{AC}=\frac{AB}{AC}$

$=cotABC=cot\alpha$

Theo hai ý trên, ta có:

$tan\alpha.cot\alpha=\frac{sin\alpha}{cos\alpha}.\frac{cos\alpha}{sin\alpha}=1$

Câu b

$sin ^{2}\alpha +cos^{2}\alpha =\frac{AC^{2}}{BC^{2}}+\frac{AB^{2}}{BC^{2}}=\frac{BC^{2}}{BC^{2}}=1$

Nhận xét đối với cách hệ thức trên

$tan\alpha =\frac{sin\alpha }{cos\alpha }$

$cotg\alpha =\frac{cos\alpha }{sin\alpha }$

$tg\alpha.cotg\alpha =1$

$sin^{2}\alpha +cos^{2}\alpha =1$

là những hệ thức cơ bản cần nhớ để giải một số bài tập khác

Cho tam giác ABC vuông tại A. Biết $cosB=0,8$; hãy tính các tỷ số lượng giác của góc C.

Gợi ý: sử dụng bài tập 14

Phương pháp giải

• Nếu $\widehat B$ và $\widehat C$ là hai góc phụ nhau, biết $\cos B$, sử dụng công thức: $\sin C =\cos B$. Ta tính được $\sin C$. 
• Biết $\sin \alpha$, dùng công thức $\sin^2 \alpha+\cos^2 \alpha =1$ tính được $\cos \alpha$.
• Dùng công thức  $\tan \alpha =\dfrac{\sin\alpha }{\cos \alpha}$, biết $\sin \alpha$ và $\cos \alpha$ tính được $\tan \alpha$.
• Dùng công thức:$\tan \alpha . \cot \alpha =1$, biết $\tan \alpha$ tính được $\cot \alpha$.

Hướng dẫn giải

Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế

$sinC>0;cosC>0;tanC>0;cotC>0$

Ta có

$\widehat{ABC}+\widehat{ACB}=90^o$

$\Rightarrow sinC=cosB=0,8$

Lại có

$sin^2C+cos^2C=1\Rightarrow cos^2C=1-sin^2C=1-0,8^2=0,36$

$\Rightarrow cosC=0,6(cosC>0)$

$\Rightarrow tanC=\frac{sinC}{cosC}=\frac{0,8}{0,6}=\frac{4}{3}$

$\Rightarrow cotC=\frac{cosC}{sinC}=\frac{0,6}{0,8}=\frac{3}{4}$

Cho tam giác vuông có một góc bằng $60^{\circ}$ và cạnh huyền có độ dài bằng $8$. Hãy tìm độ dài của cạnh đối diện góc $60^{\circ}$.

Phương pháp giải

Dựa vào định nghĩa tỷ số lượng giác của góc nhọn:

$\sin \alpha =\dfrac{cạnh\ đối}{cạnh \ huyền}$

$\Rightarrow {cạnh\ đối} = \sin \alpha. {cạnh\ huyền}.$

Hướng dẫn giải

Xét $\Delta{ABC}$ vuông tại $A$ có $\widehat B=60^0$, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

$\sin B = \dfrac{AC}{BC} \Leftrightarrow \sin 60^o = \dfrac{AC}{8}$

$\Leftrightarrow AC =8. \sin 60^o=8.\dfrac{\sqrt 3}{2}=4\sqrt 3.$

Vậy cạnh đối diện với góc $60^o$  là $AC=4\sqrt 3$.

Tìm giá trị của x trong hình 23

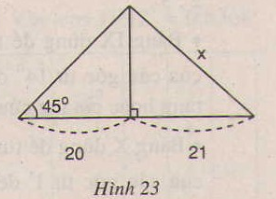
Phương pháp giải

• Sử dụng tỷ số lượng giác: $\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề} \Rightarrow {cạnh\ đối}=\tan \alpha . {cạnh\ kề}$. 
• Dùng định lí Pytago trong tam giác vuông biết hai cạnh góc vuông, tính được cạnh huyền.

Hướng dẫn giải

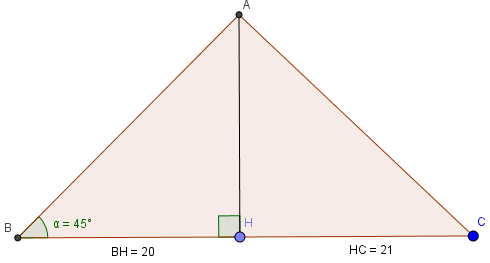
Vậy độ dài AC chính là x cần tìm.

Xét tam giác BHA vuông tại H có

$\left\{\begin{matrix} \widehat{ABC}=45^o\\ BH\perp HA \end{matrix}\right.$

Vậy tam giác ABH vuông cân tại H.

$\Rightarrow BH=AH=20$

Áp dụng định lí Pytago vào tam giác AHC vuông tại H ta có:

$AC=\sqrt{AH^2+HC^2}=\sqrt{20^2+21^2}=29$

Vậy $x=29$