Giải bài tập SGK Toán 9 Bài: Luyện tập

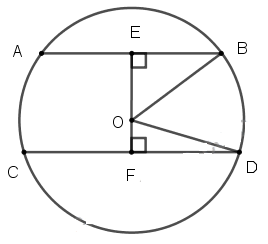
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.

Phương pháp giải

- Bước 1: Kẻ $OE ⊥ AB, OF ⊥ CD$. Tính EA, EF.

- Bước 2: Tính OE, OF.

- Bước 3: Áp dụng định lí Pitago trong tam giác vuông OFD, tính FD. Từ đó tính CD

Hướng dẫn giải

Kẻ $OE ⊥ AB, OF ⊥ CD$.

$\Rightarrow EA=EB=\dfrac{AB}{2}=20\,\left( cm \right)$ (định lí đường kính và dây cung)

Ta thấy $E, O, F$ thẳng hàng nên EF là khoảng cách giữa hai dây AB và CD $\Rightarrow EF=22cm$. 

Áp dụng định lí Pitago trong tam giác vuông OEB có:

$\begin{aligned} & O{{B}^{2}}=O{{E}^{2}}+E{{B}^{2}} \\ & \Rightarrow OE=\sqrt{O{{B}^{2}}-E{{B}^{2}}}=\sqrt{{{25}^{2}}-{{20}^{2}}}=15\,\left( cm \right) \\ \end{aligned}$

$\Rightarrow OF=EF-OE=22-15=7\,\left( cm \right)$

Áp dụng định lí Pitago trong tam giác vuông OFD có:

$\begin{aligned} & O{{D}^{2}}=O{{F}^{2}}+F{{D}^{2}} \\ & \Rightarrow FD=\sqrt{O{{D}^{2}}-O{{F}^{2}}}=\sqrt{{{25}^{2}}-{{7}^{2}}}=24\,\left( cm \right) \\ \end{aligned}$

$\Rightarrow CD=2FD=2.24=48\,\left( cm \right)$ (định lí đường kính và dây cung)

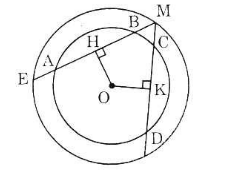
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết $AB > CD$.

Hãy so sánh các độ dài:

a) OH và OK

b) ME và MF

c) MH và MK

Phương pháp giải

- Để so sánh hai dây, ta đi so sánh khoảng cách từ tâm đến hai dây ấy và ngược lại.

- Sử dụng tính chất: Trong một đường tròn:

a) Dây nào lớn hơn thì dây đó gần tâm hơn.

b) Dây nào gần tâm hơn thì dây đó lớn hơn.

c) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Hướng dẫn giải

a) Xét trong đường tròn nhỏ:

Trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Theo giả thiết AB > CD suy ra AB gần tâm hơn, tức là  OH < OK

b) Xét trong đường tròn lớn:

Trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Theo câu a, ta có: $OH < OK \Rightarrow ME > MF$

c) Xét trong đường tròn lớn:

Vì  $OH \bot ME \Rightarrow EH=MH=\dfrac{ME}{2}$

Vì $OK \bot MF \Rightarrow KF=MK=\dfrac{MF}{2}$

Theo câu b, ta có: $ME > MF \Rightarrow \dfrac{ME}{2} > \dfrac{MF}{2} \Leftrightarrow MH > MK$

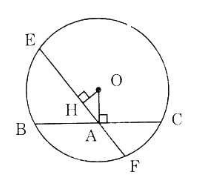
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.

Phương pháp giải

Kẻ $OH ⊥ EF$.

Xét: Dây nào gần tâm hơn thì dây đó lớn hơn.

Hướng dẫn giải

Kẻ $OH ⊥ EF$.

Trong tam giác vuông OHA vuông tại H có $OA > OH$ (đường vuông góc ngắn hơn đường xiên).

Vì $OA > OH$ nên $BC < EF$