Giải bài tập SGK Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số

a) Cho hàm số \(y = f(x) = \dfrac{2}{3} x\)

Tính: \(f(-2);\)  \(f(-1);\)  \( f(0); \)  \(f(\frac{1}{2});\)  \( f(1);\)  \( f(2); \) \(f(3)\)

b) Cho hàm số \(y = g(x) = \dfrac{2}{3} x + 3\).

Tính: \(g(-2);\)  \( g(-1);\)  \( g(0);\)  \( g(\dfrac{1}{2});\)  \( g(1);\)  \( g(2);\)  \( g(3)\)

c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến \(x\) lấy cùng một giá trị ?

Phương pháp giải

+) Giá trị của hàm số \(f(x)\) tại \(x=a\) là \(f(a)\). 

Tức là thay \(x=a\) vào biểu thức của hàm số \(f(x)\) ta tính được \(f(a)\).

+) Giá trị của hàm số \(y=ax+b\) lớn hơn giá trị của hàm số \(y=ax\) là \(b\) đơn vị khi \(x\) lấy cùng một giá trị.

Hướng dẫn giải

Câu a

\(f(-2) = \frac{2}{3}.(-2)=\frac{-4}{3}\)

\(f(-1) = \frac{2}{3}.(-1)=\frac{-2}{3}\)

\(f(0) = \frac{2}{3}.(0)=0\)

\(f(\frac{1}{2}) = \frac{2}{3}.\left ( \frac{1}{2} \right )=\frac{1}{3}\)

\(f(1) = \frac{2}{3}.(1)=\frac{2}{3}\)

\(f(2) = \frac{2}{3}.(2)=\frac{4}{3}\)

\(f(3) = \frac{2}{3}.(3)=2\)

Câu b

\(g(-2) = \frac{2}{3}.(-2)+3=\frac{5}{3}\)

\(g(-1) = \frac{2}{3}.(-1)+3=\frac{7}{3}\)

\(g(0) = \frac{2}{3}.(0)+3=0\)

\(g\left ( \frac{1}{2} \right ) = \frac{2}{3}.\left ( \frac{1}{2} \right )+3=\frac{10}{3}\)

\(g(1) = \frac{2}{3}.(1)+3=\frac{11}{3}\)

\(g(2) = \frac{2}{3}.(2)+3=\frac{13}{3}\)

\(g(3) = \frac{2}{3}.(3)+3=5\)

Câu c

Khi x lấy cùng một giá trị thì giá trị của g(x) lớn hơn giá trị của f(x) là 3 đơn vị.

Cho hàm số \(y = - \frac{1}{2}x + 3\)

a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?

Phương pháp giải

a) Lần lượt thay từng giá trị của \(x\) vào công thức hàm số \(y=f(x)\) ta tính được giá trị \(y\) của hàm số tại điểm đó. 

b) Với \({x_1},{x_2} \in \mathbb{R}\):

Nếu \( x_1  < x_2\)  và   \(f(x_1) < f(x_2)\)  thì hàm số \(y=f(x)\) đồng biến trên \(\mathbb{R}\).

Nếu \( x_1  < x_2\)  và   \(f(x_1) > f(x_2)\)  thì hàm số \(y=f(x)\) nghịch biến trên \(\mathbb{R}\).

Hướng dẫn giải

Câu a

Câu b

Hàm số trên nghịch biến vì khi x tăng lên thì y giảm.

Nhận xét: Hệ số trước x âm thì hàm số nghịch biến trên R, hệ số trước x dương thì hàm số đồng biến trên R

Cho hai hàm số y = 2x và y = -2x

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho

b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?

Phương pháp giải

a) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\):  Cho \(x=x_0 \Rightarrow y_0=ax_0\)

Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)

b) Với \({x_1},{x_2} \in \mathbb{R}\):  

Nếu \( x_1  < x_2\)  và   \(f(x_1) < f(x_2)\)  thì hàm số \(y=f(x)\) đồng biến trên \(\mathbb{R}\).

Nếu \( x_1  < x_2\)  và   \(f(x_1) > f(x_2)\)  thì hàm số \(y=f(x)\) nghịch biến trên \(\mathbb{R}\).

Hướng dẫn giải

Câu a

Đồ thị của hàm số \(y = 2x\) là đường thẳng đi qua \(O(0;0)\) và điểm \(A(1; 2)\)

Đồ thị của hàm số \(y = -2x\) là đường thẳng đi qua \(O(0;0)\) và điểm \(B(1; -2)\)

Câu b

Hàm số \(y = 2x\) đồng biến vì khi x tăng lên thì y tương ứng tăng lên

Hàm số \(y = -2x\) nghịch biến vì khi x tăng lên thì y tương ứng giảm đi

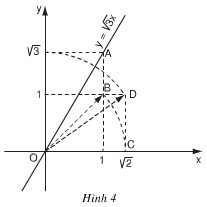
Đồ thị hàm số \(y = \sqrt{3} x\) được vẽ bằng compa và thước thẳng ở hình 4

Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó

Phương pháp giải

+) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\):  Cho \(x=x_0 \Rightarrow y_0=ax_0\)

Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)

+) Sử dụng định lí Py-ta-go: Tam giác \(\Delta ABC\) vuông tại \(A\) thì \(AB^2+ AC^2 =BC^2\). 

Hướng dẫn giải

Ta biết rằng đồ thị hàm số \(y = x\sqrt{3}\)  là một đường thẳng đi qua gốc tọa độ. Hơn nữa, khi \(x = 1\) thì \(y = \sqrt{3}\). Do đó điểm \(A(1; \sqrt{3})\) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải xác định điểm trên  trục tung biểu diễn số \(\sqrt{3}\). Ta có:

\(\sqrt{3}=\sqrt{1+2}=\sqrt{1^2+(\sqrt{2})^2}\)

Hình vẽ trong SGK thể hiện:

 \(OC = OB =\sqrt{ 2}\)

\(OD=\sqrt{OC^2+CD^2}=\sqrt{2+1}=\sqrt{3}\)

Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A

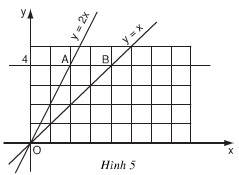
a) Vẽ đồ thị hàm số \(y = x\) và \(y = 2x\) trên cùng một mặt phẳng tọa độ Oxy (h.5)

b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ \(y = 4\) lần lượt cắt các đường thẳng \(y = 2x\), \(y = x\) tại hai điểm A và B

Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimét

Hướng dẫn giải

Câu a

Câu b

\(A(2; 4), B(4; 4)\)

Ta có:

\(AB = 4 - 2 = 2 (cm)\)

Áp dụng định lý Pytago, ta có:

\(OA=\sqrt{2^2+4^2}=2\sqrt{5}(cm)\)

\(OB=\sqrt{4^2+4^2}=4\sqrt{2}(cm)\)

Chu vi tam giác OAB là:

\(P=OA+OB+AB=2+2\sqrt{5}+4\sqrt{2}(cm)\)

Gọi C là điểm biểu diễn số 4 trên trục tung, ta có diện tích tam giác AOB là:

\(S=\frac{1}{2}OC.AB=\frac{1}{2}.4.2=4(cm^2)\)

Cho các hàm số \(y = 0,5x\) và \(y = 0,5x + 2\)

a) Tính giá trị y tương ứng với mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:

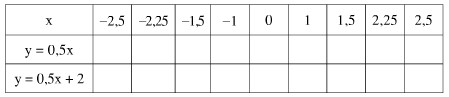
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị?

Phương pháp giải

a) Lần lượt thay từng giá trị của \(x\) vào biểu thức của \(y\) để tính giá trị của hàm số tại điểm đó.

b) Giá trị của hàm số \(y=ax+b\) lớn hơn giá trị của hàm số \(y=ax\) là \(b\) đơn vị khi \(x\) lấy cùng một giá trị.

Hướng dẫn giải

Câu a

Câu b

Khi x lấy cùng một giá trị thì giá trị của hàm số y = 0,5x + 2 lớn hơn giá trị của hàm số y = 0,5x là 2 đơn vị

Cho hàm số \(y = f(x) = 3x\). 

Cho \(x\) hai giá trị bất kì \( x_{1},\ x_{2} \) sao cho \(x_{1}  < x_{2} \) .

Hãy chứng minh \(f(x_{1} ) < f(x_{2} )\) rồi rút ra kết luận hàm số đã cho đồng biến trên \(\mathbb{R}\).

Phương pháp giải

+) Định nghĩa hàm số đồng biến:   Với \({x_1},{x_2} \in \mathbb{R}\):

     Nếu \( x_1  < x_2\)  và   \(f(x_1) < f(x_2)\)  thì hàm số \(y=f(x)\) đồng biến trên \(\mathbb{R}\).

+) Tính chất của bất đẳng thức: Với \(c > 0\) thì: \(a < b \Leftrightarrow a.c < b.c\)

Hướng dẫn giải

Ta có:  

\(f\left( {{x_1}} \right) = 3{x_1}\)

\(f\left( {{x_2}} \right) = 3{x_2}\)

Theo giả thiết, ta có:

\(x_{1} < x_{2} \Leftrightarrow 3.x_{1} < 3.x_{2}\) ( vì \( 3 > 0 \) nên chiều bất đẳng thức không đổi)

\( \Leftrightarrow f(x_1) < f(x_2)\) (vì \(f\left( {{x_1}} \right) = 3{x_1};\)\(f\left( {{x_2}} \right) = 3{x_2})\)

Vậy với \(x_{1} < x_{2}\) ta được \(f(x_1) < f(x_2)\) nên hàm số \(y = 3x\) đồng biến trên \(\mathbb{R}\). 

Chú ý

Ta cũng có thể làm như sau:

Vì \(x_{1}  < x_{2} \) nên \(x_{1}  - x_{2}<0\)

Từ đó: \(f(x_1)-f(x_2)=3x_1-3x_2=3(x_1-x_2)<0\) 

Hay \(f(x_1)

Vậy với \(x_{1} < x_{2}\) ta được \(f(x_1) < f(x_2)\) nên hàm số \(y = 3x\) đồng biến trên \(\mathbb{R}\).