Giải bài tập SGK Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

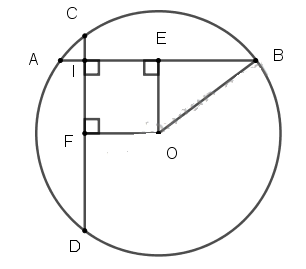
Cho đường tròn tâm O bán kính \(5cm\), dây AB bằng \(8cm\).

a) Tính khoảng cách từ tâm O đến dây AB.

b) Gọi \(I\) là điểm thuộc dây AB sao cho \(AI = 1cm\). Kẻ dây CD đi qua \(I\) và vuông góc với AB. Chứng minh rằng \(CD = AB\).

Phương pháp giải

a) Kẻ OE vuông góc với AB tại E.

Áp dụng định lí Pitago trong tam giác vuông OBE suy ra  khoảng cách từ tâm O đến dây AB

b) Kẻ OF vuông góc với CD tại F.

Xét tứ giác OEIF chứng minh CD = AB (hai dây cách đều tâm thì bằng nhau).

Hướng dẫn giải

a) Kẻ OE vuông góc với AB tại E.

\(\Rightarrow AE=EB=\dfrac{AB}{2}=4\,\left( cm \right)\) (định lí đường kính và dây cung)

Áp dụng định lí Pitago trong tam giác vuông OBE có:

\(\begin{aligned} & O{{B}^{2}}=O{{E}^{2}}+E{{B}^{2}} \\ & \Rightarrow OE=\sqrt{O{{B}^{2}}-E{{B}^{2}}}=\sqrt{{{5}^{2}}-{{4}^{2}}}=3\,\left( cm \right) \\ \end{aligned}\)

Vậy khoảng cách từ tâm O đến dây AB là \(OE= 3cm\).

b) Kẻ OF vuông góc với CD tại F.

Tứ giác OEIF có: \(\widehat{E}=\widehat{I}=\widehat{F}={{90}^{o}}\) nên là hình chữ nhật

Ta có \(IE = AE - AI = 4 - 1 = 3cm \)

\(\Rightarrow OF = IE = 3cm\) (tính chất hình chữ nhật)   

Mà \(OE =3cm\) (chứng minh trên)

Suy ra \(OE=OF \Rightarrow CD = AB\) (hai dây cách đều tâm thì bằng nhau).

Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:

a) \(EH = EK\)

b) \(EA = EC\).

Phương pháp giải

a) 

Bước 1: Nối OE

Bước 2: Xét hai tam giác vuông OEH và OEK chứng minh OH = OK

Bước: Chứng minh: ΔOEH = ΔOEK

b) Chứng minh: EA = EH - HA = EK - KC = EC

Hướng dẫn giải

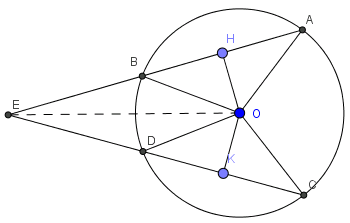
a) Nối OE ta có: 

\(AB = CD \Rightarrow OH = OK\) (định lí 1)

 Vì H, K lần lượt là trung điểm của AB và CD

 Nên \(OH\bot AB,OK\bot CD\) (định lí đường kính và dây cung)

Xét hai tam giác vuông OEH và OEK có: 

OE là cạnh chung 

 \(OH = OK\)

 \(\Rightarrow ΔOEH = ΔOEK\) (cạnh huyền, cạnh góc vuông) 

\(\Rightarrow EH = EK \) (hai cạnh tương ứng)       (1).  

b) Ta có: \(AH=HB, CK=KD\) (tính chất trung điểm) 

Mà \(AB = CD\) (giả thiết) 

Suy ra \(AH = KC \)    (2)

Từ (1) và (2) suy ra: 

\(EA = EH - HA = EK - KC = EC\)

Vậy \(EA = EC\).