Giải bài tập SGK Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung

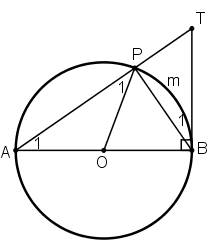
Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh: \(\widehat{APO}=\widehat{PBT}\)

Phương pháp giải

Sử dụng hệ quả: "Trong một đường tròn, góc nội tiếp và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau"

Xét tam giác OPA

Chứng minh \(\widehat{PBT}=\widehat{OAP}\) từ đó suy ra \(\widehat{APO}=\widehat{PBT} \)

Hướng dẫn giải

Xét tam giác OPA có \(OP=OA\) nên OPA cân tại O

\(\Rightarrow \widehat{OPA}=\widehat{OAP} \)

Mà \(\widehat{OAP}\)  là góc nội tiếp chắn cung \(\overset\frown{PmB}\)  và \( \widehat{PBT}\)  là góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(\overset\frown{PmB}\)

Nên \(\widehat{PBT}=\widehat{OAP}\)

Do đó, \(\widehat{APO}=\widehat{PBT} \)

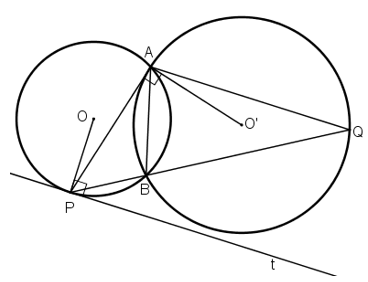
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).

Phương pháp giải

Ta cần chứng minh \( \widehat{AQB}=\widehat{BPx}\)

Xét đường tròn (O’) chứng minh  \(\widehat{PAB}=\widehat{AQB} (1)\)

Xét đường tròn (O) chứng minh \(\widehat{PAB}=\widehat{BPx} (2)\)

Từ (1) và (2) có: \( \widehat{AQB}=\widehat{BPx}\)  

Hướng dẫn giải

Xét đường tròn (O’) có:

\(\widehat{BAP}\)  là góc tạo bởi tia tiếp tuyến và dây cung AP chắn cung \(\overset\frown{AmB} \)

\(\widehat{AQB}\)  là góc nội tiếp chắn cung \(\overset\frown{AmB}\)

Suy ra \(\widehat{PAB}=\widehat{AQB} (1)\)

Xét đường tròn (O) có:

\(\widehat{BPx}\)  là góc tạo bởi tia tiếp tuyến và dây cung PB chắn cung \(\overset\frown{PB}\)

\(\widehat{PAB}\)  là góc nội tiếp chắn cung \(\overset\frown{PB}\)

Suy ra 

\(\widehat{PAB}=\widehat{BPx} (2)\)

Từ (1) và (2) có: \( \widehat{AQB}=\widehat{BPx}\)  

Suy ra \(AQ//Px\) (cặp góc so le trong bằng nhau)

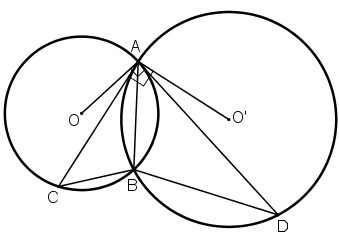
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.

Chứng minh \(\widehat{CBA}=\widehat{DBA}\)

Phương pháp giải

- Chứng minh: 

\(\widehat{ACB}=\widehat{BAD}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB)

 \(\widehat{ADB}=\widehat{BAC}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB)

- Xét \(\Delta ABC\)  và \(\Delta DBA\)  chứng minh \(\widehat{ABC}=\widehat{ABD}\)

Hướng dẫn giải

Xét đường tròn (O) có: 

\(\widehat{ACB}=\widehat{BAD}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB)

Xét đường tròn (O’) có:

\(\widehat{ADB}=\widehat{BAC}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB)

Xét \(\Delta ABC\)  và \(\Delta DBA\)  có:

\(\begin{aligned} & \left\{ \begin{aligned} & \widehat{ACB}=\widehat{BAD} \\ & \widehat{CAB}=\widehat{ADB} \\ \end{aligned} \right. \\ & \Leftrightarrow \widehat{ACB}+\widehat{CAB}=\widehat{BAD}+\widehat{ADB} \\ & \Rightarrow {{180}^{o}}-\left( \widehat{ACB}+\widehat{CAB} \right)={{180}^{o}}-\left( \widehat{BAD}+\widehat{ADB} \right) \\ & \Leftrightarrow \widehat{ABC}=\widehat{ABD} \\ \end{aligned} \)

(tổng ba góc trong một tam giác bằng \(180^o\))

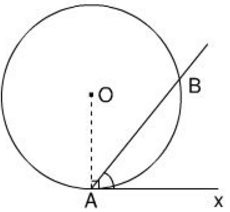
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).

Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.

Phương pháp giải

Kẻ OH vuông góc với AB.

Cần chứng minh \(Ax\bot OA.\)

Hướng dẫn giải

Vẽ \(OH\bot AB.\)

Trong tam giác vuông AOH  có:\( \widehat{OAH}+\widehat{AOH}={{90}^{o}} \)

Tam giác AOB cân tại O có OH là đường cao nên đồng thời là phân giác của góc AOB.

Suy ra \(\widehat{AOH}=\dfrac{1}{2}\widehat{AOB}=\dfrac{1}{2}\text{sđ}\overset\frown{AB} \)

Theo giả thiết ta lại có: \(\widehat{BAx}=\dfrac{1}{2}\text{sđ}\overset\frown{AB} \)

Nên \(\widehat{BAx}=\widehat{AOH} \)

Ta có: 

\(\widehat{OAx}=\widehat{OAB}+\widehat{BAx}=\widehat{OAB}+\widehat{AOH}={{90}^{o}} \)

Vậy OA vuông góc với \(Ax\) tại A nên \(Ax\) là tiếp tuyến của đường tròn O tại A.