Giải bài tập SGK Toán 9 Bài: Luyện tập
Dựa theo cấu trúc SGK Toán 9, eLib xin mời các em học sinh tham khảo giải bài tập bài Luyện tập trang 111, 112. Với các bài tập có lời giải chi tiết tương ứng với từng bài, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn.
Mục lục nội dung

1. Giải bài 8 trang 111 SGK Toán 9 tập 2
Cho hình chữ nhật ABCD (\(AB = 2a, BC = a\)). Quay hình chữ nhật đó quanh AB thì được hình trụ có thể tích \(V_1\); quanh BC thì được hình trụ có thể tích \(V_2\). Trong các đẳng thức dưới đây, hãy chọn đẳng thức đúng:
|
(A) \(V_1=V_2\) |
(B) \(V_1=2V_2\) |
(C) \(V_2=2V_1\) |
|
(D) \(V_2=3V_1\) |
(E) \(V_1=3V_2\) |
|
Phương pháp giải
Công thức tính thể tích hình trụ: \(V=S.h=\pi r^2h\)
Hướng dẫn giải
Quay hình chữ nhật ABCD xung quanh AB ta được hình trụ có chiều cao là 2a và bán kính đáy là a.
Ta có: \(V_1=\pi .a^2.2a=2\pi a^3\)
Quay hình chữ nhật ABCD quanh BC ta được hình trụ có chiều cao là a và bán kính đáy là 2a.
Suy ra \(V_2=\pi (2a)^2.a=4\pi a^3\)
Vậy \(V_2=2V_1\)
Chọn đáp án C.
2. Giải bài 9 trang 112 SGK Toán 9 tập 2
Hình 83 là một hình trụ cùng với hình khai triển của nó kèm theo kích thước.
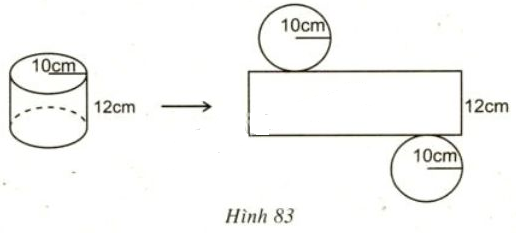
Hãy điền vào các chỗ ... và các ô trống những cụm từ hoặc các số cần thiết .
\(...:\,\,\,\square .\square .10=\square \,(cm^2)\\ ...:\,\,\,(2.\square .10).\square =\square \,\,(cm^2);\\ ...:\,\,\,\square .2+\square =\square \,\,(cm^2)\)
Phương pháp giải
Cho hình trụ có các kích thước: chiều cao là h, bán kính đáy là r. Khi đó ta có:
+) Diện tích một mặt đáy: \(S=\pi r^2.\)
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh+ 2\pi r^2.\)
+) Thể tích của hình trụ: \(V=Sh=\pi r^2 h.\)
Hướng dẫn giải
Điền vào ô trống:
Diện tích đáy: \(\pi.10.10=100\pi\,\,(cm^2)\)
Diện tích xung quanh: \((2.\pi.10).12=240\pi\,(cm^2)\)
Diện tích toàn phần: \(100\pi.2+240\pi=440\pi\,\,(cm^2)\)
3. Giải bài 10 trang 112 SGK Toán 9 tập 2
Hãy tính:
a) Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13cm và chiều cao là 3cm.
b) Thể tích của hình trụ có bán kính đường tròn đáy là 5mm và chiều cao là 8mm.
Phương pháp giải
Hình trụ có bán kính đáy r và chiều cao h, có:
- Diện tích xung quanh: \(S_{xq}=2\pi rh\)
- Thể tích: \(V=Sh=\pi r^2h\)
Hướng dẫn giải
a) Diện tích của hình trụ là:
\(S_{xq}=2\pi rh=Ch=13.3=39\,\,(cm^2)\)
b) Thể tích hình trụ là:
\(V=\pi r^2 h=\pi.5^2.8=200\pi\,\,(cm^2)\)
4. Giải bài 11 trang 112 SGK Toán 9 tập 2
Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào một lọ thủy tinh có nước dạng hình trụ (h.84). Diện tích đáy lọ thủy tinh là \(12,8cm^2\). Nước trong lọ dâng lên thêm 8,5mm. Hỏi thể tích của tượng đá là bao nhiêu?
Phương pháp giải
Phần thể tích nước nâng lên là thể tích của tượng đá.
Công thức thể tích của hình trụ: \(V=Sh=\pi r^2h.\)
Hướng dẫn giải
Thể tích của tượng đá bằng thể tích của hình trụ có diện tích đáy là \(12,8cm^2\) và chiều cao là \(8,5mm=0,85cm\)
\(V=12,8.0,85=10,88\,cm^3\)
5. Giải bài 12 trang 112 SGK Toán 9 tập 2
Điền đủ các kết quả vào những ô trống của bảng sau:

Phương pháp giải
Hình trụ có diện tích đáy r và chiều cao h thì có:
- Đường kính đáy \(d=2r.\)
- Chu vi đáy: \(C=2\pi r=\pi d\)
- Diện tích đáy: \(S=\pi r^2\)
- Diện tích xung quanh: \(S_{xq}=2\pi r h\)
- Thể tích: \(V=\pi r^2h\)
- Biểu diễn chiều cao h: \(h=\dfrac{V}{S}=\dfrac{S_{xq}}{C}\)
Hướng dẫn giải
Đổi 25mm = 2,5cm; 1m = 100cm; 1l = 1000cm3
+ Khi r = 2,5cm; h = 7cm thì hình trụ có
- Đường kính d = 2r = 2.2,5 = 5cm
- Chu vi đáy \(C = 2\pi r = 2.\pi .2,5 = 5\pi \left( {cm} \right)\)
- Diện tích đáy \(S = \pi {r^2} = \pi .2,{5^2} = 6,25\pi \left( {c{m^2}} \right)\)
- Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .2,5.7 = 35\pi \left( {c{m^2}} \right)\)
- Thể tích \(V = \pi {r^2}h = \pi .2,{5^2}.7 = 43,75\pi \left( {c{m^3}} \right)\)
+ Khi d = 6cm; h = 100cm thì hình trụ có
- Bán kính \(r = \dfrac{d}{2} = \dfrac{6}{2} = 3cm\)
- Chu vi đáy \(C = 2\pi r = 2.\pi .3 = 6\pi \left( {cm} \right)\)
- Diện tích đáy \(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
- Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .3.100 = 100\pi \left( {c{m^2}} \right)\)
- Thể tích \(V = \pi {r^2}h = \pi {.3^2}.100 = 900\pi \left( {c{m^3}} \right)\)
+ Khi r = 5cm; V = 1000cm3 thì hình trụ có
- Đường kính d = 2r = 2.5 = 10cm
- Chu vi đáy \(C = 2\pi r = 2.\pi .5 = 10\pi \left( {cm} \right)\)
- Diện tích đáy \(S = \pi {r^2} = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\)
- Chiều cao \(h = \dfrac{V}{{\pi {r^2}}} = \dfrac{{1000}}{{\pi {{.5}^2}}} = \dfrac{{40}}{\pi }\left( {cm} \right)\)
- Diện tích xung quanh \({S_{xq}} = 2\pi rh = 2\pi .5.\dfrac{{40}}{\pi } = 400\left( {c{m^2}} \right)\)
Ta có bảng sau:
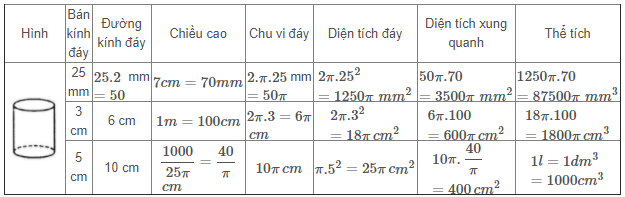
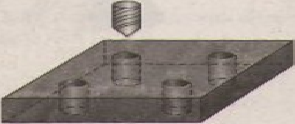
6. Giải bài 13 trang 113 SGK Toán 9 tập 2
Một tấm kim loại được khoan thủng bốn lỗ như hình 85 (lỗ khoan dạng hình trụ),tấm kim loại dày 2cm, đáy của nó là hình vuông cạnh là 5 cm. Đường kính của mũi khoan là 8 mm. Hỏi thể tích phần còn lại của tấm kim loại là bao nhiêu?
Phương pháp giải
- Ta có các công thức
Cho hình trụ có các kích thước: chiều cao là h, bán kính đáy là r. Thì thể tích của hình trụ: \(V=Sh=\pi r^2 h.\)
Thể tích hình hộp chữ nhật có 3 kích thước a; b; c là V=abc
- Thực hiện các phép tính
+ Tính thể tích miếng kim loại.
+ Tính thể tích của 4 lỗi khoan.
+ Tính thể tích phần còn lại.
Hướng dẫn giải
Thể tích của miếng kim loại là:
\(V_2=S.h=5^2.2=50\,cm^3=50000\,mm^3\)
Thể tích của 4 lỗ khoan là:
\(V_1=4.\pi.4^2.20=1280\pi\approx4019\,mm^3\)
Vậy thể tích còn lại là
\(V=50000-4019=45981\,mm^3\)
7. Giải bài 14 trang 113 SGK Toán 9 tập 2
Đường ống nối hai bể cá trong một thủy cung ở miền nam nước Pháp có dạng một hình trụ, độ dài của đường ống là 30m (h.86). Dung tích của đường ống nói trên là 1 800 000 lít.
Tính diện tích đáy của đường ống.
Phương pháp giải
- Cho hình trụ có các kích thước: chiều cao là \(h,\) bán kính đáy là r. Khi đó:
Thể tích của hình trụ là: \(V=Sh=\pi r^2 h\)
- Dung tích của bình là thể tích tối đa bình có thể chứa. Ở đây muốn chỉ thể tích của đường ống hình trụ là 1 800 000 lít
Hướng dẫn giải
Chiều dài đường ống là \(30m=300dm\) và thể tích đường ống bằng 1 800 000 lít \(=\) 1 800 000 \(dm^3\)
Diện tích đáy của đường ống là:
\(1800000:300=6000\,dm^2\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 9 Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ
- doc Giải bài tập SGK Toán 9 Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 3: Hình cầu. Diện tích hình cầu và thể tích hình cầu
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập