Giải bài tập SGK Toán 9 Bài: Luyện tập
Mời các em học sinh lớp 9 cùng tham khảo nội dung giải bài tập SGK bài Luyện tập trang 116 dưới đây. Bài gồm có 3 bài tập được eLib sưu tầm và tổng hợp. Với nội dung chi tiết, rõ ràng giúp các em ôn tập lại các kiến thức đã học và vận dụng vào giải các bài tập tương tự. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy của quý thầy cô và học tập của các em học sinh.
Mục lục nội dung

1. Giải bài 30 trang 116 SGK Toán 9 tập 1
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
a) \(\widehat{COD}={{90}^{o}}\)
b) \(CD = AC + BD\)
c) Tích \(AC.BD\) không đổi khi điểm M di chuyển trên nửa đường tròn.
Phương pháp giải
- Sử dụng tính chất hai đường tiếp tuyến cắt nhau: AB, AC là tiếp tuyến của (O) tại A, B thì AB=AC; OA là tia phân giác của góc \(\widehat{BOC}\)
Sử dụng hệ thức lượng trong tam giác vuông: \(\Delta{ABC}\) vuông tại A, đường cao AH. Khi đó \(AH^2=HB.HC\)
Hướng dẫn giải
a) Ta có: \(\left\{ \begin{aligned} & \widehat{AOC}=\widehat{MOC} \\ & \widehat{BOD}=\widehat{MOD} \\ \end{aligned} \right.\) (tính chất hai tiếp tuyến cắt nhau)
Mà \(\widehat{AOB}=\widehat{AOM}+\widehat{BOM}={{180}^{o}}\) (hai góc kề bù)
\(\Rightarrow \widehat{COD}=\widehat{COM}+\widehat{DOM}=\dfrac{1}{2}\widehat{AOB}={{90}^{o}}\)
b) Ta có: \(\left\{ \begin{aligned} & AC=CM \\ & BD=DM \\ \end{aligned} \right.\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra \(CD=CM+DM=AC+BD\)
c) Ta có \(OM\bot CD\) (tính chất tiếp tuyến)
Xét tam giác vuông COD, đường cao OM, ta có:
\(MC.MD=OM^2\) (hệ thức lượng trong tam giác vuông)
Suy ra \(AC.BD=OM^2\)
Mà OM không đổi nên tích \(AC.BD\) không đổi.
2. Giải bài 31 trang 116 SGK Toán 9 tập 1
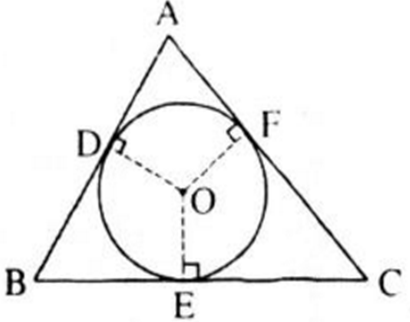
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
a) Chứng minh rằng: \(2AD = AB + AC - BC\)
b) Tìm các hệ thức tương tự như hệ thức ở câu a).
Phương pháp giải
- Sử dụng tính chất hai tiếp tuyến cắt nhau để chứng minh các đoạn thẳng bằng nhau: Nếu AB, AC là hai tiếp tuyến của (O) lần lượt tại A, B thì ta có: AB=AC
- Chu vi tam giác ABC là \(C_{\Delta{ABC}}=AB+AC+BC\)
Hướng dẫn giải
Ta có: \(\left\{ \begin{aligned} & BD=BE \\ & CE=CF \\ & AD=AF \\ \end{aligned} \right.\) (tính chất của hai tiếp tuyến cắt nhau)
Suy ra
\( \begin{align} AB+AC-BC&=\left( AD+BD \right)+\left( AF+FC \right)-\left( BE+EC \right) \\ &=\left( AD+AF \right)+\left( DB-BE \right)+\left( FC-EC \right) \\ &=AD+AF=2AD. \\ \end{align} \)
Vậy \(2AD = AB + AC - BC\)
b) Tương tự ta tìm được các hệ thức:
\(2BE = BA + BC - AC\\ 2CF = CA + CB - AB\)
3. Giải bài 32 trang 116 SGK Toán 9 tập 1
Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:
\(\left( A \right)\,6c{{m}^{2}}\);
\(\,\left( B \right)\,\sqrt{3}\,c{{m}^{2}}\);
\(\left( C \right)\dfrac{3\sqrt{3}}{4}c{{m}^{2}}\);
\(\left( D \right)3\sqrt{3}c{{m}^{2}}\).
Hãy chọn câu trả lời đúng.
Phương pháp giải
+) Sử dụng tính chất: Trong tam giác đều, đường cao đồng thời là đường trung tuyến.
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: \(\Delta{ABC}\) vuông tại A. Khi đó: \(AB=BC. \sin C;\ AC=BC. \sin B\)
+) Công thức tính diện tích tam giác: \(S=\dfrac{1}{2}.h.a\)
trong đó h là độ dài đường cao, a là độ dài cạnh ứng với đường cao.
Hướng dẫn giải
Gọi O là tâm đường tròn nội tiếp \(Δ ABC\), H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên \(A, O, H\) thẳng hàng.
Ta có: \(HB = HC, \widehat{HAC}={{30}^{o}}\)
Do tam giác ABC đều nên O cũng là trọng tâm tam giác.
Suy ra \(AH = 3.OH = 3 (cm)\)
Trong tam giác vuông HAC, có
\(HC=AH.tg30^o=3.\dfrac{\sqrt{3}}{3}=\sqrt{3}\,\left( cm \right)\)
Diện tích tam giác ABC là:
\(S=\dfrac{1}{2}AH.BC=AH.HC=3.\sqrt{3}=3\sqrt{3}\,\left( c{{m}^{2}} \right)\)
Chọn D.
Tham khảo thêm
- doc Giải bài tập SGK Toán 9 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 2: Đường kính và dây của đường tròn
- doc Giải bài tập SGK Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- doc Giải bài tập SGK Toán 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- doc Giải bài tập SGK Toán 9 Bài 7: Vị trí tương đối của hai đường tròn
- doc Giải bài tập SGK Toán 9 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Ôn tập chương 2: Đường tròn