Giải bài tập SGK Toán 9 Bài 3 Góc nội tiếp
Dưới đây là hướng dẫn giải bài tập SGK Toán 9 Bài Góc nội tiếp trang 75 với nội dung gồm 4 bài tập có hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. eLib hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 9 học tập thật tốt.
Mục lục nội dung

1. Giải bài 15 trang 75 SGK Toán 9 tập 2
Các khẳng định sau đúng hay sai?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.
Phương pháp giải
Hệ quả:
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng \({90^0}\)) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Hướng dẫn giải
a) Đúng (theo hệ quả b: Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau)
b) Sai, vì trong một đường tròn các góc nội tiếp bằng nhau có thể là chắn các cung bằng nhau hoặc cùng chắn một cung.
2. Giải bài 16 trang 75 SGK Toán 9 tập 2
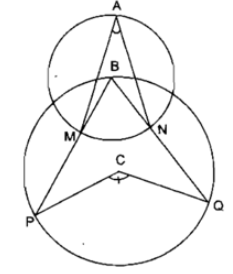
Xem hình 19 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C)
a) Biết \(\widehat{MAN}=30^o\), tính \(\widehat{PCQ}\)
b) Nếu \(\widehat{PCQ}=136^o\), thì \(\widehat{MAN}\) có số đo là bao nhiêu?
Phương pháp giải
a) Trong đường tròn (B), góc MAN là góc nội tiếp chắn cung MN nên:
\(\widehat{MAN}=\dfrac 1 2 \widehat{MBN}\)
Trong đường tròn (C), góc MBN là góc nội tiếp chắn cung PQ nên
\(\widehat{MBN}=\dfrac 1 2 \widehat{PCQ}\)
b) Trong đường tròn (C), góc MBN là góc nội tiếp chắn cung PQ nên
\(\widehat{MBN}=\dfrac 1 2. \widehat{PCQ}\)
Trong đường tròn (B), góc MAN là góc nội tiếp chắn cung MN nên:
\(\widehat{MAN}=\dfrac 1 2 .\widehat{MBN}\)
Hướng dẫn giải
a) \(\widehat{MAN}=30^o\)
Trong đường tròn (B), góc MAN là góc nội tiếp chắn cung MN nên:
\(\widehat{MAN}=\dfrac 1 2 \widehat{MBN}\\ \Rightarrow \widehat{MBN}=2.30^o=60^o\)
Trong đường tròn (C), góc MBN là góc nội tiếp chắn cung PQ nên
\(\widehat{MBN}=\dfrac 1 2 \widehat{PCQ}\\ \Rightarrow \widehat{PCQ}=2.60^o=120^o\)
b) \(\widehat{PCQ}=136^o\)
Trong đường tròn (C), góc MBN là góc nội tiếp chắn cung PQ nên
\(\widehat{MBN}=\dfrac 1 2. \widehat{PCQ}=\dfrac{136^o} 2=68^o\)
Trong đường tròn (B), góc MAN là góc nội tiếp chắn cung MN nên:
\(\widehat{MAN}=\dfrac 1 2 .\widehat{MBN}=\dfrac{68^o}{2}=34^o\)
3. Giải bài 17 trang 75 SGK Toán 9 tập 2
Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?
Phương pháp giải
Sử dụng:
+ Các góc nội tiếp chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông
Hướng dẫn giải
Cách xác định:
+ Đặt đỉnh vuông của eke trùng với một điểm N bất kỳ trên đường tròn, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại A và B ta được đường kính AB.
+ Vẫn đặt đỉnh vuông của eke tại N, xoay eke theo hướng khác, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại C và D ta được đường kính CD.
+ CD cắt AB tại tâm O của đường tròn.
4. Giải bài 18 trang 75 SGK Toán 9 tập 2
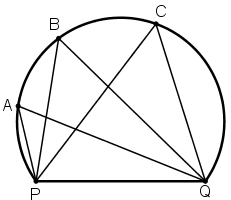
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20.
Hãy so sánh các góc \(\widehat{PAQ},\widehat{PBQ},\widehat{PCQ}\)
Phương pháp giải
Trong một đường tròn:
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Hướng dẫn giải
Vì A, B, C là các điểm thuộc cung tròn PQ nên các góc \(\widehat{PAQ},\widehat{PBQ},\widehat{PCQ}\) là các góc nội tiếp cùng chắn cung PQ.
Suy ra \(\widehat{PAQ}=\widehat{PBQ}=\widehat{PCQ}\) (các góc nội tiếp cùng chắn một cung thì bằng nhau)
Tham khảo thêm
- doc Giải bài tập SGK Toán 9 Bài 1: Góc ở tâm. Số đo cung
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 2: Liên hệ giữa cung và dây
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập
- doc Giải bài tập SGK Toán 9 Bài 6: Cung chứa góc
- doc Giải bài tập SGK Toán 9 Bài: Luyện tập